第九章 图形的相似 综合练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
综合练习
一、选择题
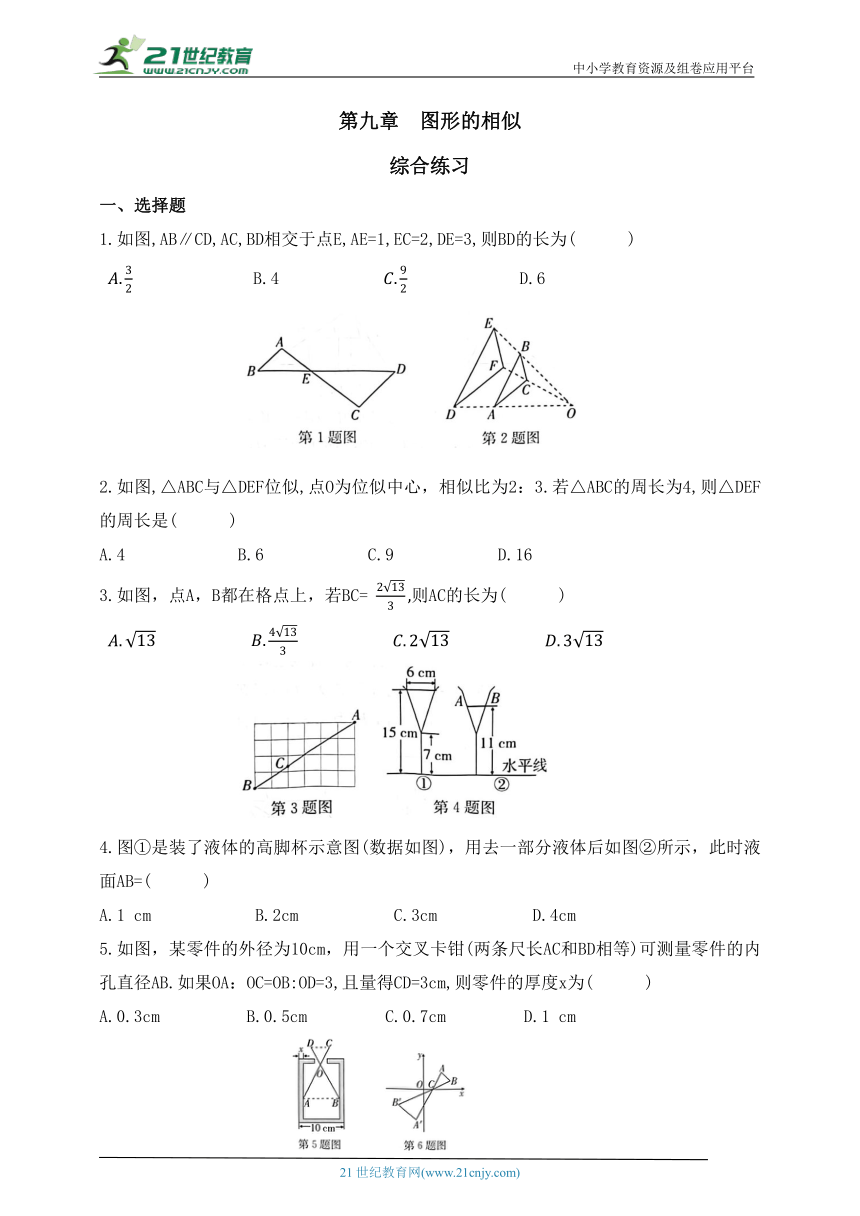
1.如图,AB∥CD,AC,BD相交于点E,AE=1,EC=2,DE=3,则BD的长为( )
B.4 D.6
2.如图,△ABC与△DEF位似,点O为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )
A.4 B.6 C.9 D.16
3.如图,点A,B都在格点上,若BC= 则AC的长为( )
4.图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB=( )
A.1 cm B.2cm C.3cm D.4cm
5.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( )
A.0.3cm B.0.5cm C.0.7cm D.1 cm
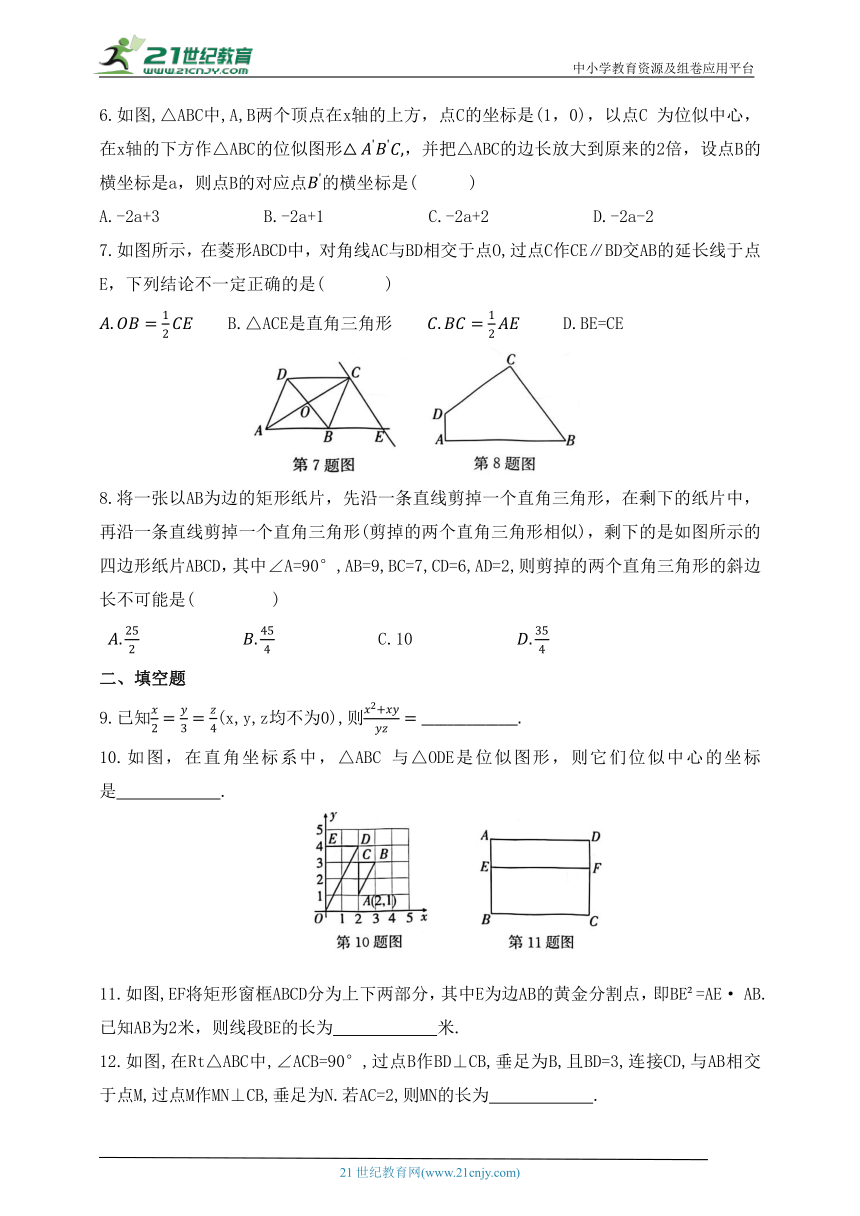
6.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C 为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A.-2a+3 B.-2a+1 C.-2a+2 D.-2a-2
7.如图所示,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是( )
B.△ACE是直角三角形 D.BE=CE
8.将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
C.10
二、填空题
9.已知(x,y,z均不为0),则
10.如图,在直角坐标系中,△ABC 与△ODE是位似图形,则它们位似中心的坐标是 .
11.如图,EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即BE =AE· AB. 已知AB为2米,则线段BE的长为 米.
12.如图,在Rt△ABC中,∠ACB=90°,过点B作BD⊥CB,垂足为B,且BD=3,连接CD,与AB相交于点M,过点M作MN⊥CB,垂足为N.若AC=2,则MN的长为 .
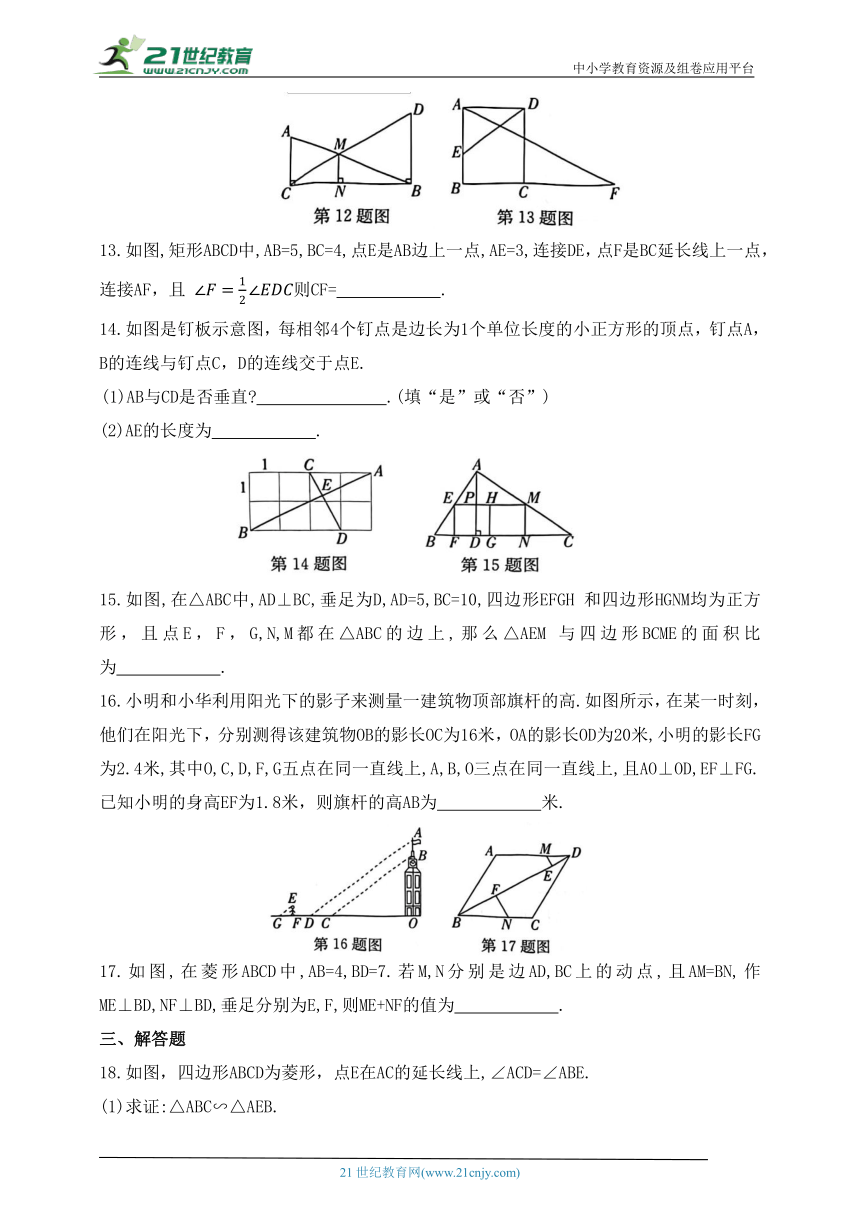
13.如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且 则CF= .
14.如图是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形的顶点,钉点A,B的连线与钉点C,D的连线交于点E.
(1)AB与CD是否垂直 .(填“是”或“否”)
(2)AE的长度为 .
15.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH 和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM 与四边形BCME的面积比为 .
16.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O,C,D,F,G五点在同一直线上,A,B,O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,则旗杆的高AB为 米.
17.如图,在菱形ABCD中,AB=4,BD=7.若M,N分别是边AD,BC上的动点,且AM=BN,作ME⊥BD,NF⊥BD,垂足分别为E,F,则ME+NF的值为 .
三、解答题
18.如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB.
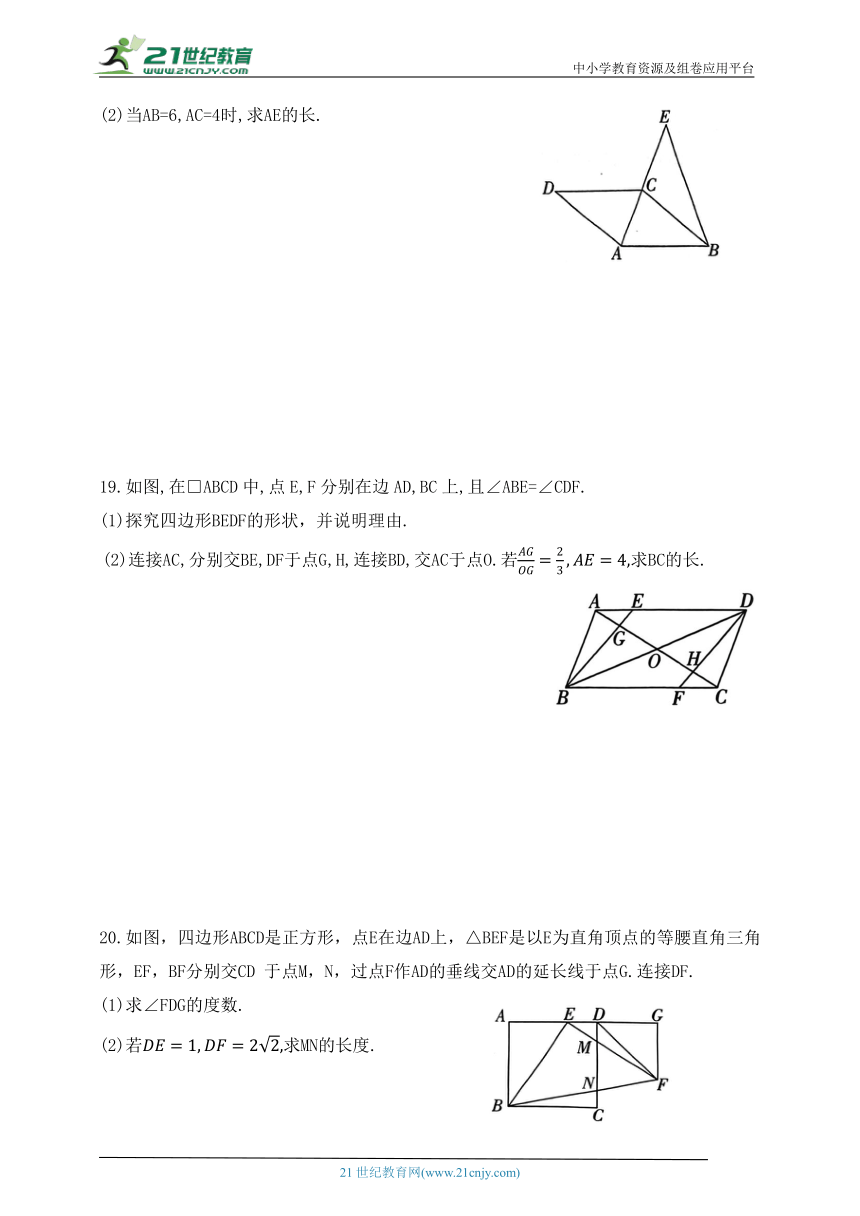
(2)当AB=6,AC=4时,求AE的长.
19.如图,在□ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由.
(2)连接AC,分别交BE,DF于点G,H,连接BD,交AC于点O.若求BC的长.
20.如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD 于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF.
(1)求∠FDG的度数.
(2)若求MN的长度.
21.如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC.
(2)找出图中与△OBF相似的三角形,并说明理由.
(3)若OF=3,EF=2,求DE的长度.
参考答案
1.C 2.B 3.B 4.C 5.B 6.A 7.D
8.A [解析]如图①所示,由已知可得△DFE∽△ECB,则 .
设DF=x,CE=y,则解得故B不符合题意: 故D不符合题意.
如图②所示,由已知可得△DCF∽△FEB,则
设FC=m,FD=n,则解得=10,故C不符合题意;
BF=FC+BC=8+7=15,故选A.
10.(4,2)
13.6 [解析]如图,连接EC,过点D作DH⊥EC于点H.
∵四边形ABCD是矩形,∴∠BAD=∠BCD=90°,AD =BC= 4,AB=CD =5.
∵AE=3,∴DE=
∠DCH+∠CDH=90°,∴∠BCE=∠CDH,∴∠BCE
∥ 即
14.(1)是
[解析](1)如图①,在△ACM和△CFD中 (SAS),
∴∠CAM=∠FCD.∵∠CAM+∠CMA=90°,∴∠FCD+∠CMA=90°,
∴∠CEM=90°,∴AB⊥CD.
(2)如图②,在Rt△ABH中,
∥
15.1:3 [解析]∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,∴△AEM∽△ABC,
即
∴△AEM与四边形BCME的面积比为1:3.
16.3
[解析]如图,连接AC交BD于点O.∵四边形ABCD为菱形,
OA=OC.
由勾股定理得
即 解得
同理可得NF=
18.(1)证明:∵四边形ABCD为菱形,∴∠ACD=∠BCA.
∵∠ACD=∠ABE,∴∠BCA=∠ABE.
∵∠BAC=∠EAB,∴△ABC∽△AEB.
(2)解:∵△ABC∽
19.解:(1)四边形BEDF为平行四边形.
理由:∵四边形ABCD为平行四边形,∴∠ABC=∠ADC.
∵∠ABE=∠CDF,∴∠EBF=∠EDF.
∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EDF=∠DFC=∠EBF,∴BE∥DF,
∴四边形BEDF为平行四边形.
(2)设
∵四边形ABCD为平行四边形,∴AO=CO=5a,AC=10a,CG=8a.
∵AD∥BC, =16.
20.解:∵△BEF是以E为直角顶点的等腰直角三角形,∴∠AEB+∠GEF=90°.
∵∠AEB+∠ABE=90°,∴∠GEF=∠ABE.
在△ABE和△GEF中,
∴EG=AB=AD,GF=AE,即DG+DE=AE+DE,∴DG=AE,
∴DG=GF,即△DGF是等腰直角三角形,∴∠FDG=45°.
由(1)知△DGF是等腰直角三角形,
∴DG=GF=2,AB=AD=CD=ED+DG=2+1=3.
如图,延长GF交BC的延长线于点H,则
∴ 即
同理,△BNC∽△BFH, 即
21.(1)证明:如图,在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,
∴∠2=∠3=∠4,∠3+∠5=90°.∵DE=BE,∴∠1=∠2.
又∵BE平分∠DBC,∴∠1=∠6,∴∠3=∠6,∴∠6+∠5=90°,∴BF⊥AC.
(2)解:与△OBF相似的三角形有△ECF,△BAF.
理由如下:由(1)可得∠1=∠4=∠3.
∵∠BFO=∠AFB,∴△BAF ∽△OBF.
∵∠1=∠3,∠EFC=∠BFO,∴△ECF∽△OBF.
(3)解: 即
∴BF =3(OA+3)②.
联立①②,可得 (负值舍去),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
综合练习
一、选择题
1.如图,AB∥CD,AC,BD相交于点E,AE=1,EC=2,DE=3,则BD的长为( )
B.4 D.6
2.如图,△ABC与△DEF位似,点O为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )
A.4 B.6 C.9 D.16
3.如图,点A,B都在格点上,若BC= 则AC的长为( )
4.图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB=( )
A.1 cm B.2cm C.3cm D.4cm
5.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为( )
A.0.3cm B.0.5cm C.0.7cm D.1 cm
6.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C 为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A.-2a+3 B.-2a+1 C.-2a+2 D.-2a-2
7.如图所示,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是( )
B.△ACE是直角三角形 D.BE=CE
8.将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
C.10
二、填空题
9.已知(x,y,z均不为0),则
10.如图,在直角坐标系中,△ABC 与△ODE是位似图形,则它们位似中心的坐标是 .
11.如图,EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即BE =AE· AB. 已知AB为2米,则线段BE的长为 米.
12.如图,在Rt△ABC中,∠ACB=90°,过点B作BD⊥CB,垂足为B,且BD=3,连接CD,与AB相交于点M,过点M作MN⊥CB,垂足为N.若AC=2,则MN的长为 .
13.如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且 则CF= .
14.如图是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形的顶点,钉点A,B的连线与钉点C,D的连线交于点E.
(1)AB与CD是否垂直 .(填“是”或“否”)
(2)AE的长度为 .
15.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH 和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM 与四边形BCME的面积比为 .
16.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O,C,D,F,G五点在同一直线上,A,B,O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,则旗杆的高AB为 米.
17.如图,在菱形ABCD中,AB=4,BD=7.若M,N分别是边AD,BC上的动点,且AM=BN,作ME⊥BD,NF⊥BD,垂足分别为E,F,则ME+NF的值为 .
三、解答题
18.如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB.
(2)当AB=6,AC=4时,求AE的长.
19.如图,在□ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由.
(2)连接AC,分别交BE,DF于点G,H,连接BD,交AC于点O.若求BC的长.
20.如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD 于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF.
(1)求∠FDG的度数.
(2)若求MN的长度.
21.如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC.
(2)找出图中与△OBF相似的三角形,并说明理由.
(3)若OF=3,EF=2,求DE的长度.
参考答案
1.C 2.B 3.B 4.C 5.B 6.A 7.D
8.A [解析]如图①所示,由已知可得△DFE∽△ECB,则 .
设DF=x,CE=y,则解得故B不符合题意: 故D不符合题意.
如图②所示,由已知可得△DCF∽△FEB,则
设FC=m,FD=n,则解得=10,故C不符合题意;
BF=FC+BC=8+7=15,故选A.
10.(4,2)
13.6 [解析]如图,连接EC,过点D作DH⊥EC于点H.
∵四边形ABCD是矩形,∴∠BAD=∠BCD=90°,AD =BC= 4,AB=CD =5.
∵AE=3,∴DE=
∠DCH+∠CDH=90°,∴∠BCE=∠CDH,∴∠BCE
∥ 即
14.(1)是
[解析](1)如图①,在△ACM和△CFD中 (SAS),
∴∠CAM=∠FCD.∵∠CAM+∠CMA=90°,∴∠FCD+∠CMA=90°,
∴∠CEM=90°,∴AB⊥CD.
(2)如图②,在Rt△ABH中,
∥
15.1:3 [解析]∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,∴△AEM∽△ABC,
即
∴△AEM与四边形BCME的面积比为1:3.
16.3
[解析]如图,连接AC交BD于点O.∵四边形ABCD为菱形,
OA=OC.
由勾股定理得
即 解得
同理可得NF=
18.(1)证明:∵四边形ABCD为菱形,∴∠ACD=∠BCA.
∵∠ACD=∠ABE,∴∠BCA=∠ABE.
∵∠BAC=∠EAB,∴△ABC∽△AEB.
(2)解:∵△ABC∽
19.解:(1)四边形BEDF为平行四边形.
理由:∵四边形ABCD为平行四边形,∴∠ABC=∠ADC.
∵∠ABE=∠CDF,∴∠EBF=∠EDF.
∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EDF=∠DFC=∠EBF,∴BE∥DF,
∴四边形BEDF为平行四边形.
(2)设
∵四边形ABCD为平行四边形,∴AO=CO=5a,AC=10a,CG=8a.
∵AD∥BC, =16.
20.解:∵△BEF是以E为直角顶点的等腰直角三角形,∴∠AEB+∠GEF=90°.
∵∠AEB+∠ABE=90°,∴∠GEF=∠ABE.
在△ABE和△GEF中,
∴EG=AB=AD,GF=AE,即DG+DE=AE+DE,∴DG=AE,
∴DG=GF,即△DGF是等腰直角三角形,∴∠FDG=45°.
由(1)知△DGF是等腰直角三角形,
∴DG=GF=2,AB=AD=CD=ED+DG=2+1=3.
如图,延长GF交BC的延长线于点H,则
∴ 即
同理,△BNC∽△BFH, 即
21.(1)证明:如图,在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,
∴∠2=∠3=∠4,∠3+∠5=90°.∵DE=BE,∴∠1=∠2.
又∵BE平分∠DBC,∴∠1=∠6,∴∠3=∠6,∴∠6+∠5=90°,∴BF⊥AC.
(2)解:与△OBF相似的三角形有△ECF,△BAF.
理由如下:由(1)可得∠1=∠4=∠3.
∵∠BFO=∠AFB,∴△BAF ∽△OBF.
∵∠1=∠3,∠EFC=∠BFO,∴△ECF∽△OBF.
(3)解: 即
∴BF =3(OA+3)②.
联立①②,可得 (负值舍去),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
