第九章《图形的相似》综合检测题(含答案)
文档属性
| 名称 | 第九章《图形的相似》综合检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 18:35:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章综合检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
1.若a:b=3:4,且a+b=14,则2a-b的值是( )
A.4 B.2 C.20 D.14
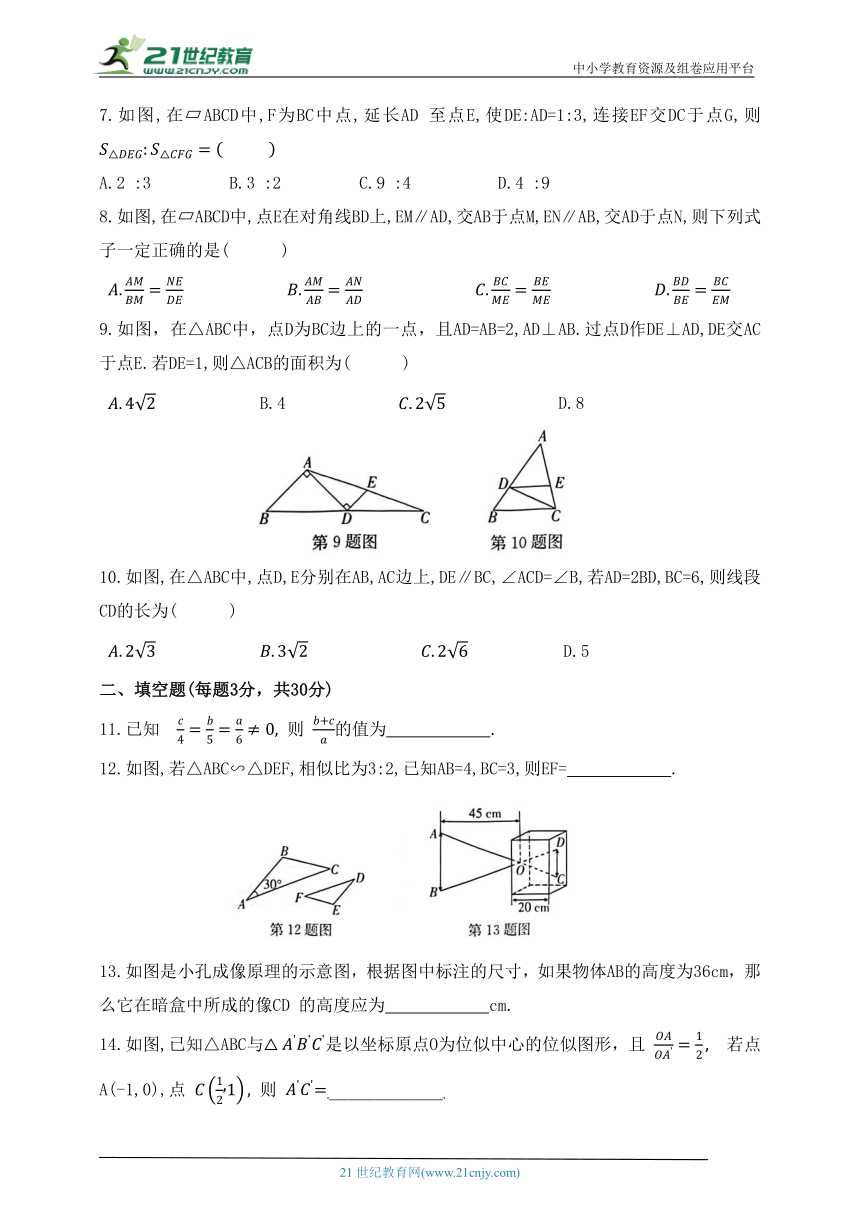
2.如图,AD∥BE∥CF,直线l ,l 与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
3.如图,在△ABC中,两条中线BE,CD相交于点O,则
A.1 :4 B.2 :3 C.1 :3 D.1 :2
4.如图,△OAB与位似,其中A,B的对应点分别为 均在图中正方形网格格点上,若线段AB上有一点P(m,n),则点P在上的对应点的坐标为( )
B.(m,n) C.(2m,2n) D.(2n,2m)
5.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )
A.1
6.如图,已知在△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列条件后,仍无法判定△ABC∽△DAE的是( )
B.∠B=∠D C.AD∥BC D.∠BAC=∠D
7.如图,在 ABCD中,F为BC中点,延长AD 至点E,使DE:AD=1:3,连接EF交DC于点G,则
A.2 :3 B.3 :2 C.9 :4 D.4 :9
8.如图,在 ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
9.如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ACB的面积为( )
B.4 D.8
10.如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
D.5
二、填空题(每题3分,共30分)
11.已知 则 的值为 .
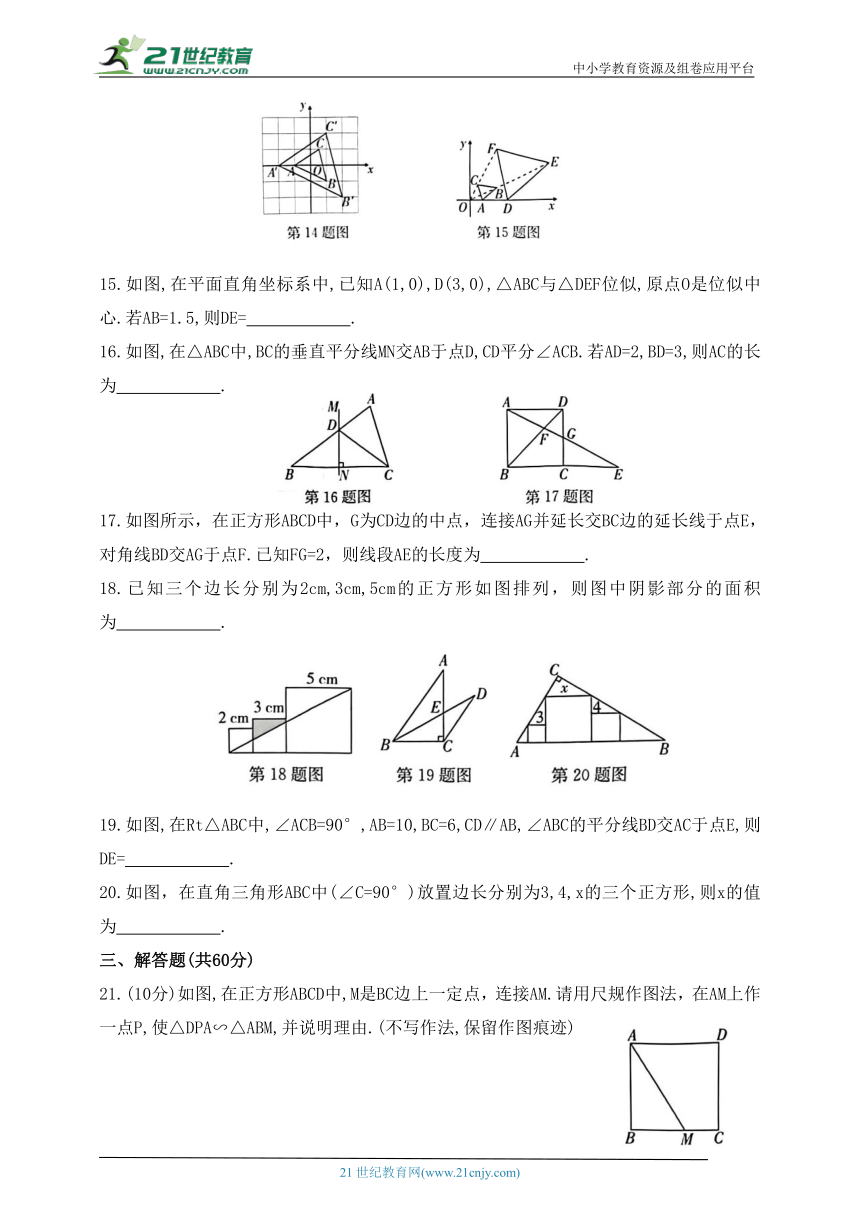
12.如图,若△ABC∽△DEF,相似比为3:2,已知AB=4,BC=3,则EF= .
13.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD 的高度应为 cm.
14.如图,已知△ABC与是以坐标原点O为位似中心的位似图形,且 若点A(-1,0),点 则
15.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
16.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .
17.如图所示,在正方形ABCD中,G为CD边的中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F.已知FG=2,则线段AE的长度为 .
18.已知三个边长分别为2cm,3cm,5cm的正方形如图排列,则图中阴影部分的面积为 .
19.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,则DE= .
20.如图,在直角三角形ABC中(∠C=90°)放置边长分别为3,4,x的三个正方形,则x的值为 .
三、解答题(共60分)
21.(10分)如图,在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM,并说明理由.(不写作法,保留作图痕迹)
22.(12分)在如图所示的平面直角坐标系中,已知点A(-3,-3),点B(-1,-3),点C(-1,-1).
(1)画出△ABC.
(2)画出△ABC关于x轴对称的△A B C ,并写出A 点的坐标: .
(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到 △A B C ,画出△A B C ,并写出A 点的坐标: .
23.(12分)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.
(2)若AB=13,BC=10,求线段DE的长.
24.(12分)如图,矩形ABCD中,点E是AB的中点,过点E 作CE的垂线,交CD的延长线于点G,交AD于点F,且点F是AD的中点.
(1)求证:△EBC∽△CEG.
(2)求证:
25.(14分)已知:△ABC中,∠BAC=90°,AB=AC,D为BC 的中点,F,E是AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
(1)如图①,求证:∠FDC=∠AEB.
(2)如图①,若AE=3CE=6,求BG的长.
(3)如图②,若F为AC上任意一点,连接AG.
求证:∠EAG=∠ABE.
参考答案
1.A 2.B 3.A 4.C 5.C 6.B 7.D 8.D
9.B [解析]∵AB⊥AD,AD⊥DE,∴∠BAD=∠ADE=90°,∴DE∥AB,∴∠CED=∠CAB.
∵∠C=∠C,∴△CED∽△CAB.
∵DE=1,AB=2,即DE:AB=
10.C [解析]设AD=2x,则BD=x,AB=3x.
∵DE∥BC,
∴∠ADE=∠ACD.∵∠A=∠A,∴△ADE∽△ACD,
设
12.2 13.16 15.4.5 17.12
18.3.75cm [解析]根据相似的性质可知 解得x=2.5,
∴阴影梯形的上底是3-2.5=0.5(cm).
再根据相似的性质可知 解得y=1,∴梯形的下底是3-1=2(cm),
∴阴影梯形的面积是(0.5+2)×3÷2=3.75( cm ).
[解析]∵∠ACB=90°,AB=10,BC=6,∴AC=8.
∵BD平分∠ABC,∴∠ABE=∠CBE.∵CD∥AB,∴∠D=∠ABE,∴∠D=∠CBE,∴CD=BC=6,
∴CE
20.7
21.解:如图所示,点P即为所求.
理由:∵DP⊥AM,∴∠APD=∠ABM=90°.
∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA ∽△ABM.
22.解:(1)图略. (2)图略.(-3,3) (3)图略.(6,6)
23.(1)证明:∵AD为BC边上的中线,∴BD=CD.
∵AB=AC,∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,∴△BDE∽△CAD.
(2)解:在Rt△ADB中,
∴AD=
24.证明:(1)∵CE⊥EG,∴∠GEC=90°.
∵四边形ABCD是矩形,∴∠EBC=90°,AB∥CD,
∴∠BEC=∠ECG.
(2)∵E,F分别是AB,AD的中点,∴EF是△ABD的中位线,
∠DFG,AF=DF,∴△AFE≌△DFG(AAS),∴GF=
∵四边形ABCD是矩形,∴∠ADC=90° ,∴∠ADG=180°- ∠ADC =90°,∴∠GDF=∠GEC.
∵∠G=∠G,∴△GFD∽△GCE,
25.(1)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠C=45°.
∵∠BGD=∠EGF=45° ,∴∠BGD=∠C.
∵∠FDC=∠EBC+∠BGD,∠AEB=∠EBC+∠C,∴∠FDC=∠AEB.
(2)解:∵AE=3CE=6,∴CE=2,AE=6,∴AB=AC=8.
∵∠A=90°,∴BE=
D 是BC的中点,
即
(3)证明:如图,连接AD.∵AB=AC,D为BC的中点,∴AD⊥BC,∴∠ADB=90°=∠BAC.
∴AB =BD · BC.
由(2)知△
∴∠AGB=∠BAE=90°,∴∠EAG+∠BAG=∠BAG+∠ABE=90°,∴∠EAG=∠ABE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章综合检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
1.若a:b=3:4,且a+b=14,则2a-b的值是( )
A.4 B.2 C.20 D.14
2.如图,AD∥BE∥CF,直线l ,l 与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
3.如图,在△ABC中,两条中线BE,CD相交于点O,则
A.1 :4 B.2 :3 C.1 :3 D.1 :2
4.如图,△OAB与位似,其中A,B的对应点分别为 均在图中正方形网格格点上,若线段AB上有一点P(m,n),则点P在上的对应点的坐标为( )
B.(m,n) C.(2m,2n) D.(2n,2m)
5.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )
A.1
6.如图,已知在△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列条件后,仍无法判定△ABC∽△DAE的是( )
B.∠B=∠D C.AD∥BC D.∠BAC=∠D
7.如图,在 ABCD中,F为BC中点,延长AD 至点E,使DE:AD=1:3,连接EF交DC于点G,则
A.2 :3 B.3 :2 C.9 :4 D.4 :9
8.如图,在 ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
9.如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ACB的面积为( )
B.4 D.8
10.如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
D.5
二、填空题(每题3分,共30分)
11.已知 则 的值为 .
12.如图,若△ABC∽△DEF,相似比为3:2,已知AB=4,BC=3,则EF= .
13.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD 的高度应为 cm.
14.如图,已知△ABC与是以坐标原点O为位似中心的位似图形,且 若点A(-1,0),点 则
15.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
16.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .
17.如图所示,在正方形ABCD中,G为CD边的中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F.已知FG=2,则线段AE的长度为 .
18.已知三个边长分别为2cm,3cm,5cm的正方形如图排列,则图中阴影部分的面积为 .
19.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,则DE= .
20.如图,在直角三角形ABC中(∠C=90°)放置边长分别为3,4,x的三个正方形,则x的值为 .
三、解答题(共60分)
21.(10分)如图,在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM,并说明理由.(不写作法,保留作图痕迹)
22.(12分)在如图所示的平面直角坐标系中,已知点A(-3,-3),点B(-1,-3),点C(-1,-1).
(1)画出△ABC.
(2)画出△ABC关于x轴对称的△A B C ,并写出A 点的坐标: .
(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到 △A B C ,画出△A B C ,并写出A 点的坐标: .
23.(12分)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.
(2)若AB=13,BC=10,求线段DE的长.
24.(12分)如图,矩形ABCD中,点E是AB的中点,过点E 作CE的垂线,交CD的延长线于点G,交AD于点F,且点F是AD的中点.
(1)求证:△EBC∽△CEG.
(2)求证:
25.(14分)已知:△ABC中,∠BAC=90°,AB=AC,D为BC 的中点,F,E是AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
(1)如图①,求证:∠FDC=∠AEB.
(2)如图①,若AE=3CE=6,求BG的长.
(3)如图②,若F为AC上任意一点,连接AG.
求证:∠EAG=∠ABE.
参考答案
1.A 2.B 3.A 4.C 5.C 6.B 7.D 8.D
9.B [解析]∵AB⊥AD,AD⊥DE,∴∠BAD=∠ADE=90°,∴DE∥AB,∴∠CED=∠CAB.
∵∠C=∠C,∴△CED∽△CAB.
∵DE=1,AB=2,即DE:AB=
10.C [解析]设AD=2x,则BD=x,AB=3x.
∵DE∥BC,
∴∠ADE=∠ACD.∵∠A=∠A,∴△ADE∽△ACD,
设
12.2 13.16 15.4.5 17.12
18.3.75cm [解析]根据相似的性质可知 解得x=2.5,
∴阴影梯形的上底是3-2.5=0.5(cm).
再根据相似的性质可知 解得y=1,∴梯形的下底是3-1=2(cm),
∴阴影梯形的面积是(0.5+2)×3÷2=3.75( cm ).
[解析]∵∠ACB=90°,AB=10,BC=6,∴AC=8.
∵BD平分∠ABC,∴∠ABE=∠CBE.∵CD∥AB,∴∠D=∠ABE,∴∠D=∠CBE,∴CD=BC=6,
∴CE
20.7
21.解:如图所示,点P即为所求.
理由:∵DP⊥AM,∴∠APD=∠ABM=90°.
∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA ∽△ABM.
22.解:(1)图略. (2)图略.(-3,3) (3)图略.(6,6)
23.(1)证明:∵AD为BC边上的中线,∴BD=CD.
∵AB=AC,∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,∴△BDE∽△CAD.
(2)解:在Rt△ADB中,
∴AD=
24.证明:(1)∵CE⊥EG,∴∠GEC=90°.
∵四边形ABCD是矩形,∴∠EBC=90°,AB∥CD,
∴∠BEC=∠ECG.
(2)∵E,F分别是AB,AD的中点,∴EF是△ABD的中位线,
∠DFG,AF=DF,∴△AFE≌△DFG(AAS),∴GF=
∵四边形ABCD是矩形,∴∠ADC=90° ,∴∠ADG=180°- ∠ADC =90°,∴∠GDF=∠GEC.
∵∠G=∠G,∴△GFD∽△GCE,
25.(1)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠C=45°.
∵∠BGD=∠EGF=45° ,∴∠BGD=∠C.
∵∠FDC=∠EBC+∠BGD,∠AEB=∠EBC+∠C,∴∠FDC=∠AEB.
(2)解:∵AE=3CE=6,∴CE=2,AE=6,∴AB=AC=8.
∵∠A=90°,∴BE=
D 是BC的中点,
即
(3)证明:如图,连接AD.∵AB=AC,D为BC的中点,∴AD⊥BC,∴∠ADB=90°=∠BAC.
∴AB =BD · BC.
由(2)知△
∴∠AGB=∠BAE=90°,∴∠EAG+∠BAG=∠BAG+∠ABE=90°,∴∠EAG=∠ABE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
