4.6圆与圆的位置关系 学案

学科数学 年级 初三 学制 六三 设计人时间：13年11月22日
课题：圆与圆的位置关系 课型：新授课学习目标1、通过作图并用运动的观点，经历两圆的五种位置关系的产生过程；2、采用合作交流的方法，体验两圆内切与外切的区别，两圆内含与外离的区别；3、从两圆的交点个数及两圆的半径、圆心距之间的数量关系两方面理解两圆的五种位置关系；4、利用两圆的位置关系解决有关实际问题。二重点、难点、考点两圆的五种位置关系与两圆的半径、圆心距之间的数量关系三、自学指导1、创设情景，引入新课出示有关两圆关系的图片，如：奥运会的五环标志（圆与圆相交）自行车的两个车轮（两圆外离），两个齿轮组成的传动装置（两圆外切、内切）、飞镖靶（两圆内含）等。板书课题：圆与圆的位置关系2、探究两圆的位置关系合作学习：（1）画一条线段O1O2，在O1O2上取一点T，分别以点O1，O2为圆心，O1T，O2T为半径作⊙O1和⊙O2，⊙O1和⊙O2有几个公共点？两圆的圆心距O1O2与两圆的半径之间有怎样的数量关系？（2）如果把点T取在线段O1O2的延长线上，再画⊙O1和⊙O2，此时两圆有几个公共点？两圆的圆心距离O1O2两圆的半径之间有怎样的数量关系？ 归纳：当两圆有唯一的公共点时，叫做 ，唯一的公共点叫做切点。（如图1）相切的两个圆除了切点外，一个圆上的点都在另一个圆的外部时，我们就说这两个圆；，（如图2）相切的两个圆，除了切点外，一个圆上的点都在另一个圆的内部时，我们就说这两个圆。
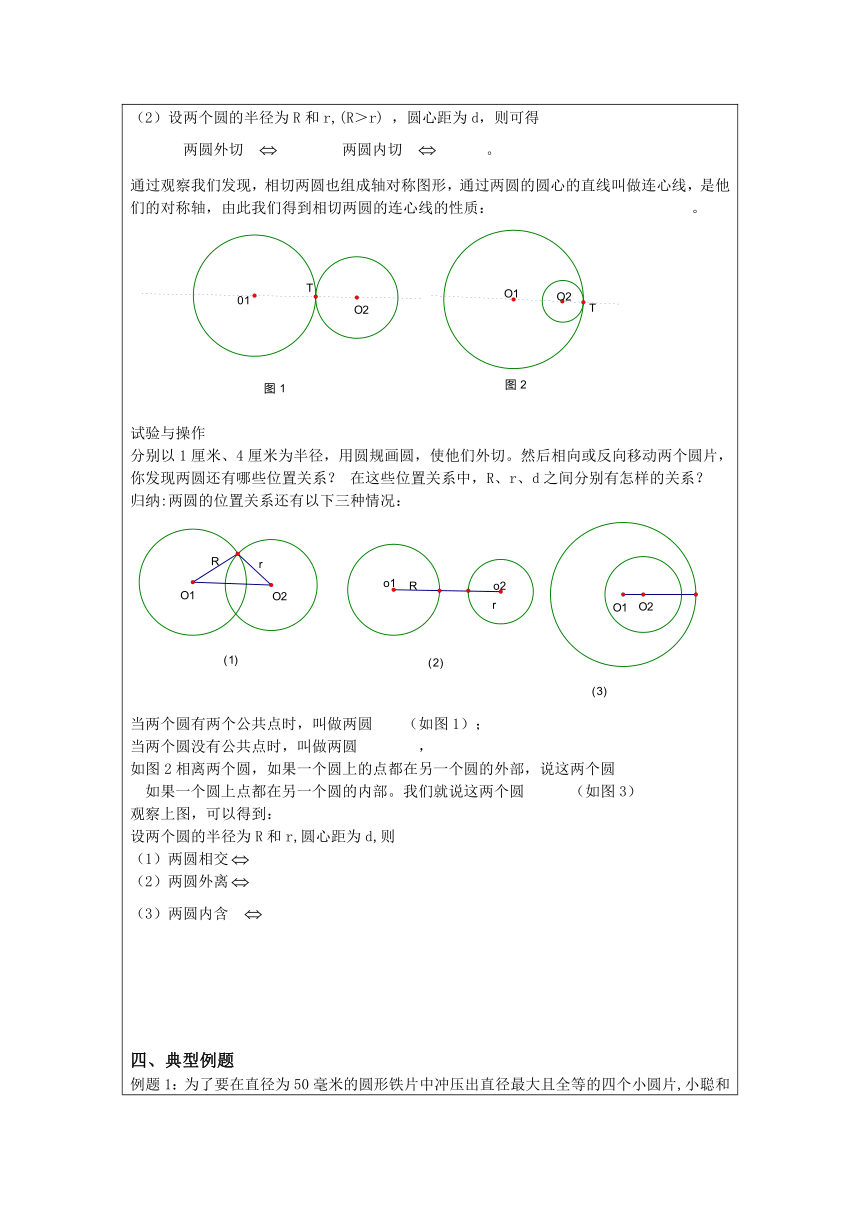
（2）设两个圆的半径为R和r,(R＞r) ，圆心距为d，则可得两圆外切 两圆内切 。通过观察我们发现，相切两圆也组成轴对称图形，通过两圆的圆心的直线叫做连心线，是他们的对称轴，由此我们得到相切两圆的连心线的性质： 。试验与操作分别以1厘米、4厘米为半径，用圆规画圆，使他们外切。然后相向或反向移动两个圆片，你发现两圆还有哪些位置关系？ 在这些位置关系中，R、r、d之间分别有怎样的关系？ 归纳:两圆的位置关系还有以下三种情况：当两个圆有两个公共点时，叫做两圆 （如图1）；当两个圆没有公共点时，叫做两圆 ，如图2相离两个圆，如果一个圆上的点都在另一个圆的外部，说这两个圆 如果一个圆上点都在另一个圆的内部。我们就说这两个圆 （如图3）观察上图，可以得到：设两个圆的半径为R和r,圆心距为d,则（1）两圆相交（2）两圆外离（3）两圆内含 四、典型例题例题1：为了要在直径为50毫米的圆形铁片中冲压出直径最大且全等的四个小圆片,小聪和他的同学设计了如图的方案,其中每相邻两个小圆外切,每个小圆与⊙O内切.这是一个具有4条对称轴AC,BD,L1L2的对称图形.试求出小圆片的直径(结果保留3个有效数字)（2）已知⊙A、 ⊙B相切，圆心距为10cm，其中⊙A的半径为4cm，求⊙B的半径．（注意相切分外切和内切两种）四、对应训练1. 已知两圆的圆心距是3，两圆的半径分别1,3，则这两个圆的位置关系是（ ) A．外离 B．外切 C．相交 D．内切2. ⊙O的半径是1.5，直线与⊙0相交，圆心O到直线的距离是d，则d应满足 ( ) A. d>3 B. 1.5