人教A版必修2高中数学1.3.2球的体积和表面积 基础训练(含解析)
文档属性
| 名称 | 人教A版必修2高中数学1.3.2球的体积和表面积 基础训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览




文档简介
球的体积和表面积
基础练
题组一 球的体积和表面积
1.一平面截一球得到直径是6 cm的圆面,球心到这个圆面的距离是4 cm,则该球的体积是 ( )
A. cm3 B. cm3
C. cm3 D. cm3
2.已知球的体积是,则此球的表面积是 ( )
A.12π B.16π C. D.
3.若三个球的表面积之比为1∶4∶9,则这三个球的体积之比为 .
题组二 与三视图有关的球的体积和表面积
4.某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B.
C. D.
5.一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为 .
题组三 与球的截面有关的球的体积和表面积
6.已知长方体ABCD-A1B1C1D1的各个顶点都在球面上,AB=AD=8,AA1=6,过棱AB作该球的截面,则当截面面积最小时,球心到截面的距离为 ( )
A.3 B.4 C.5 D.6
7.如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为 ( )
A. cm3 B. cm3
C. cm3 D. cm3
8.球O的一个截面圆的圆心为M,圆M的半径为,OM的长度为球O的半径的一半,则球O的表面积为 ( )
A.4π B. C.12π D.16π
题组四 球的切、接问题
9.在正方体ABCD-A1B1C1D1中,三棱锥A1-BC1D的内切球的表面积为16π,则正方体外接球的体积为 ( )
A.288π B.36π C.72π D.81π
10.已知四面体A-BCD满足:AB=BC=CD=DA=AC=1,BD=,则四面体A-BCD外接球的表面积为 .
11.已知四面体的各面都是棱长为a的正三角形,求它外接球的体积及内切球的半径.
提升练
一、选择题
1.已知各顶点都在一个球面上的正四棱锥的高为3,体积为6,则这个球的表面积为 ( )
A.16π B.20π C.24π D.32π
2.等体积的球和正方体的表面积S球与S正方体的大小关系是 ( )
A.S正方体>S球 B.S正方体C.S正方体=S球 D.无法确定
3.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,某园林建筑为四角攒尖,它的主要部分的轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面面积的3倍,则此正四棱锥的内切球半径与底面边长之比为 ( )
A. B.
C. D.
4.已知三棱锥A-BCD中,AB=CD=,AD=BC=2,AC=BD=,则三棱锥A-BCD的外接球的体积是 ( )
A.2π B.π C.6π D.3π
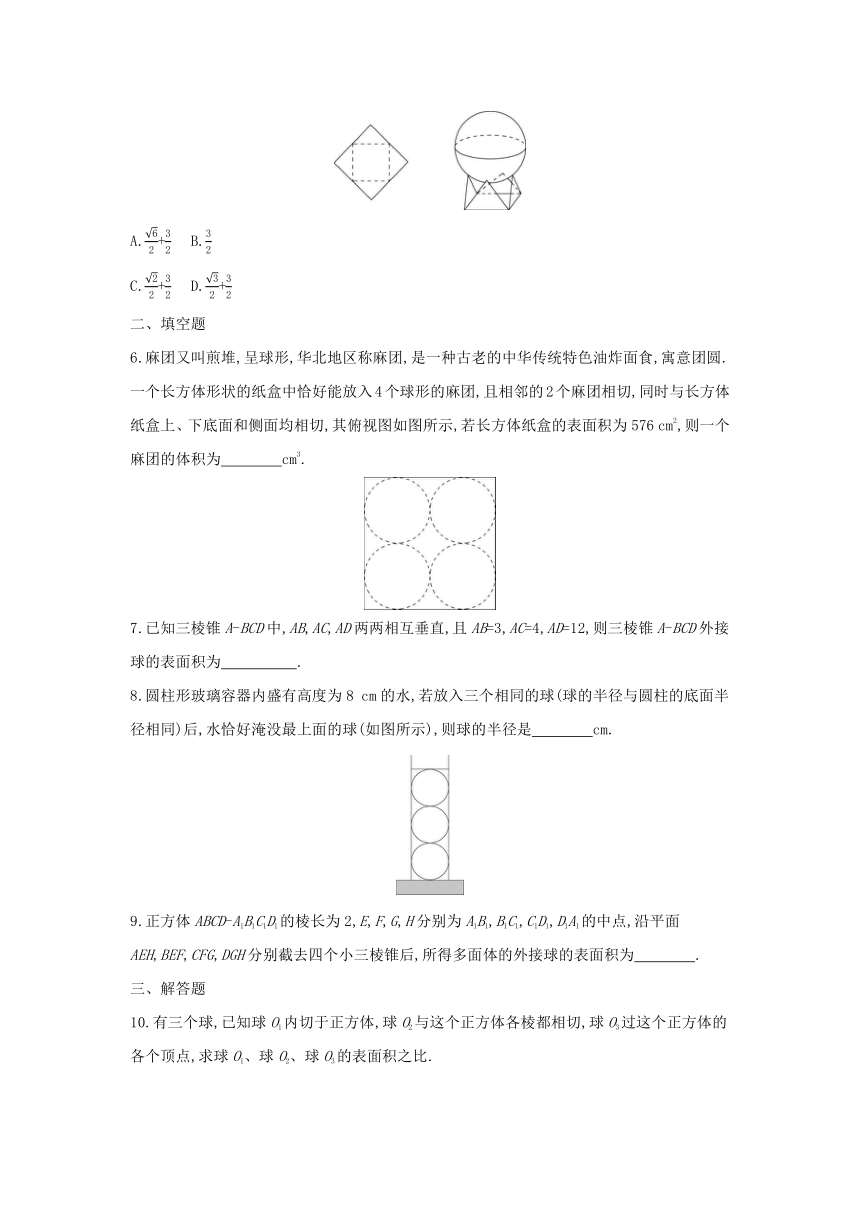
5.如图,用一边长为的正方形硬纸,按各边中点垂直折起4个小三角形,做成一个蛋巢,将体积为的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
A.+ B.
C.+ D.+
二、填空题
6.麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆.一个长方体形状的纸盒中恰好能放入4个球形的麻团,且相邻的2个麻团相切,同时与长方体纸盒上、下底面和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为576 cm2,则一个麻团的体积为 cm3.
7.已知三棱锥A-BCD中,AB,AC,AD两两相互垂直,且AB=3,AC=4,AD=12,则三棱锥A-BCD外接球的表面积为 .
8.圆柱形玻璃容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.
9.正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别为A1B1,B1C1,C1D1,D1A1的中点,沿平面AEH,BEF,CFG,DGH分别截去四个小三棱锥后,所得多面体的外接球的表面积为 .
三、解答题
10.有三个球,已知球O1内切于正方体,球O2与这个正方体各棱都相切,球O3过这个正方体的各个顶点,求球O1、球O2、球O3的表面积之比.
参考答案:
基础练
1.C 2.B 4.A 6.C 7.A
8.D 9.A
1.C 根据球的截面性质,得球的半径R==5(cm),
所以V球=πR3= cm3.故选C.
2.B 设球的半径为R,则由已知得πR3=,解得R=2,故S球=4πR2=16π.
3.答案 1∶8∶27
解析 设三个球的半径分别为R1,R2,R3,∵三个球的表面积之比为1∶4∶9,
∴4π∶4π∶4π=1∶4∶9,
∴∶∶=1∶4∶9,
∴R1∶R2∶R3=1∶2∶3,
∴∶∶=1∶8∶27,
∴V1∶V2∶V3=π∶π∶π=∶∶=1∶8∶27.
4.A 结合三视图可知该几何体是一个组合体,下半部分是一个底面边长为2,高为的正四棱锥,上半部分是一个半径为1的半球,
所以该几何体的体积V=π×13+×22×=,故选A.
5.答案 16π
解析 该几何体是从一个球中挖去个球后剩余的部分,所以该几何体的表面积为×(4π×22)+2×=16π.
6.C 过棱AB作该球的截面,当截面面积最小时,截面的直径为AB=8,
∵长方体ABCD-A1B1C1D1的各个顶点都在球面上,AB=AD=8,AA1=6,
∴球的半径为×=,
∴球心到截面的距离为=5.
故选C.
7.A 设球的半径为R cm,则由题意知球被正方体上底面截得的圆面的半径为4 cm,球心到截面圆的距离为(R-2)cm,
则R2=(R-2)2+42,解得R=5.
∴球的体积为= cm3.
8.D 如图所示,由题意知AM=.
设球O的半径为R,则OM=R,OA=R.
在Rt△OMA中,有OM2+AM2=OA2,即R2+3=R2,解得R=2,所以球O的表面积为4π×22=16π.
9.A 设正方体的棱长为a,则BD=a,
∵三棱锥A1-BC1D的内切球的表面积为16π,∴三棱锥A1-BC1D的内切球半径为2,设三棱锥A1-BC1D的内切球的球心为O,A1到平面BC1D的距离为h,则=4,
即×h=4××2,解得h=8,
∴h=×a=8,∴a=4.
∴正方体外接球的半径R=×a=6,
∴正方体外接球的体积为πR3=288π,
故选A.
10.答案 2π
关键点拨 求解球的内切与外接问题的关键是根据条件确定好球心,由题意可知△ABD,△CBD均为直角三角形,则四面体外接球的球心为BD的中点,进而可求得其半径.
解析 四面体A-BCD如图所示,
因为在四面体A-BCD中,AB=BC=CD=DA=AC=1,BD=,
所以AB2+AD2=BD2,BC2+CD2=BD2,则△ABD,△CBD均为直角三角形,
故该四面体外接球的球心为BD的中点,
即半径R=BD=,
故表面积S=4πR2=2π.
11.解析 如图,设SO1是四面体S-ABC的高,则外接球的球心O在SO1上.
设外接球的半径为R.
∵四面体的棱长均为a,O1为正三角形ABC的中心,
∴AO1=×a=a,
SO1===a,
在Rt△OO1A中,R2=A+O=A+(SO1-R)2,
即R2=a2+a-R2,
解得R=a,
∴所求外接球的体积V=πR3=πa3.
易知OO1为内切球的半径,OO1=a-a=a,
∴所求内切球的半径为a.
提升练
1.A 2.A 3.B 4.B 5.D
一、选择题
1.A 设正四棱锥的高为h,底面边长为a,则h=3,由V=a2h=6,得a=,则底面正方形的对角线长为2,由题意知,球心在正四棱锥的高上,设球的半径为r,则(3-r)2+()2=r2,解得r=2,故S球=4πr2=16π.故选A.
2.A 设正方体的棱长为a,球的半径为R.
由题意得V=πR3=a3,所以a=,R=.所以S正方体=6a2=6=,S球=4πR2=,所以S正方体>S球.
3.B 正四棱锥P-ABCD如图所示,设AB=a,正四棱锥的高PH=h,则斜高为,由题意得4××a×=3a2,所以h=a.则S表=a2+4×a=4a2.
设正四棱锥的内切球半径为r,由等积法可得×a2×h=×4a2×r,所以r==a,所以=,故选B.
4.B 将三棱锥A-BCD放置于长方体中,如图所示,
则长方体的外接球就是三棱锥A-BCD的外接球.
设过长方体一个顶点的三条棱长分别为a,b,c,
∵AB=CD=,AD=BC=2,AC=BD=,
∴长方体的体对角线长为
=
==,
可得外接球的半径R=,
因此三棱锥A-BCD的外接球的体积V=×π×3=π.
故选B.
5.D 由题意,可得蛋巢的底面是边长为1的正方形,则经过4个小三角形的顶点截鸡蛋(球)所得的截面圆的直径为1.因为鸡蛋的体积为 ,所以鸡蛋的半径为1,所以球心到截面圆的距离为=,因为垂直折起的4个小直角三角形的高为,所以鸡蛋最高点与蛋巢底面的距离为1++=+.故选D.
二、填空题
6.答案 36π
解析 设麻团的半径为r cm,则根据题意易得长方体纸盒的长为4r cm,宽为4r cm,高为2r cm,则2(4r×4r+4r×2r+4r×2r)=576,解得r=3(负值舍去),所以一个麻团的体积为πr3=36π cm3.
7.答案 169π
解析 因为AB,AC,AD两两相互垂直,所以可将三棱锥A-BCD补形为以AD,AB,AC分别为长、宽、高的长方体,则该长方体的外接球即为三棱锥A-BCD的外接球,所以该球的半径R==,故其表面积S=4πR2=169π.
8.答案 4
解析 设球的半径为r cm,则由题意可得3V球+V水=V,即3×πr3+πr2×8=πr2×6r,所以r=4.故球的半径是4 cm.
9.答案
解析 如图,设多面体的外接球的球心为O,平面EFGH截球所得的截面圆圆心为O1,平面ABCD截球所得的截面圆圆心为O2,连接OO1,OO2,OF,OC,O1F,O2C,设球O的半径为R,OO1=m,则OO2=2-m,分别在Rt△OO1F和Rt△OO2C中,有R2-m2=1,R2-(2-m)2=2,两式相减得4m-4=1,解得m=,所以R2=,故S球=4πR2=.
三、解答题
10.解析 设正方体的棱长为a.
球O1为正方体的内切球,球心O1是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,如图①所示,设球O1的半径为r1,表面积为S1,则2r1=a,解得r1=,所以S1=4π=πa2.
球O2与正方体各棱的切点为各棱的中点,过正方体的两个相对面的面对角线作截面,如图②所示,设球O2的半径为r2,表面积为S2,则2r2=a,解得r2=a,所以S2=4π=2πa2.
球O3过正方体的各个顶点,即正方体的各个顶点都在球面上,过正方体的体对角线作截面,如图③所示,设球O3的半径为r3,表面积为S3,则2r3=a,解得r3=a,所以S3=4π=3πa2.
故球O1、球O2、球O3的表面积之比S1∶S2∶S3=πa2∶2πa2∶3πa2=1∶2∶3.
基础练
题组一 球的体积和表面积
1.一平面截一球得到直径是6 cm的圆面,球心到这个圆面的距离是4 cm,则该球的体积是 ( )
A. cm3 B. cm3
C. cm3 D. cm3
2.已知球的体积是,则此球的表面积是 ( )
A.12π B.16π C. D.
3.若三个球的表面积之比为1∶4∶9,则这三个球的体积之比为 .
题组二 与三视图有关的球的体积和表面积
4.某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B.
C. D.
5.一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为 .
题组三 与球的截面有关的球的体积和表面积
6.已知长方体ABCD-A1B1C1D1的各个顶点都在球面上,AB=AD=8,AA1=6,过棱AB作该球的截面,则当截面面积最小时,球心到截面的距离为 ( )
A.3 B.4 C.5 D.6
7.如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为 ( )
A. cm3 B. cm3
C. cm3 D. cm3
8.球O的一个截面圆的圆心为M,圆M的半径为,OM的长度为球O的半径的一半,则球O的表面积为 ( )
A.4π B. C.12π D.16π
题组四 球的切、接问题
9.在正方体ABCD-A1B1C1D1中,三棱锥A1-BC1D的内切球的表面积为16π,则正方体外接球的体积为 ( )
A.288π B.36π C.72π D.81π
10.已知四面体A-BCD满足:AB=BC=CD=DA=AC=1,BD=,则四面体A-BCD外接球的表面积为 .
11.已知四面体的各面都是棱长为a的正三角形,求它外接球的体积及内切球的半径.
提升练
一、选择题
1.已知各顶点都在一个球面上的正四棱锥的高为3,体积为6,则这个球的表面积为 ( )
A.16π B.20π C.24π D.32π
2.等体积的球和正方体的表面积S球与S正方体的大小关系是 ( )
A.S正方体>S球 B.S正方体
3.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,某园林建筑为四角攒尖,它的主要部分的轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面面积的3倍,则此正四棱锥的内切球半径与底面边长之比为 ( )
A. B.
C. D.
4.已知三棱锥A-BCD中,AB=CD=,AD=BC=2,AC=BD=,则三棱锥A-BCD的外接球的体积是 ( )
A.2π B.π C.6π D.3π
5.如图,用一边长为的正方形硬纸,按各边中点垂直折起4个小三角形,做成一个蛋巢,将体积为的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
A.+ B.
C.+ D.+
二、填空题
6.麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆.一个长方体形状的纸盒中恰好能放入4个球形的麻团,且相邻的2个麻团相切,同时与长方体纸盒上、下底面和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为576 cm2,则一个麻团的体积为 cm3.
7.已知三棱锥A-BCD中,AB,AC,AD两两相互垂直,且AB=3,AC=4,AD=12,则三棱锥A-BCD外接球的表面积为 .
8.圆柱形玻璃容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.
9.正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别为A1B1,B1C1,C1D1,D1A1的中点,沿平面AEH,BEF,CFG,DGH分别截去四个小三棱锥后,所得多面体的外接球的表面积为 .
三、解答题
10.有三个球,已知球O1内切于正方体,球O2与这个正方体各棱都相切,球O3过这个正方体的各个顶点,求球O1、球O2、球O3的表面积之比.
参考答案:
基础练
1.C 2.B 4.A 6.C 7.A
8.D 9.A
1.C 根据球的截面性质,得球的半径R==5(cm),
所以V球=πR3= cm3.故选C.
2.B 设球的半径为R,则由已知得πR3=,解得R=2,故S球=4πR2=16π.
3.答案 1∶8∶27
解析 设三个球的半径分别为R1,R2,R3,∵三个球的表面积之比为1∶4∶9,
∴4π∶4π∶4π=1∶4∶9,
∴∶∶=1∶4∶9,
∴R1∶R2∶R3=1∶2∶3,
∴∶∶=1∶8∶27,
∴V1∶V2∶V3=π∶π∶π=∶∶=1∶8∶27.
4.A 结合三视图可知该几何体是一个组合体,下半部分是一个底面边长为2,高为的正四棱锥,上半部分是一个半径为1的半球,
所以该几何体的体积V=π×13+×22×=,故选A.
5.答案 16π
解析 该几何体是从一个球中挖去个球后剩余的部分,所以该几何体的表面积为×(4π×22)+2×=16π.
6.C 过棱AB作该球的截面,当截面面积最小时,截面的直径为AB=8,
∵长方体ABCD-A1B1C1D1的各个顶点都在球面上,AB=AD=8,AA1=6,
∴球的半径为×=,
∴球心到截面的距离为=5.
故选C.
7.A 设球的半径为R cm,则由题意知球被正方体上底面截得的圆面的半径为4 cm,球心到截面圆的距离为(R-2)cm,
则R2=(R-2)2+42,解得R=5.
∴球的体积为= cm3.
8.D 如图所示,由题意知AM=.
设球O的半径为R,则OM=R,OA=R.
在Rt△OMA中,有OM2+AM2=OA2,即R2+3=R2,解得R=2,所以球O的表面积为4π×22=16π.
9.A 设正方体的棱长为a,则BD=a,
∵三棱锥A1-BC1D的内切球的表面积为16π,∴三棱锥A1-BC1D的内切球半径为2,设三棱锥A1-BC1D的内切球的球心为O,A1到平面BC1D的距离为h,则=4,
即×h=4××2,解得h=8,
∴h=×a=8,∴a=4.
∴正方体外接球的半径R=×a=6,
∴正方体外接球的体积为πR3=288π,
故选A.
10.答案 2π
关键点拨 求解球的内切与外接问题的关键是根据条件确定好球心,由题意可知△ABD,△CBD均为直角三角形,则四面体外接球的球心为BD的中点,进而可求得其半径.
解析 四面体A-BCD如图所示,
因为在四面体A-BCD中,AB=BC=CD=DA=AC=1,BD=,
所以AB2+AD2=BD2,BC2+CD2=BD2,则△ABD,△CBD均为直角三角形,
故该四面体外接球的球心为BD的中点,
即半径R=BD=,
故表面积S=4πR2=2π.
11.解析 如图,设SO1是四面体S-ABC的高,则外接球的球心O在SO1上.
设外接球的半径为R.
∵四面体的棱长均为a,O1为正三角形ABC的中心,
∴AO1=×a=a,
SO1===a,
在Rt△OO1A中,R2=A+O=A+(SO1-R)2,
即R2=a2+a-R2,
解得R=a,
∴所求外接球的体积V=πR3=πa3.
易知OO1为内切球的半径,OO1=a-a=a,
∴所求内切球的半径为a.
提升练
1.A 2.A 3.B 4.B 5.D
一、选择题
1.A 设正四棱锥的高为h,底面边长为a,则h=3,由V=a2h=6,得a=,则底面正方形的对角线长为2,由题意知,球心在正四棱锥的高上,设球的半径为r,则(3-r)2+()2=r2,解得r=2,故S球=4πr2=16π.故选A.
2.A 设正方体的棱长为a,球的半径为R.
由题意得V=πR3=a3,所以a=,R=.所以S正方体=6a2=6=,S球=4πR2=,所以S正方体>S球.
3.B 正四棱锥P-ABCD如图所示,设AB=a,正四棱锥的高PH=h,则斜高为,由题意得4××a×=3a2,所以h=a.则S表=a2+4×a=4a2.
设正四棱锥的内切球半径为r,由等积法可得×a2×h=×4a2×r,所以r==a,所以=,故选B.
4.B 将三棱锥A-BCD放置于长方体中,如图所示,
则长方体的外接球就是三棱锥A-BCD的外接球.
设过长方体一个顶点的三条棱长分别为a,b,c,
∵AB=CD=,AD=BC=2,AC=BD=,
∴长方体的体对角线长为
=
==,
可得外接球的半径R=,
因此三棱锥A-BCD的外接球的体积V=×π×3=π.
故选B.
5.D 由题意,可得蛋巢的底面是边长为1的正方形,则经过4个小三角形的顶点截鸡蛋(球)所得的截面圆的直径为1.因为鸡蛋的体积为 ,所以鸡蛋的半径为1,所以球心到截面圆的距离为=,因为垂直折起的4个小直角三角形的高为,所以鸡蛋最高点与蛋巢底面的距离为1++=+.故选D.
二、填空题
6.答案 36π
解析 设麻团的半径为r cm,则根据题意易得长方体纸盒的长为4r cm,宽为4r cm,高为2r cm,则2(4r×4r+4r×2r+4r×2r)=576,解得r=3(负值舍去),所以一个麻团的体积为πr3=36π cm3.
7.答案 169π
解析 因为AB,AC,AD两两相互垂直,所以可将三棱锥A-BCD补形为以AD,AB,AC分别为长、宽、高的长方体,则该长方体的外接球即为三棱锥A-BCD的外接球,所以该球的半径R==,故其表面积S=4πR2=169π.
8.答案 4
解析 设球的半径为r cm,则由题意可得3V球+V水=V,即3×πr3+πr2×8=πr2×6r,所以r=4.故球的半径是4 cm.
9.答案
解析 如图,设多面体的外接球的球心为O,平面EFGH截球所得的截面圆圆心为O1,平面ABCD截球所得的截面圆圆心为O2,连接OO1,OO2,OF,OC,O1F,O2C,设球O的半径为R,OO1=m,则OO2=2-m,分别在Rt△OO1F和Rt△OO2C中,有R2-m2=1,R2-(2-m)2=2,两式相减得4m-4=1,解得m=,所以R2=,故S球=4πR2=.
三、解答题
10.解析 设正方体的棱长为a.
球O1为正方体的内切球,球心O1是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,如图①所示,设球O1的半径为r1,表面积为S1,则2r1=a,解得r1=,所以S1=4π=πa2.
球O2与正方体各棱的切点为各棱的中点,过正方体的两个相对面的面对角线作截面,如图②所示,设球O2的半径为r2,表面积为S2,则2r2=a,解得r2=a,所以S2=4π=2πa2.
球O3过正方体的各个顶点,即正方体的各个顶点都在球面上,过正方体的体对角线作截面,如图③所示,设球O3的半径为r3,表面积为S3,则2r3=a,解得r3=a,所以S3=4π=3πa2.
故球O1、球O2、球O3的表面积之比S1∶S2∶S3=πa2∶2πa2∶3πa2=1∶2∶3.
