人教版七年级数学下册 5.1.2 垂线(第2课时)教案
文档属性
| 名称 | 人教版七年级数学下册 5.1.2 垂线(第2课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 835.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:13:06 | ||
图片预览

文档简介
5.1.2 垂线
第2课时
一、教学目标
【知识与技能】
1. 理解垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线段 .
2. 掌握点到直线的距离的概念,并会度量点到直线的距离.
3. 掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
【过程与方法】
学生经历画、观察、量、思考、归纳、应用等一系列的过程,初步了解解决实际问题的方法,培养学生动手实践能力和解决实际问题的意识。
【情感态度与价值观】
在探索与运用“垂线段最短”这一性质的过程中感受学习数学图形的乐趣。
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
探究垂线段最短的过程
【教学难点】
理解垂线段最短
五、课前准备
教师:课件、三角尺、直尺、量角器等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
(二)探索新知
1.出示课件4-5,探究点到直线的距离
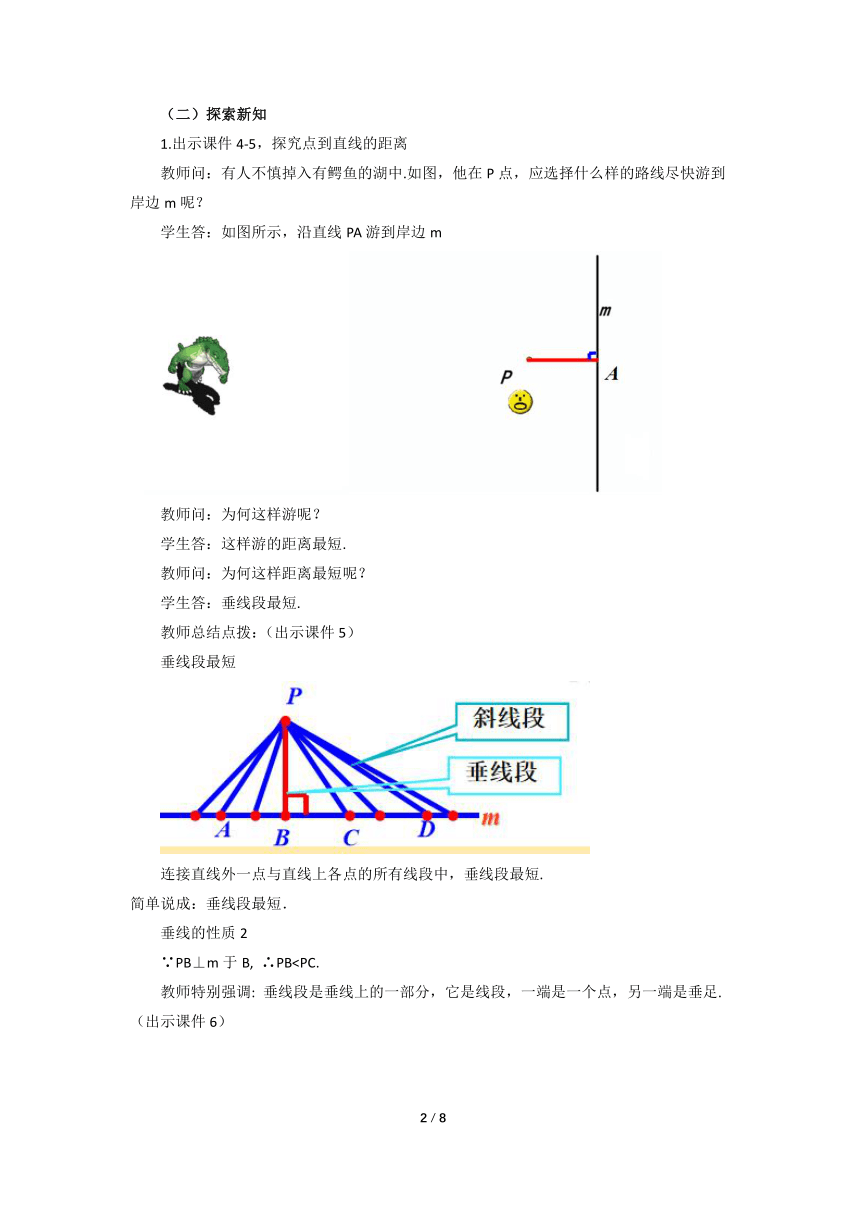
教师问:有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
学生答:如图所示,沿直线PA游到岸边m
教师问:为何这样游呢?
学生答:这样游的距离最短.
教师问:为何这样距离最短呢?
学生答:垂线段最短.
教师总结点拨:(出示课件5)
垂线段最短
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
垂线的性质2
∵PB⊥m于B, ∴PB教师特别强调: 垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.(出示课件6)
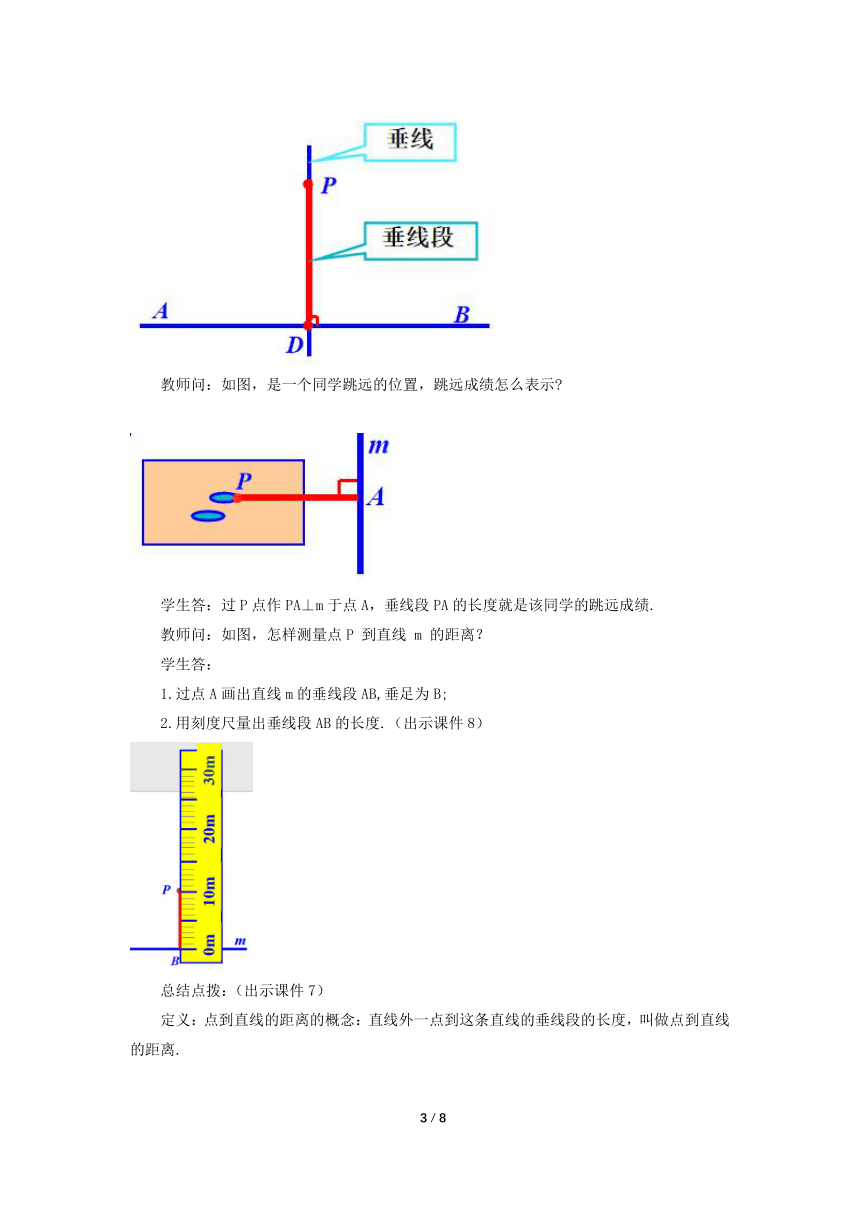
教师问:如图,是一个同学跳远的位置,跳远成绩怎么表示
学生答:过P点作PA⊥m于点A,垂线段PA的长度就是该同学的跳远成绩.
教师问:如图,怎样测量点P 到直线 m 的距离?
学生答:
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.(出示课件8)
总结点拨:(出示课件7)
定义:点到直线的距离的概念:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
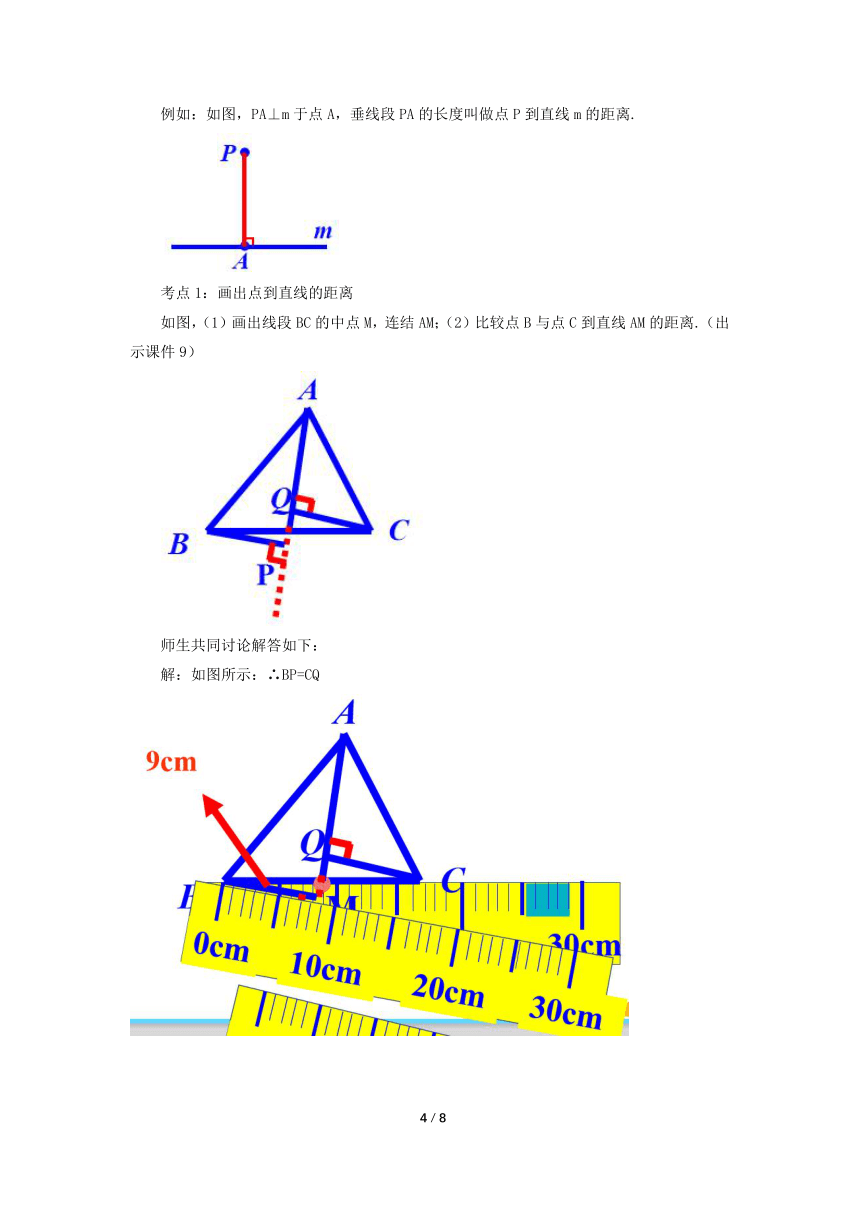
例如:如图,PA⊥m于点A,垂线段PA的长度叫做点P到直线m的距离.
考点1:画出点到直线的距离
如图,(1)画出线段BC的中点M,连结AM;(2)比较点B与点C到直线AM的距离.(出示课件9)
师生共同讨论解答如下:
解:如图所示:∴BP=CQ
出示课件10,学生自主练习后口答,教师订正.
考点2:测量点线间距离
如图,量出
(1)村庄A与货场B的距离, (2)货场B到铁道的距离.(出示课件11)
学生独立思考后,师生共同解答.
解:如图所示:
出示课件12,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件13-19)
练习课件第13-19页题目,约用时20分钟.
(四)课堂小结(出示课件20)
(五)课前预习
预习下节课(28.1第2课时)的相关内容.
知道余弦、正切、锐角三角函数的定义
七、课后作业
教材第64页练习第1,2题.
八、板书设计:
第2课时
1.垂直的概念:如果两条直线相交所成的四个角中,有一个是直角,就说这两条直线互相垂直.
2.垂线的性质1:同一平面内,经过一点有且只有一条直线与已知直线垂直.
3.垂线的性质2:直线外一点与直线上各点连结的所有线段中.垂线段最短.
4.考点讲解
考点1 考点2
九、教学反思:
成功之处:教学中利用学生已有知识与心理特点,本节课以生活中的实际问题出发,激发学生的好奇心,通过学生自己画、观察、量、思考、归纳等一系列的过程。设计层层递进,在探究性质的过程中,学生经历动手画---用眼直观观察----测量线段、角----归纳规律---用几何画板验证,让他们能更好的理解“垂线段最短”这一事实。拉长了学生探究学习的过程,培养了学生“几何直观”意识。
本节课借助现代信息技术,让学生直观感受信息技术在数学中的应用。拍摄视频还原生活情境;几何画板的测量和动画功能给予学生以直观感受;seewo授课助手的应用加强了课堂的互动性和即时性。
不足之处:本节课中有的问题提得还有些生硬,教学还需更自然。
9 / 9
第2课时
一、教学目标
【知识与技能】
1. 理解垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线段 .
2. 掌握点到直线的距离的概念,并会度量点到直线的距离.
3. 掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
【过程与方法】
学生经历画、观察、量、思考、归纳、应用等一系列的过程,初步了解解决实际问题的方法,培养学生动手实践能力和解决实际问题的意识。
【情感态度与价值观】
在探索与运用“垂线段最短”这一性质的过程中感受学习数学图形的乐趣。
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
探究垂线段最短的过程
【教学难点】
理解垂线段最短
五、课前准备
教师:课件、三角尺、直尺、量角器等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
(二)探索新知
1.出示课件4-5,探究点到直线的距离
教师问:有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
学生答:如图所示,沿直线PA游到岸边m
教师问:为何这样游呢?
学生答:这样游的距离最短.
教师问:为何这样距离最短呢?
学生答:垂线段最短.
教师总结点拨:(出示课件5)
垂线段最短
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
垂线的性质2
∵PB⊥m于B, ∴PB
教师问:如图,是一个同学跳远的位置,跳远成绩怎么表示
学生答:过P点作PA⊥m于点A,垂线段PA的长度就是该同学的跳远成绩.
教师问:如图,怎样测量点P 到直线 m 的距离?
学生答:
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.(出示课件8)
总结点拨:(出示课件7)
定义:点到直线的距离的概念:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
例如:如图,PA⊥m于点A,垂线段PA的长度叫做点P到直线m的距离.
考点1:画出点到直线的距离
如图,(1)画出线段BC的中点M,连结AM;(2)比较点B与点C到直线AM的距离.(出示课件9)
师生共同讨论解答如下:
解:如图所示:∴BP=CQ
出示课件10,学生自主练习后口答,教师订正.
考点2:测量点线间距离
如图,量出
(1)村庄A与货场B的距离, (2)货场B到铁道的距离.(出示课件11)
学生独立思考后,师生共同解答.
解:如图所示:
出示课件12,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件13-19)
练习课件第13-19页题目,约用时20分钟.
(四)课堂小结(出示课件20)
(五)课前预习
预习下节课(28.1第2课时)的相关内容.
知道余弦、正切、锐角三角函数的定义
七、课后作业
教材第64页练习第1,2题.
八、板书设计:
第2课时
1.垂直的概念:如果两条直线相交所成的四个角中,有一个是直角,就说这两条直线互相垂直.
2.垂线的性质1:同一平面内,经过一点有且只有一条直线与已知直线垂直.
3.垂线的性质2:直线外一点与直线上各点连结的所有线段中.垂线段最短.
4.考点讲解
考点1 考点2
九、教学反思:
成功之处:教学中利用学生已有知识与心理特点,本节课以生活中的实际问题出发,激发学生的好奇心,通过学生自己画、观察、量、思考、归纳等一系列的过程。设计层层递进,在探究性质的过程中,学生经历动手画---用眼直观观察----测量线段、角----归纳规律---用几何画板验证,让他们能更好的理解“垂线段最短”这一事实。拉长了学生探究学习的过程,培养了学生“几何直观”意识。
本节课借助现代信息技术,让学生直观感受信息技术在数学中的应用。拍摄视频还原生活情境;几何画板的测量和动画功能给予学生以直观感受;seewo授课助手的应用加强了课堂的互动性和即时性。
不足之处:本节课中有的问题提得还有些生硬,教学还需更自然。
9 / 9
