人教版七年级数学下册5.3.1 平行线的性质(第1课时)教案
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线的性质(第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 86.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览



文档简介
5.3.1 平行线的性质
第1课时
一、教学目标
【知识与技能】
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
【过程与方法】
经历观察,猜想,操作,交流,归纳,推理等活动,培养学生的概括能力和逻辑思维能力.
【情感态度与价值观】
通过学生动手操作,观察来发展学生的空间观念,培养及主动探索和合作能力.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
平行线的性质,区分平行线的判定方法和性质.
【教学难点】
区分平行线的判定方法和性质.
五、课前准备
教师:课件、三角尺、直尺、量角器等.
学生:三角尺、铅笔、量角器、练习本.
六、教学过程
(一)导入新课(出示课件2)
【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
(二)探索新知
1.出示课件4-7,探究两直线平行,同位角相等
教师问:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
教师依次展示学生答案:
学生1答:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120° °
角 ∠5 ∠6 ∠7 ∠8
度数
学生2答:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120°
角 ∠5 ∠6 ∠7 ∠8
度数
学生3答:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120°
学生4答:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120°
教师总结如下:如下表:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120° 60° 120°
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120° 60° 120°
教师问:∠1~ ∠8中,哪些是同位角?
学生答:同位角有:∠1和∠5,∠4和∠8,∠2和∠6,∠3和∠7.
教师问:同位角的度数之间有什么关系?
学生答:同位角的度数相等.
教师问:由此你得到什么猜想?
学生答:同位角的度数相等.
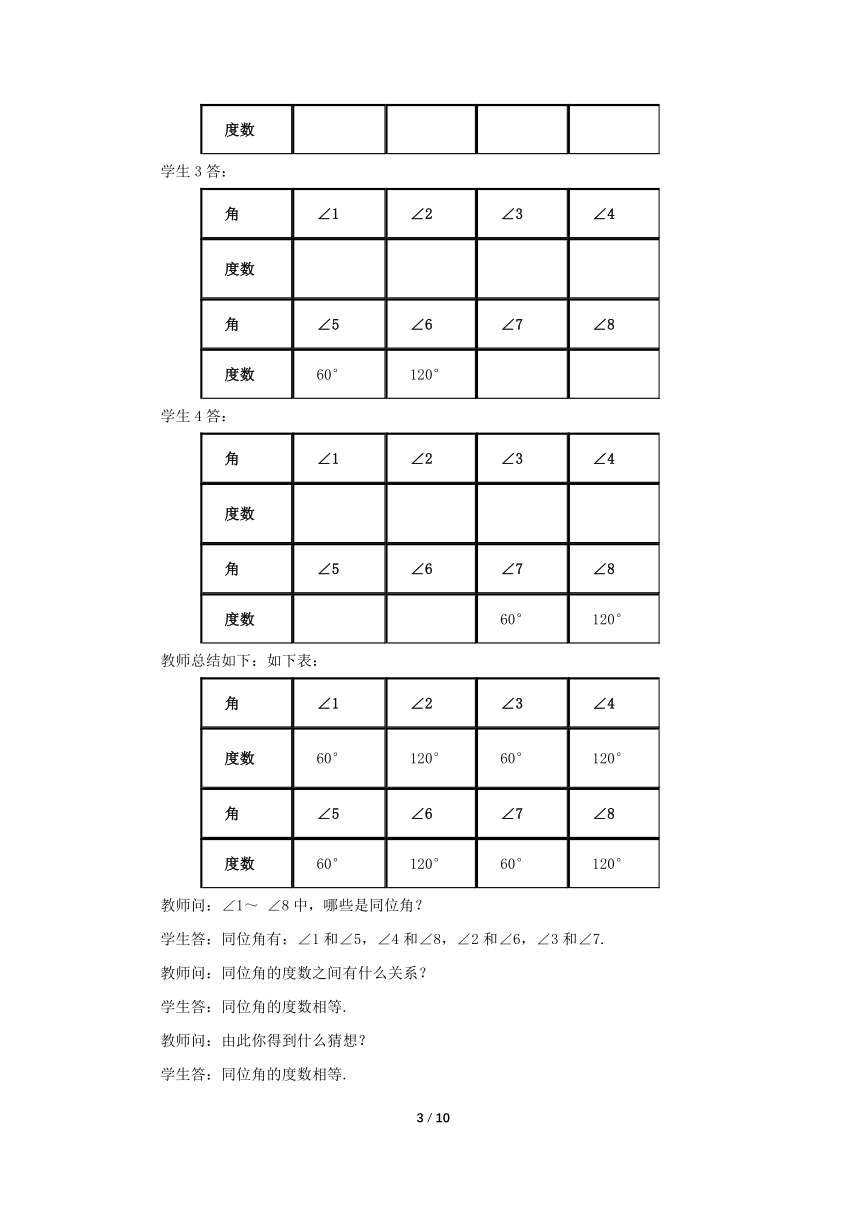
教师问:再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?如下图:
学生测量后答:成立.
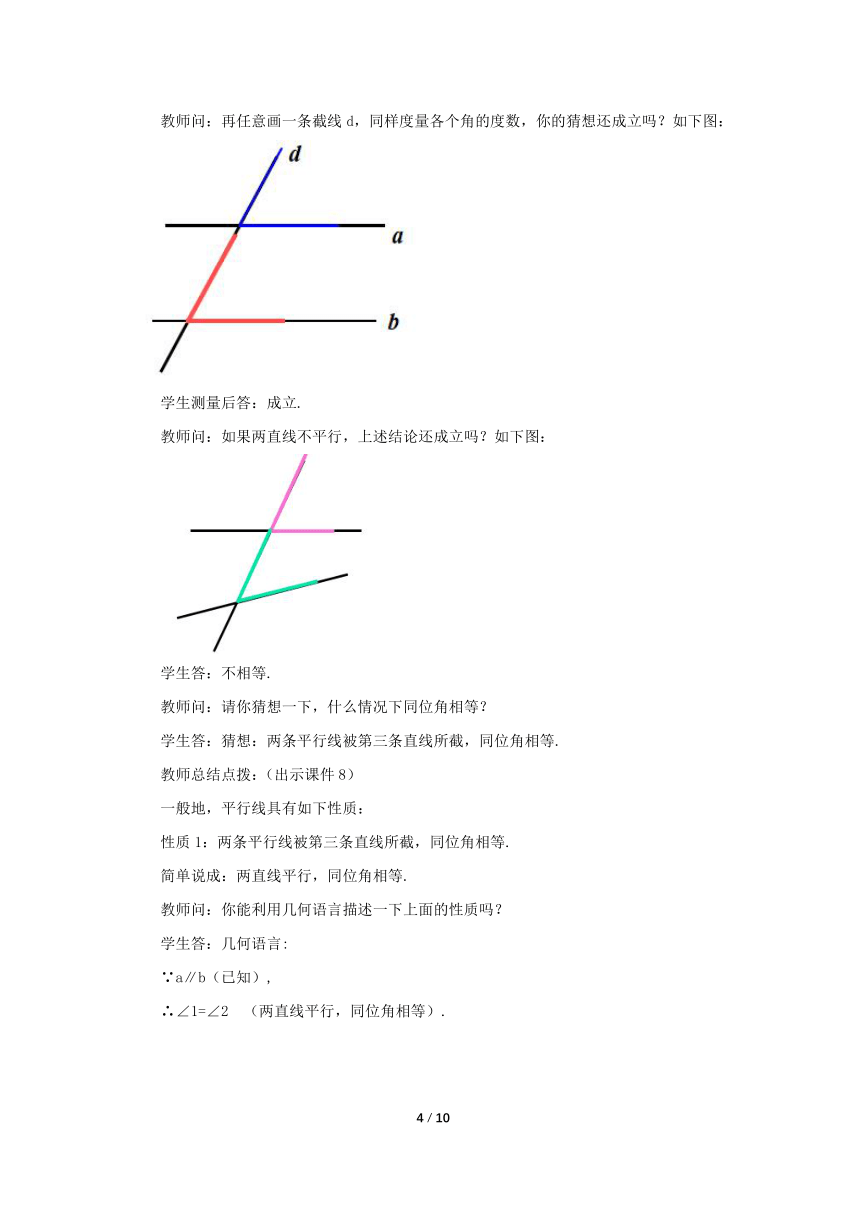
教师问:如果两直线不平行,上述结论还成立吗?如下图:
学生答:不相等.
教师问:请你猜想一下,什么情况下同位角相等?
学生答:猜想:两条平行线被第三条直线所截,同位角相等.
教师总结点拨:(出示课件8)
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
教师问:你能利用几何语言描述一下上面的性质吗?
学生答:几何语言:
∵a∥b(已知),
∴∠1=∠2 (两直线平行,同位角相等).
考点1:利用“两直线平行,同位角相等”求角的度数
如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,
∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?(出示课件9)
师生共同讨论解答如下:
学生1解:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC (同位角相等,两直线平行).
学生2解:(2) ∠C =40°. ∵DE∥BC ,∴∠C = ∠AED.
(两直线平行,同位角相等)
∵∠AED=40°,∴∠C =40°.
出示课件10,学生自主练习后口答,教师订正.
2.出示课件11-12,探究两直线平行,内错角相等
教师问:在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
学生答:已知两直线平行,同位角相等,能得到内错角之间的数量关系——内错角相等.
教师问:如图,已知a//b,那么∠2与∠3相等吗?为什么
师生一起解答:
解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
总结点拨:(出示课件13)
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
教师问:你能利用几何语言描述一下平行的性质2吗?
学生答:几何语言:
∵a∥b(已知),
∴∠2=∠3 (两直线平行,内错角相等).
考点2:利用“两直线平行,内错角相等”求角的度数
如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.(出示课件14)
学生独立思考后,师生共同解答.
解:∵ a∥b(已知),
∴∠ 1= ∠ 2(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
∴∠ 2= 50° (等量代换).
出示课件15,学生自主练习后口答,教师订正.
3.出示课件16,探究两直线平行,同旁内角互补
教师问:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
学生答:已知两直线平行,能得到同旁内角之间的数量关系.
教师问:如图,已知a//b,那么∠2与∠4有什么关系呢?
学生答:已知a//b,那么∠2+∠4=180°.
教师问:你能给出证明吗?
师生一起解答:
解: ∵a//b (已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠1+∠4=180°(邻补角的性质),
∴∠2+∠4=180°(等量代换).
总结点拨:(出示课件17)
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
教师问:你能利用几何语言描述一下平行的性质2吗?
学生答:几何语言:
∵a∥b(已知),
∴∠2+∠4=180 °(两直线平行,同旁内角互补).
考点3:利用“两直线平行,同旁内角互补”求角的度数
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?(出示课件18)
学生独立思考后,师生共同解答.
解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
∴梯形的另外两个角分别是80°、65°.
出示课件19,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件20-27)
练习课件第20-27页题目,约用时20分钟.
(四)课堂小结(出示课件28)
判定两条直线平行的方法有:
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
两条直线平行的性质有:
1两直线平行,同位角相等
2.两直线平行,内错角相等
3.两直线平行,同旁内角互补
(五)课前预习
预习下节课(5.3.1第2课时)的相关内容.
会用平行线的性质和判定解决实际问题.
七、课后作业
教材第20页练习第1,2题.
八、板书设计:
平行线的性质
1.平行线的性质:
平行线性质1 : 两直线平行,同位角相等.
平行线性质2 :两直线平行,内错角相等 .
性质3:两直线平行,同旁内角互补 .
2.考点讲解
考点1 考点2 考点3
九、教学反思:
我自认为这节课上的比较成功
成功之处:
1、利用了多媒体手段,不但活跃课堂,而且提高了学生的参与面,短、频、快的大容量课堂节奏,有效的吸引并集中了学生的注意力,从而提高了学习的效益,为后面两个变形、变式、写过程题的解决奠定了基础.
2、数学课堂上教师应要强化分层次与辅导,通过分层次教学和辅导提高了学生的成绩.从对象上,要重点关注该科明显薄弱的学生,采用教师定学生、学生结对辅导等有效形式,使学生随时能得到教师的辅导同学的帮助.从方法上,要抓住学生学习的薄弱点,有针对性辅导。做到缺什么、补什么.如:第一题和第二题提问差生,第三、第四、第五题提问中等生,从而增强荣誉感,激发学习数学的信心.我觉得达到了预期的效果.
不足之处:
1、数学课堂千变万化,我虽有二十几年的教学经验,但本节课还是有诸多不足之处.首先教法不灵活,对学生不懂得的问题总觉得引导启发的不够.对教学生的自主学习,合作学习,缺乏理论指导,小组讨论时总有同学特别被动.
2、由于对学生的了解不够,对学生的学习态度、思维能力不太清楚。上课该讲的都讲了,学生掌握的情况怎样,教师心中无数.
3、如果让我重新上这节课的话,一定比现在要效果好.
11 / 13
第1课时
一、教学目标
【知识与技能】
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
【过程与方法】
经历观察,猜想,操作,交流,归纳,推理等活动,培养学生的概括能力和逻辑思维能力.
【情感态度与价值观】
通过学生动手操作,观察来发展学生的空间观念,培养及主动探索和合作能力.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
平行线的性质,区分平行线的判定方法和性质.
【教学难点】
区分平行线的判定方法和性质.
五、课前准备
教师:课件、三角尺、直尺、量角器等.
学生:三角尺、铅笔、量角器、练习本.
六、教学过程
(一)导入新课(出示课件2)
【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
(二)探索新知
1.出示课件4-7,探究两直线平行,同位角相等
教师问:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
教师依次展示学生答案:
学生1答:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120° °
角 ∠5 ∠6 ∠7 ∠8
度数
学生2答:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120°
角 ∠5 ∠6 ∠7 ∠8
度数
学生3答:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120°
学生4答:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120°
教师总结如下:如下表:
角 ∠1 ∠2 ∠3 ∠4
度数 60° 120° 60° 120°
角 ∠5 ∠6 ∠7 ∠8
度数 60° 120° 60° 120°
教师问:∠1~ ∠8中,哪些是同位角?
学生答:同位角有:∠1和∠5,∠4和∠8,∠2和∠6,∠3和∠7.
教师问:同位角的度数之间有什么关系?
学生答:同位角的度数相等.
教师问:由此你得到什么猜想?
学生答:同位角的度数相等.
教师问:再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?如下图:
学生测量后答:成立.
教师问:如果两直线不平行,上述结论还成立吗?如下图:
学生答:不相等.
教师问:请你猜想一下,什么情况下同位角相等?
学生答:猜想:两条平行线被第三条直线所截,同位角相等.
教师总结点拨:(出示课件8)
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
教师问:你能利用几何语言描述一下上面的性质吗?
学生答:几何语言:
∵a∥b(已知),
∴∠1=∠2 (两直线平行,同位角相等).
考点1:利用“两直线平行,同位角相等”求角的度数
如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,
∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?(出示课件9)
师生共同讨论解答如下:
学生1解:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC (同位角相等,两直线平行).
学生2解:(2) ∠C =40°. ∵DE∥BC ,∴∠C = ∠AED.
(两直线平行,同位角相等)
∵∠AED=40°,∴∠C =40°.
出示课件10,学生自主练习后口答,教师订正.
2.出示课件11-12,探究两直线平行,内错角相等
教师问:在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
学生答:已知两直线平行,同位角相等,能得到内错角之间的数量关系——内错角相等.
教师问:如图,已知a//b,那么∠2与∠3相等吗?为什么
师生一起解答:
解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
总结点拨:(出示课件13)
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
教师问:你能利用几何语言描述一下平行的性质2吗?
学生答:几何语言:
∵a∥b(已知),
∴∠2=∠3 (两直线平行,内错角相等).
考点2:利用“两直线平行,内错角相等”求角的度数
如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.(出示课件14)
学生独立思考后,师生共同解答.
解:∵ a∥b(已知),
∴∠ 1= ∠ 2(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
∴∠ 2= 50° (等量代换).
出示课件15,学生自主练习后口答,教师订正.
3.出示课件16,探究两直线平行,同旁内角互补
教师问:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
学生答:已知两直线平行,能得到同旁内角之间的数量关系.
教师问:如图,已知a//b,那么∠2与∠4有什么关系呢?
学生答:已知a//b,那么∠2+∠4=180°.
教师问:你能给出证明吗?
师生一起解答:
解: ∵a//b (已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠1+∠4=180°(邻补角的性质),
∴∠2+∠4=180°(等量代换).
总结点拨:(出示课件17)
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
教师问:你能利用几何语言描述一下平行的性质2吗?
学生答:几何语言:
∵a∥b(已知),
∴∠2+∠4=180 °(两直线平行,同旁内角互补).
考点3:利用“两直线平行,同旁内角互补”求角的度数
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?(出示课件18)
学生独立思考后,师生共同解答.
解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
∴梯形的另外两个角分别是80°、65°.
出示课件19,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件20-27)
练习课件第20-27页题目,约用时20分钟.
(四)课堂小结(出示课件28)
判定两条直线平行的方法有:
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
两条直线平行的性质有:
1两直线平行,同位角相等
2.两直线平行,内错角相等
3.两直线平行,同旁内角互补
(五)课前预习
预习下节课(5.3.1第2课时)的相关内容.
会用平行线的性质和判定解决实际问题.
七、课后作业
教材第20页练习第1,2题.
八、板书设计:
平行线的性质
1.平行线的性质:
平行线性质1 : 两直线平行,同位角相等.
平行线性质2 :两直线平行,内错角相等 .
性质3:两直线平行,同旁内角互补 .
2.考点讲解
考点1 考点2 考点3
九、教学反思:
我自认为这节课上的比较成功
成功之处:
1、利用了多媒体手段,不但活跃课堂,而且提高了学生的参与面,短、频、快的大容量课堂节奏,有效的吸引并集中了学生的注意力,从而提高了学习的效益,为后面两个变形、变式、写过程题的解决奠定了基础.
2、数学课堂上教师应要强化分层次与辅导,通过分层次教学和辅导提高了学生的成绩.从对象上,要重点关注该科明显薄弱的学生,采用教师定学生、学生结对辅导等有效形式,使学生随时能得到教师的辅导同学的帮助.从方法上,要抓住学生学习的薄弱点,有针对性辅导。做到缺什么、补什么.如:第一题和第二题提问差生,第三、第四、第五题提问中等生,从而增强荣誉感,激发学习数学的信心.我觉得达到了预期的效果.
不足之处:
1、数学课堂千变万化,我虽有二十几年的教学经验,但本节课还是有诸多不足之处.首先教法不灵活,对学生不懂得的问题总觉得引导启发的不够.对教学生的自主学习,合作学习,缺乏理论指导,小组讨论时总有同学特别被动.
2、由于对学生的了解不够,对学生的学习态度、思维能力不太清楚。上课该讲的都讲了,学生掌握的情况怎样,教师心中无数.
3、如果让我重新上这节课的话,一定比现在要效果好.
11 / 13
