人教版七年级数学下册5.3.1 平行线的性质(第2课时)教案
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线的性质(第2课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 85.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览


文档简介
5.3.1 平行线的性质
第2课时
一、教学目标
【知识与技能】
1.分清平行线的性质和判定,已知平行用性质,要证平行用判定.
2.进一步熟悉平行线的判定方法和性质.
3.能够综合运用平行线性质和判定进行推理证明.
【过程与方法】
1.使学生进一步学会识图,能将复杂图形分解为基本图形,会对已知条件和求证结论进行转化.
2.通过复习使学生了解分析问题的方法(分析法、综合法),初步领会化繁为简、化未知为已知的化归思想.
【情感态度与价值观】
1.通过推理论证使学生建立已知和未知间的联系。并理解数学与实际生活的联系.
2.培养学生合作交流意识和探索精神,提高学习数学的兴趣.
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
1.掌握平行线的判定和性质,并能用它们进行简单的推理或计算.
2.初步掌握分析问题和解决问题的方法.
【教学难点】
使学生将知识条理化、系统化,能正确地运用进行严密推理.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
一辆车沿AB方向行驶,在C处拐了一个弯,行驶一段时间到D处又一次改变方向,此时车子与原来的方向是否一致?为什么?
(二)探索新知
1.出示课件4,平行线性质和判定的综合应用
考点1:平行线性质和判定的综合应用
如图,已知:AD∥BC, ∠AEF=∠B,求证:AD∥EF.
师生共同讨论解答如下:
证明:∵ AD ∥BC(已知),
∴ ∠A+∠B=180°( 两直线平行,同旁内角互补).
∵ ∠AEF=∠B(已知),
∴ ∠A+∠AEF=180°(等量代换).
∴ AD∥EF(同旁内角互补,两直线平行).
出示课件5,学生自主练习后口答,教师订正.
2.出示课件6-11,探究添加辅助线的证明题
考点2:添加辅助线的证明题
教师问:如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
师生一起解答:
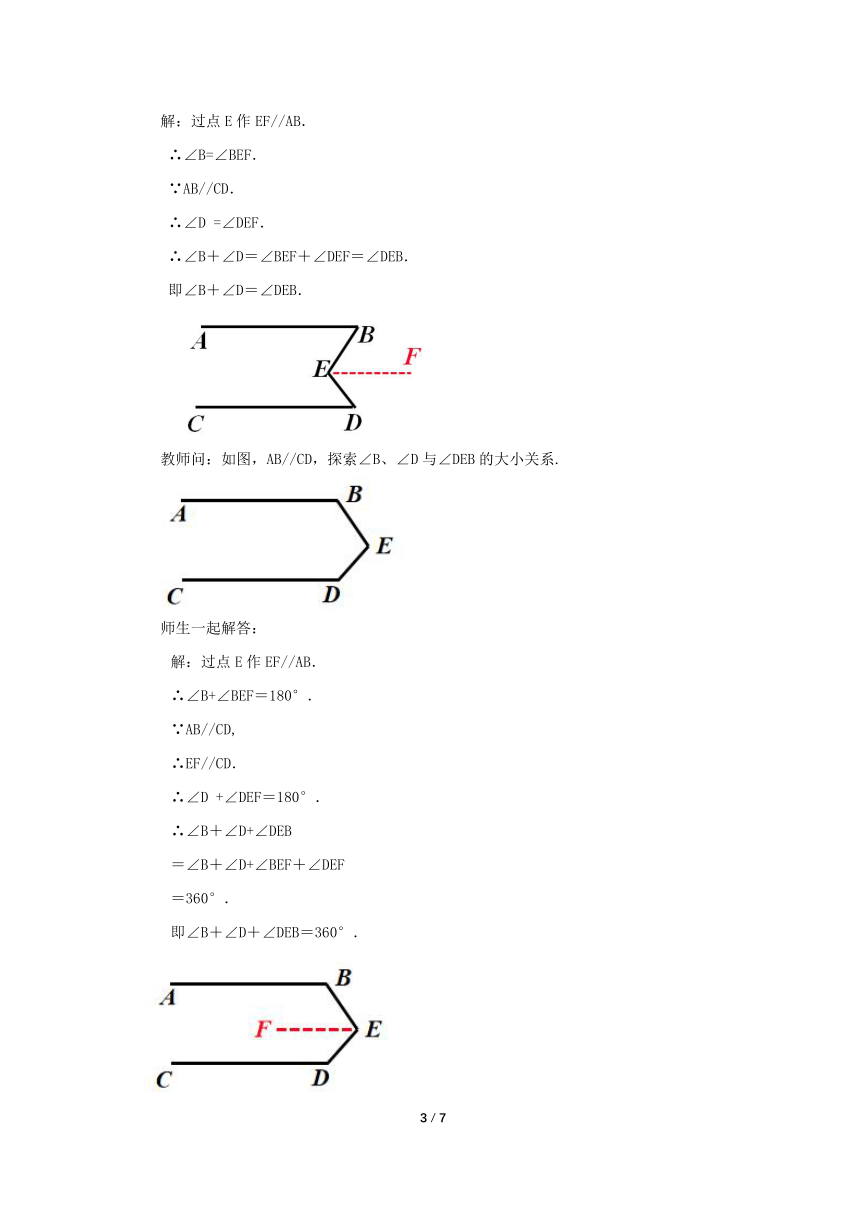
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB.
教师问:如图,AB//CD,探索∠B、∠D与∠DEB的大小关系.
师生一起解答:
解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
教师出示问题:完成下列问题:
如图,AB∥CD, ∠A+∠ E1 + ∠ E2 +∠C =______.
师生一起解答:
解:分别过点E1、E2作E1F1//AB, E2F2//AB.
∴∠A+∠AE1F1=180°.
∵E1F1//AB, E2F2//AB.
∴E1F1//E2F2
∴∠F1E1E2+∠E1E2F2=180°.
∵AB//CD,
∴E2F2//CD.
∴∠C +∠CE2F2=180°.
∴∠A+∠AE1F1+∠F1E1E2+∠E1E2F2+∠C +∠CE2F2
=∠A+∠AE1E2+∠E1E2C+∠C
=540°.
即∠A+∠ E1 + ∠ E2 +∠C =540°.
教师问:如图,AB∥CD, ∠A+∠ E1 + ∠ E2 +∠E3+∠C =______.
学生答:如图所示:∠A+∠ E1 + ∠ E2 +∠E3+∠C =720°.
师生一起小结:如图,AB∥CD,则 :
当有一个拐点时: ∠A+∠E+∠C= 360°.
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
教师问:若有n个拐点,你能找到规律吗?
学生答:当有n个拐点时:
∠A+∠ E1 + ∠ E2 +…+∠En +∠C = 180°(n+1)
教师问:如图,若AB∥CD, 则:
师生一起解答:
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
当左边有三个角,右边有两个角时:
∠A+∠ F1 +∠C = ∠ E1 +∠ E2
教师问:若左边有n个角,右边有m个角,你能找到规律吗?
学生答:当左边有n个角,右边有m个角时:
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1=∠E1+∠E2 +…+∠Em-1+∠D
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件12-18)
练习课件第12-18页题目,约用时20分钟.
(四)课堂小结(出示课件19)
平行线的判定与性质
平行线的判定 已知角的关系得平行的关系.
平行线的性质 已知平行的关系得角的关系.
(五)课前预习
预习下节课(5.3.2第1课时)的相关内容.
知道命题、真命题、假命题、定理、证明的定义
七、课后作业
教材第22页习题5.3第1,2,5题.
八、板书设计:
1.知识梳理
两直线平行
2.考点讲解
考点1 考点2
九、教学反思:
成功之处:本节内容的重点是平行线的性质及判定的综合,直接运用了“∵”“∴”的推理形式,为学生创设了一个学习推理的环境,逐步培养学生的逻辑推理能力.因此,这一节课有着承上启下的作用,比较重要.本节内容的难点是理解平行线的性质和判定的区别,并在推理中正确地应用.由于学生还没有学习命题的概念和命题的组成,不知道判定和性质的本质区别和联系是什么,所以在教学中,应让学生通过应用和讨论,体会到如果已知角的关系,推出两直线平行,就是平行线的判定;反之,如果两直线平行,得出角的关系,就是平行线的性质.
不足之处:学生利用“∵”“∴”进行推理容易混淆,要注意分析这两个符号的不同点,让学生尽快去分开,熟练应用.
8 / 9
第2课时
一、教学目标
【知识与技能】
1.分清平行线的性质和判定,已知平行用性质,要证平行用判定.
2.进一步熟悉平行线的判定方法和性质.
3.能够综合运用平行线性质和判定进行推理证明.
【过程与方法】
1.使学生进一步学会识图,能将复杂图形分解为基本图形,会对已知条件和求证结论进行转化.
2.通过复习使学生了解分析问题的方法(分析法、综合法),初步领会化繁为简、化未知为已知的化归思想.
【情感态度与价值观】
1.通过推理论证使学生建立已知和未知间的联系。并理解数学与实际生活的联系.
2.培养学生合作交流意识和探索精神,提高学习数学的兴趣.
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
1.掌握平行线的判定和性质,并能用它们进行简单的推理或计算.
2.初步掌握分析问题和解决问题的方法.
【教学难点】
使学生将知识条理化、系统化,能正确地运用进行严密推理.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
一辆车沿AB方向行驶,在C处拐了一个弯,行驶一段时间到D处又一次改变方向,此时车子与原来的方向是否一致?为什么?
(二)探索新知
1.出示课件4,平行线性质和判定的综合应用
考点1:平行线性质和判定的综合应用
如图,已知:AD∥BC, ∠AEF=∠B,求证:AD∥EF.
师生共同讨论解答如下:
证明:∵ AD ∥BC(已知),
∴ ∠A+∠B=180°( 两直线平行,同旁内角互补).
∵ ∠AEF=∠B(已知),
∴ ∠A+∠AEF=180°(等量代换).
∴ AD∥EF(同旁内角互补,两直线平行).
出示课件5,学生自主练习后口答,教师订正.
2.出示课件6-11,探究添加辅助线的证明题
考点2:添加辅助线的证明题
教师问:如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
师生一起解答:
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB.
教师问:如图,AB//CD,探索∠B、∠D与∠DEB的大小关系.
师生一起解答:
解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
教师出示问题:完成下列问题:
如图,AB∥CD, ∠A+∠ E1 + ∠ E2 +∠C =______.
师生一起解答:
解:分别过点E1、E2作E1F1//AB, E2F2//AB.
∴∠A+∠AE1F1=180°.
∵E1F1//AB, E2F2//AB.
∴E1F1//E2F2
∴∠F1E1E2+∠E1E2F2=180°.
∵AB//CD,
∴E2F2//CD.
∴∠C +∠CE2F2=180°.
∴∠A+∠AE1F1+∠F1E1E2+∠E1E2F2+∠C +∠CE2F2
=∠A+∠AE1E2+∠E1E2C+∠C
=540°.
即∠A+∠ E1 + ∠ E2 +∠C =540°.
教师问:如图,AB∥CD, ∠A+∠ E1 + ∠ E2 +∠E3+∠C =______.
学生答:如图所示:∠A+∠ E1 + ∠ E2 +∠E3+∠C =720°.
师生一起小结:如图,AB∥CD,则 :
当有一个拐点时: ∠A+∠E+∠C= 360°.
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
教师问:若有n个拐点,你能找到规律吗?
学生答:当有n个拐点时:
∠A+∠ E1 + ∠ E2 +…+∠En +∠C = 180°(n+1)
教师问:如图,若AB∥CD, 则:
师生一起解答:
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
当左边有三个角,右边有两个角时:
∠A+∠ F1 +∠C = ∠ E1 +∠ E2
教师问:若左边有n个角,右边有m个角,你能找到规律吗?
学生答:当左边有n个角,右边有m个角时:
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1=∠E1+∠E2 +…+∠Em-1+∠D
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件12-18)
练习课件第12-18页题目,约用时20分钟.
(四)课堂小结(出示课件19)
平行线的判定与性质
平行线的判定 已知角的关系得平行的关系.
平行线的性质 已知平行的关系得角的关系.
(五)课前预习
预习下节课(5.3.2第1课时)的相关内容.
知道命题、真命题、假命题、定理、证明的定义
七、课后作业
教材第22页习题5.3第1,2,5题.
八、板书设计:
1.知识梳理
两直线平行
2.考点讲解
考点1 考点2
九、教学反思:
成功之处:本节内容的重点是平行线的性质及判定的综合,直接运用了“∵”“∴”的推理形式,为学生创设了一个学习推理的环境,逐步培养学生的逻辑推理能力.因此,这一节课有着承上启下的作用,比较重要.本节内容的难点是理解平行线的性质和判定的区别,并在推理中正确地应用.由于学生还没有学习命题的概念和命题的组成,不知道判定和性质的本质区别和联系是什么,所以在教学中,应让学生通过应用和讨论,体会到如果已知角的关系,推出两直线平行,就是平行线的判定;反之,如果两直线平行,得出角的关系,就是平行线的性质.
不足之处:学生利用“∵”“∴”进行推理容易混淆,要注意分析这两个符号的不同点,让学生尽快去分开,熟练应用.
8 / 9
