人教版七年级数学下册 5.4 平移 教案
文档属性
| 名称 | 人教版七年级数学下册 5.4 平移 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 751.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览




文档简介
5.4 平移
一、教学目标
【知识与技能】
1.通过实例认识平移,理解平移的含义和性质.
2.会找出平移前后图形中对应点和对应线段.
3.能按要求作出简单平面图形平移后的图形,培养观察和动手操作的能力.
【过程与方法】
经历操作、探究、归纳和总结平移性质的过程,感受数学知识的发生和发展,培养学生的抽象概括能力;体会从数学的角度理解问题,提高综合运用所学知识和技能解决问题的水平.
【情感态度与价值观】
通过丰富多彩的活动,让学生感受数学充满了探索性与创造性,激发学生的探究热情,并培养学生良好的团队合作意识和创新精神.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
能按要求作出平移后的图形.
【教学难点】
理解并掌握平移的性质.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
如图,传送带上的电视机在运送过程中发生了什么变化?
(二)探索新知
1.出示课件4-8,探究平移的有关概念
教师问:仔细观察下列美丽的图案,回答问题:这些图案有什么共同特点?
学生答:都是由一个简单图案组成的.
教师问:上面这些图案能否根据其中一部分绘制整个图案?若能,你能想象出是怎么绘制的吗?
学生答:上面这些图案能根据其中一部分绘制整个图案,经过上下,左右移动就可以得到.
教师问:如何在一张半透明的纸上,画出一排形状和大小如右图的雪人呢?
学生答:可以把半透明的纸盖在上图上,先描出一个雪人,然后按同一个方向陆续移动这张纸,再描出第二个,第三个……
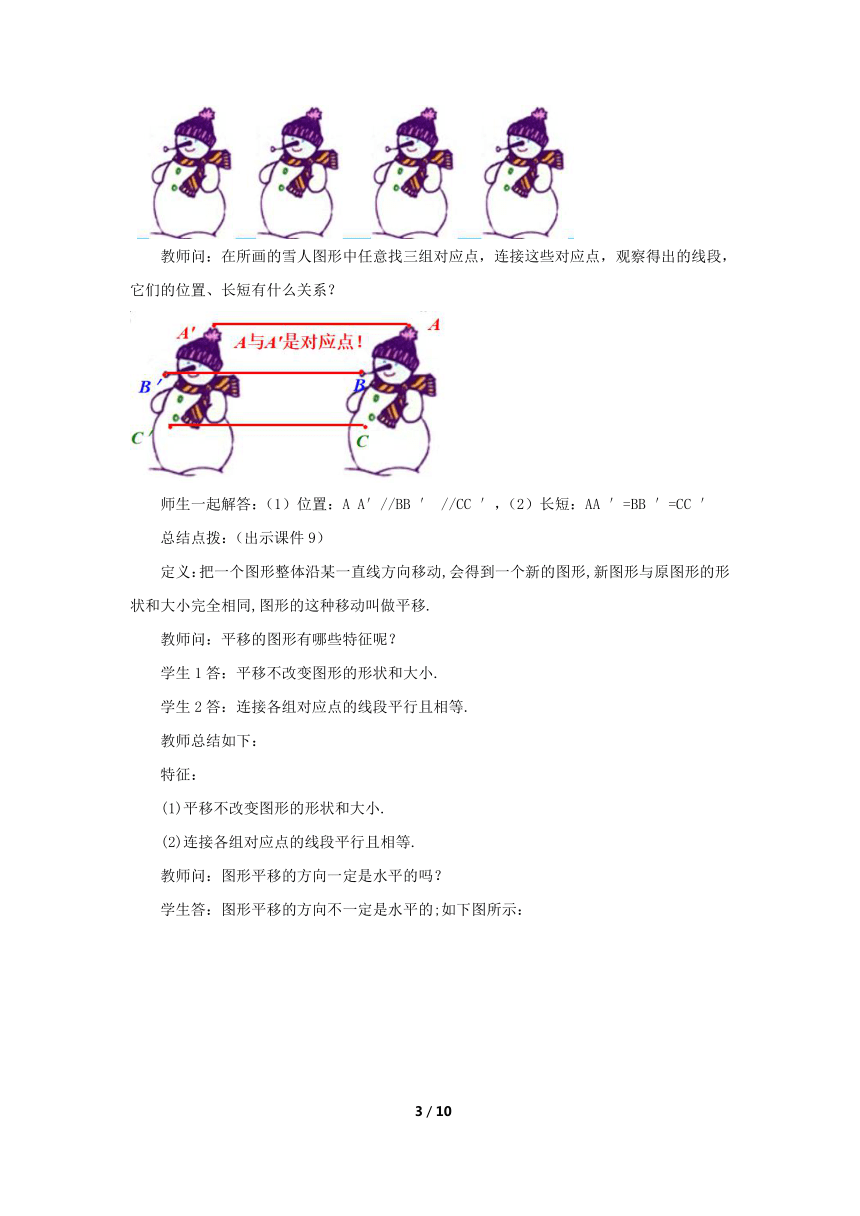
教师问:在所画的雪人图形中任意找三组对应点,连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
师生一起解答:(1)位置:A A′//BB ′ //CC ′,(2)长短:AA ′=BB ′=CC ′
总结点拨:(出示课件9)
定义:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.
教师问:平移的图形有哪些特征呢?
学生1答:平移不改变图形的形状和大小.
学生2答:连接各组对应点的线段平行且相等.
教师总结如下:
特征:
(1)平移不改变图形的形状和大小.
(2)连接各组对应点的线段平行且相等.
教师问:图形平移的方向一定是水平的吗?
学生答:图形平移的方向不一定是水平的;如下图所示:
教师问:图形平移的位置由什么确定
学生答:图形平移的位置由平移的方向和距离决定.
总结归纳:(出示课件11)
(1)平移只改变图形的位置,不改变图形的形状、大小、方向.
(2)平移的方向可以是任意的,只要是直线方向即可.
(3)图形的平移是整个图形都在移动,即图形中所有的点、线平移的方向、距离都相同.
(4)确定一个图形平移的方向和距离,只需确定其上一个点平移的方向和距离即可.
考点1:平移现象的识别
下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.(出示课件12)
师生共同讨论解答如下:
解析:选项(3)、(5)中图形的所有点不是沿同一方向运动,所以不是平移.选项(1)、(2)、(4)符合平移的条件.
答案:(1)、(2)、(4)
总结点拨:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,只是位置发生变化.注意平移是图形整体沿某一直线方向移动.图形绕某一点的旋转不是平移.
出示课件13,学生自主练习后口答,教师订正.
考点2:图形平移变换的识别
下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )(出示课件14)
B. C. D.
学生独立思考后,师生共同解答.
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
答案:A.
总结点拨:
本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,同学们容易混淆图形的平移与旋转或翻转,以致选错.
出示课件15,学生自主练习后口答,教师订正.
2.出示课件16-17,探究平移的性质
教师问:已知直线PQ和直线外一点A、D,作出直线AB∥DE,AC∥DF.
学生答:如图所示,利用直尺和三角板作图,根据一放,二靠,三移,四画,作出图形(出示课件16)
教师问:直尺PQ是倾斜放置,用三角板能否画出平行线?
学生答:可以画出平行的直线,只要同位角相等就可以.
教师问:线段AB与DE的位置关系与数量关系是怎样的呢?
学生答:AB=DE,AB//DE.
教师问:观察:线段AC与DF的位置关系与数量关系是怎样的呢?
学生答:AC=DF, AC//DF.
教师问:观察:线段BC与EF的位置关系与数量关系是怎样的呢?
学生答:BC=EF,CB和EF在一条直线上.
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
教师问:通过上面图形的观察,你能说一说平移的性质吗?
学生1答:平移后的图形与原来的图形的对应线段平行且相等.
学生2答:在平移过程中,对应线段也可能在一条直线上,如BC与EF.
学生3答:平移后图形的形状与大小都没有变化.
学生4答:平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
教师总结归纳:(出示课件17)
规律小结
1.平移后的图形与原来的图形的对应线段平行且相等;
2.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3.平移后图形的形状与大小都没有变化;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
教师问:三角形ABC沿着PQ的方向平移到 △A'B'C'的位置,除了对应线段平行且相等外,你还发现了什么现象?(出示课件18)
学生答:对应点移动的距离相等.
教师问:BC的中点M平移到什么地方去了?
学生答:BC的中点M平移到线段B'C'的中点M',也移动到线段B"C"的中点M"的位置.
教师问:平移的图形有哪些性质呢?
教师依次展示学生答案:
学生1答:平移的两个图形形状和大小完全相同.
学生2答:对应线段平行(或在同一直线上)且相等.
学生3答:各对应点所连线段平行(或在同一直线上)且相等.
教师总结点拨:(出示课件19)
图形平移的基本性质:
①平移的两个图形形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等.
教师问:你能利用几何语言描述一下平移的性质吗?
教师依次展示学生解答过程
学生1答:∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,BC ∥EF(或共线).
学生2答:∵三角形ABC平移得到三角形DEF,
∴AB=DE,AC=DF,BC=EF.
学生3答:∵三角形ABC平移得到三角形DEF,
∴AD∥BE∥CF(或共线).
学生4答:∵三角形ABC平移得到三角形DEF,
∴AD=BE=CF.
教师总结如下:
几何符号语言:
∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,
BC∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
考点3:平移作图
如图,平移三角形ABC,使点A移动到点A',画出平移后的三角形A'B'C'.(出示课件20)
学生独立思考后,师生共同解答.
解:(1)连接AA',
(2)过点B作AA'的平行线, 在上截取BB'= AA',
(3)过点C作AA'的平行线,在上截取CC'= AA',
(4)连接A'B',B'C',A'C',所得的三角形就是平移后的
三角形.
总结点拨:(1)平移的作图要注意两个方面:平移的方向和平移的距离;(2)作直线型图形平移后的图形,关键是作出点平移后的对应点.
总结归纳:(出示课件21)
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
出示课件22,学生自主练习,教师给出答案.
考点4:利用平移求面积
如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少 (出示课件23)
学生独立思考后,师生共同解答.
提示:有两种平移方式.
解:长草部分的面积=(21-1)×(15-1)=280(m2).
思考:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形.
学生独立思考后,师生共同解答.
解:长草部分的面积=(21-1)×15=300(m2).
出示课件25,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件26-35)
练习课件第26-35页题目,约用时20分钟.
(四)课堂小结(出示课件36)
平移的概念 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的性质 1.平移前后图形的形状和大小完全相同; 2.对应线段平行(或在同一直线上)且相等; 3.各对应点所连线段平行(或在同一直线上)且相等.
平移作图 1.关键在于按要求作出对应点; 2.然后,顺次连接对应点即可.
(五)课前预习
预习下节课(6.1第1课时)的相关内容.
知道算术平方根、被开方数的定义和0的算术平方根.
七、课后作业
教材第30页习题5.4第1,2题.
八、板书设计
1.知识梳理
平移
2.考点讲解
考点1 考点2 考点3 考点4
九、教学反思
成功之处:本节课通过生活中的实例引入平移的概念,在学习中,引导学生分析、观察、概括得出平移的性质,并通过例题和练习加深对平移性质的理解.让学生作图,自主探究.平移的作图是本节课的重点,应让学生加强训练,结合解题中的错误分析原因,举一反三.
不足之处:在课堂上放手让学生小组讨论的内容太少,对学生总是不放心,应该大胆放手,让学生多讨论多动手多动脑,这样才能提高学生学习的积极性.
1 / 13
一、教学目标
【知识与技能】
1.通过实例认识平移,理解平移的含义和性质.
2.会找出平移前后图形中对应点和对应线段.
3.能按要求作出简单平面图形平移后的图形,培养观察和动手操作的能力.
【过程与方法】
经历操作、探究、归纳和总结平移性质的过程,感受数学知识的发生和发展,培养学生的抽象概括能力;体会从数学的角度理解问题,提高综合运用所学知识和技能解决问题的水平.
【情感态度与价值观】
通过丰富多彩的活动,让学生感受数学充满了探索性与创造性,激发学生的探究热情,并培养学生良好的团队合作意识和创新精神.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
能按要求作出平移后的图形.
【教学难点】
理解并掌握平移的性质.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
如图,传送带上的电视机在运送过程中发生了什么变化?
(二)探索新知
1.出示课件4-8,探究平移的有关概念
教师问:仔细观察下列美丽的图案,回答问题:这些图案有什么共同特点?
学生答:都是由一个简单图案组成的.
教师问:上面这些图案能否根据其中一部分绘制整个图案?若能,你能想象出是怎么绘制的吗?
学生答:上面这些图案能根据其中一部分绘制整个图案,经过上下,左右移动就可以得到.
教师问:如何在一张半透明的纸上,画出一排形状和大小如右图的雪人呢?
学生答:可以把半透明的纸盖在上图上,先描出一个雪人,然后按同一个方向陆续移动这张纸,再描出第二个,第三个……
教师问:在所画的雪人图形中任意找三组对应点,连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
师生一起解答:(1)位置:A A′//BB ′ //CC ′,(2)长短:AA ′=BB ′=CC ′
总结点拨:(出示课件9)
定义:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.
教师问:平移的图形有哪些特征呢?
学生1答:平移不改变图形的形状和大小.
学生2答:连接各组对应点的线段平行且相等.
教师总结如下:
特征:
(1)平移不改变图形的形状和大小.
(2)连接各组对应点的线段平行且相等.
教师问:图形平移的方向一定是水平的吗?
学生答:图形平移的方向不一定是水平的;如下图所示:
教师问:图形平移的位置由什么确定
学生答:图形平移的位置由平移的方向和距离决定.
总结归纳:(出示课件11)
(1)平移只改变图形的位置,不改变图形的形状、大小、方向.
(2)平移的方向可以是任意的,只要是直线方向即可.
(3)图形的平移是整个图形都在移动,即图形中所有的点、线平移的方向、距离都相同.
(4)确定一个图形平移的方向和距离,只需确定其上一个点平移的方向和距离即可.
考点1:平移现象的识别
下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.(出示课件12)
师生共同讨论解答如下:
解析:选项(3)、(5)中图形的所有点不是沿同一方向运动,所以不是平移.选项(1)、(2)、(4)符合平移的条件.
答案:(1)、(2)、(4)
总结点拨:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,只是位置发生变化.注意平移是图形整体沿某一直线方向移动.图形绕某一点的旋转不是平移.
出示课件13,学生自主练习后口答,教师订正.
考点2:图形平移变换的识别
下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )(出示课件14)
B. C. D.
学生独立思考后,师生共同解答.
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
答案:A.
总结点拨:
本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,同学们容易混淆图形的平移与旋转或翻转,以致选错.
出示课件15,学生自主练习后口答,教师订正.
2.出示课件16-17,探究平移的性质
教师问:已知直线PQ和直线外一点A、D,作出直线AB∥DE,AC∥DF.
学生答:如图所示,利用直尺和三角板作图,根据一放,二靠,三移,四画,作出图形(出示课件16)
教师问:直尺PQ是倾斜放置,用三角板能否画出平行线?
学生答:可以画出平行的直线,只要同位角相等就可以.
教师问:线段AB与DE的位置关系与数量关系是怎样的呢?
学生答:AB=DE,AB//DE.
教师问:观察:线段AC与DF的位置关系与数量关系是怎样的呢?
学生答:AC=DF, AC//DF.
教师问:观察:线段BC与EF的位置关系与数量关系是怎样的呢?
学生答:BC=EF,CB和EF在一条直线上.
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
教师问:通过上面图形的观察,你能说一说平移的性质吗?
学生1答:平移后的图形与原来的图形的对应线段平行且相等.
学生2答:在平移过程中,对应线段也可能在一条直线上,如BC与EF.
学生3答:平移后图形的形状与大小都没有变化.
学生4答:平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
教师总结归纳:(出示课件17)
规律小结
1.平移后的图形与原来的图形的对应线段平行且相等;
2.在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3.平移后图形的形状与大小都没有变化;
4.平移的方向是直尺PQ倾斜放置的方向,平移的距离是BE的长度.
教师问:三角形ABC沿着PQ的方向平移到 △A'B'C'的位置,除了对应线段平行且相等外,你还发现了什么现象?(出示课件18)
学生答:对应点移动的距离相等.
教师问:BC的中点M平移到什么地方去了?
学生答:BC的中点M平移到线段B'C'的中点M',也移动到线段B"C"的中点M"的位置.
教师问:平移的图形有哪些性质呢?
教师依次展示学生答案:
学生1答:平移的两个图形形状和大小完全相同.
学生2答:对应线段平行(或在同一直线上)且相等.
学生3答:各对应点所连线段平行(或在同一直线上)且相等.
教师总结点拨:(出示课件19)
图形平移的基本性质:
①平移的两个图形形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等.
教师问:你能利用几何语言描述一下平移的性质吗?
教师依次展示学生解答过程
学生1答:∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,BC ∥EF(或共线).
学生2答:∵三角形ABC平移得到三角形DEF,
∴AB=DE,AC=DF,BC=EF.
学生3答:∵三角形ABC平移得到三角形DEF,
∴AD∥BE∥CF(或共线).
学生4答:∵三角形ABC平移得到三角形DEF,
∴AD=BE=CF.
教师总结如下:
几何符号语言:
∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,
BC∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
考点3:平移作图
如图,平移三角形ABC,使点A移动到点A',画出平移后的三角形A'B'C'.(出示课件20)
学生独立思考后,师生共同解答.
解:(1)连接AA',
(2)过点B作AA'的平行线, 在上截取BB'= AA',
(3)过点C作AA'的平行线,在上截取CC'= AA',
(4)连接A'B',B'C',A'C',所得的三角形就是平移后的
三角形.
总结点拨:(1)平移的作图要注意两个方面:平移的方向和平移的距离;(2)作直线型图形平移后的图形,关键是作出点平移后的对应点.
总结归纳:(出示课件21)
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
出示课件22,学生自主练习,教师给出答案.
考点4:利用平移求面积
如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少 (出示课件23)
学生独立思考后,师生共同解答.
提示:有两种平移方式.
解:长草部分的面积=(21-1)×(15-1)=280(m2).
思考:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形.
学生独立思考后,师生共同解答.
解:长草部分的面积=(21-1)×15=300(m2).
出示课件25,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件26-35)
练习课件第26-35页题目,约用时20分钟.
(四)课堂小结(出示课件36)
平移的概念 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的性质 1.平移前后图形的形状和大小完全相同; 2.对应线段平行(或在同一直线上)且相等; 3.各对应点所连线段平行(或在同一直线上)且相等.
平移作图 1.关键在于按要求作出对应点; 2.然后,顺次连接对应点即可.
(五)课前预习
预习下节课(6.1第1课时)的相关内容.
知道算术平方根、被开方数的定义和0的算术平方根.
七、课后作业
教材第30页习题5.4第1,2题.
八、板书设计
1.知识梳理
平移
2.考点讲解
考点1 考点2 考点3 考点4
九、教学反思
成功之处:本节课通过生活中的实例引入平移的概念,在学习中,引导学生分析、观察、概括得出平移的性质,并通过例题和练习加深对平移性质的理解.让学生作图,自主探究.平移的作图是本节课的重点,应让学生加强训练,结合解题中的错误分析原因,举一反三.
不足之处:在课堂上放手让学生小组讨论的内容太少,对学生总是不放心,应该大胆放手,让学生多讨论多动手多动脑,这样才能提高学生学习的积极性.
1 / 13
