人教版七年级数学下册7.1.2 平面直角坐标系 教案
文档属性
| 名称 | 人教版七年级数学下册7.1.2 平面直角坐标系 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:30:40 | ||
图片预览


文档简介
7.1.2 平面直角坐标系
一、教学目标
【知识与技能】
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系 .
2.理解各象限内及坐标轴上点的坐标特征.
3.用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
【过程与方法】
1.经历建立直角坐标系的过程,进而理解平面直角坐标系的意义.
2.通过分析具体特例得到特殊位置点的坐标特征以及有特殊位置关系的点的坐标的特征.
3.通过小组学习等活动经历建立坐标系的过程,进一步提高学生应用已有知识与技能的基础上形成新的知识,获得新的技能,以提高解决数学问题的能力.
【情感态度与价值观】
1.让学生体会到x轴、y轴的关系,进而明白事物之间是相互联系的这一辩证思想,培养耐心细致的良好学习作风.
2通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认同他人.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
平面直角坐标系的意义,由坐标找点,由点找坐标.
【教学难点】
平面直角坐标系内的点与有序数对一一对应的关系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
神舟九号、七号、六号和五号等卫星发射成功,圆了几代中国人的梦想,让全中国人为之骄傲和自豪!但是你们知道我们的科学家是怎样迅速地找到返回舱着陆的位置的吗?这就要依赖于GPS——卫星全球定位系统”.大家一定觉得很神奇吧!学习了今天的内容,你就会明白其中的奥妙.
(二)探索新知
1.出示课件4-9,探究平面直角坐标系的有关概念
教师问: 如何确定直线上点的位置?
学生答: 在直线上规定了原点、正方向、单位长度就构成了数轴.
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.
教师问:知道数轴上一点的坐标,能确定这个点的位置吗?
学生答:知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.例如在数轴上,坐标为2的点是B.
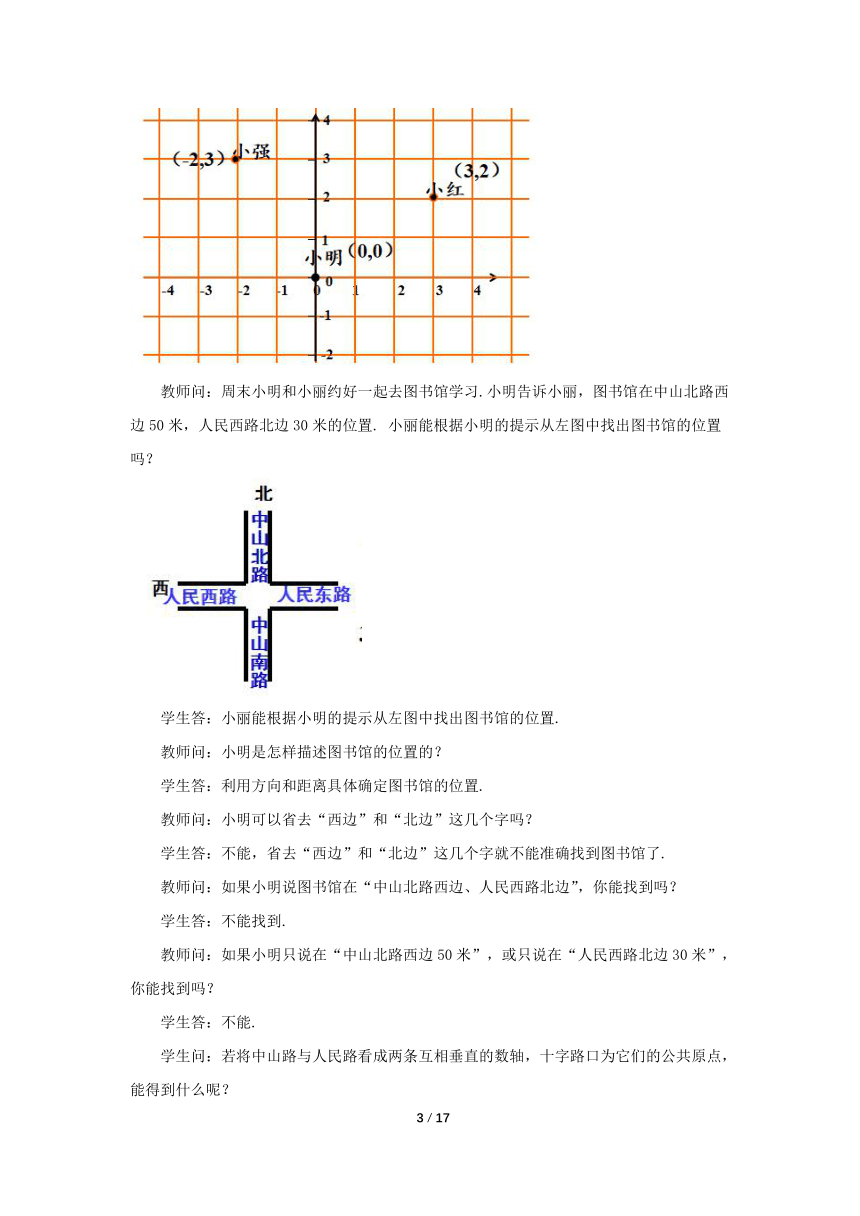
教师问:如何确定平面上点的位置?如下图:小强、小红、小明家的位置?
师生一起解答:利用两个数轴,使这两条数轴互相垂直,可以确定位置,如下图所示:
教师问:周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置. 小丽能根据小明的提示从左图中找出图书馆的位置吗?
学生答:小丽能根据小明的提示从左图中找出图书馆的位置.
教师问:小明是怎样描述图书馆的位置的?
学生答:利用方向和距离具体确定图书馆的位置.
教师问:小明可以省去“西边”和“北边”这几个字吗?
学生答:不能,省去“西边”和“北边”这几个字就不能准确找到图书馆了.
教师问:如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
学生答:不能找到.
教师问:如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
学生答:不能.
学生问:若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,能得到什么呢?
教师答:若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
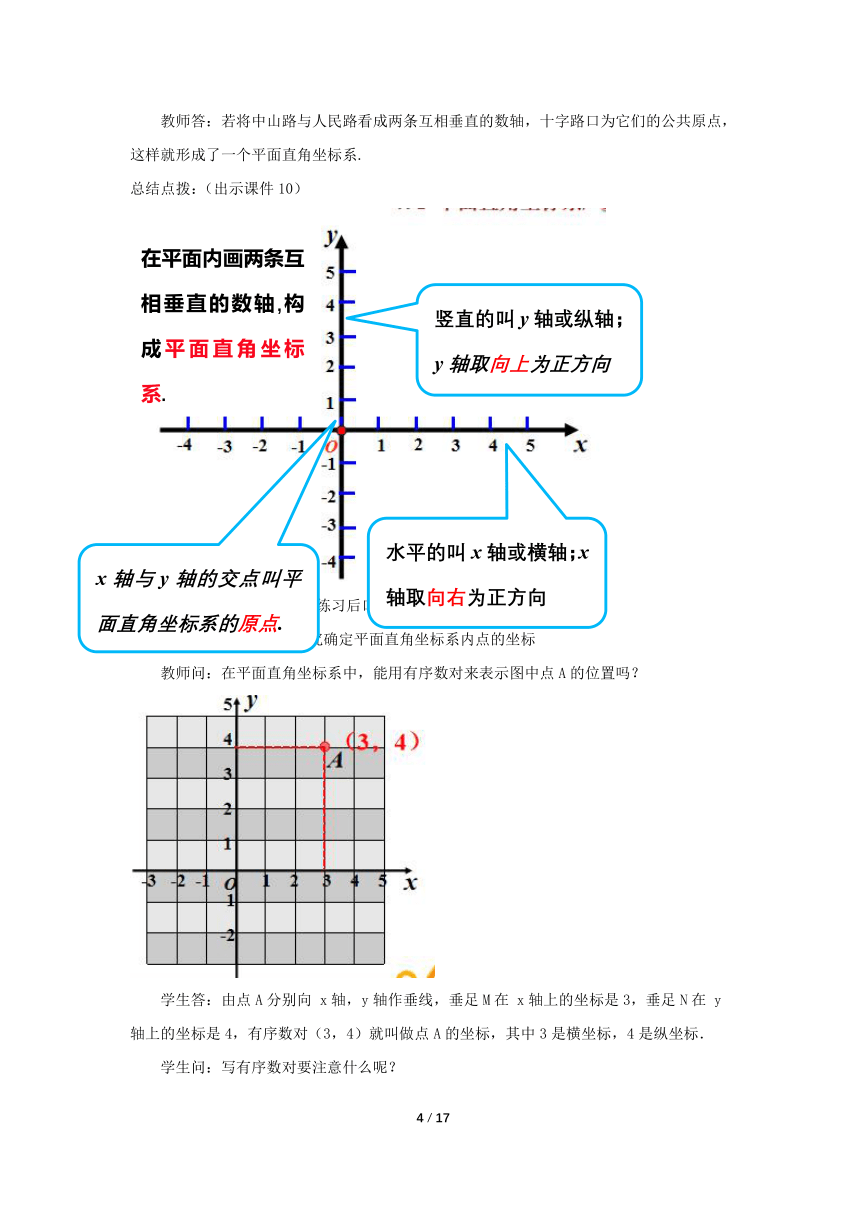
总结点拨:(出示课件10)
出示课件11,学生自主练习后口答,教师订正.
2.出示课件12-14,探究确定平面直角坐标系内点的坐标
教师问:在平面直角坐标系中,能用有序数对来表示图中点A的位置吗?
学生答:由点A分别向 x轴,y轴作垂线,垂足M在 x轴上的坐标是3,垂足N在 y轴上的坐标是4,有序数对(3,4)就叫做点A的坐标,其中3是横坐标,4是纵坐标.
学生问:写有序数对要注意什么呢?
教师答:注意:表示点的坐标时,必须横坐标在前,纵坐标在后,中间用逗号隔开.
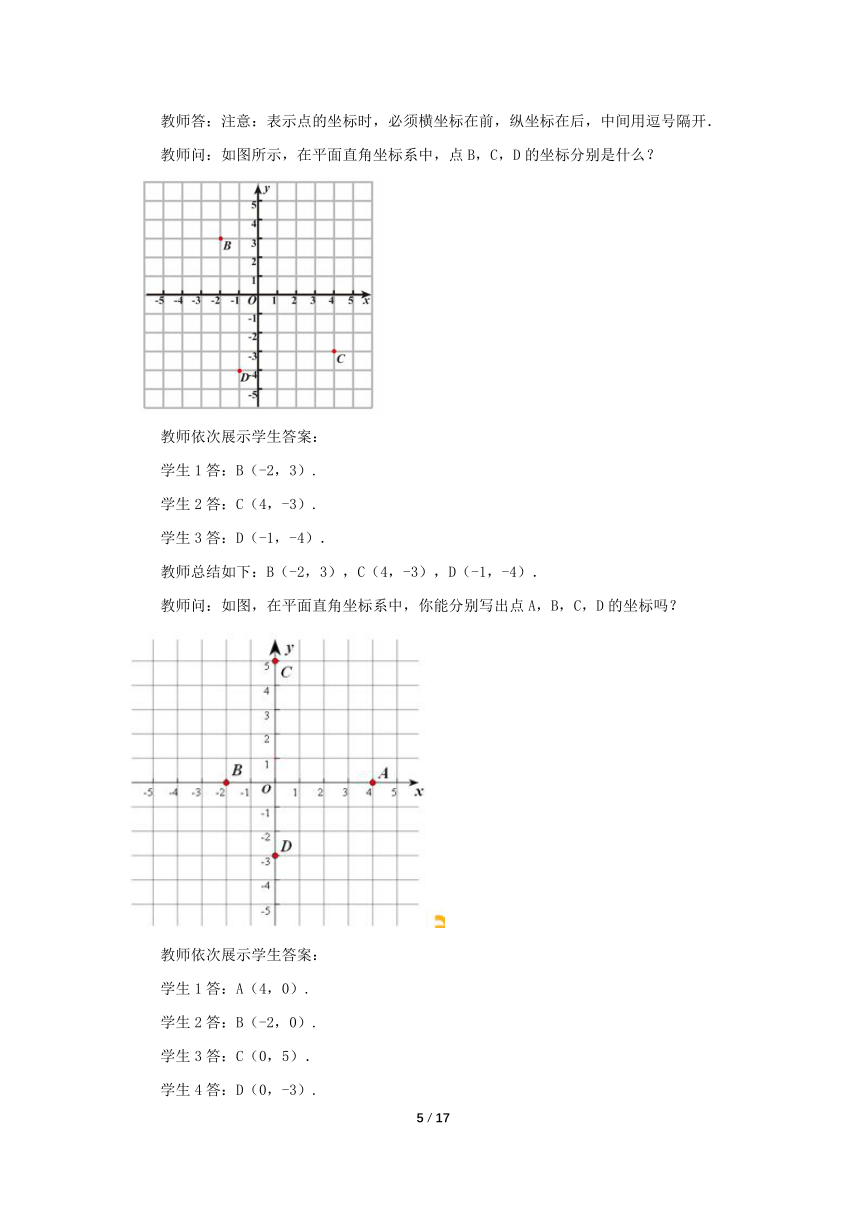
教师问:如图所示,在平面直角坐标系中,点B,C,D的坐标分别是什么?
教师依次展示学生答案:
学生1答:B(-2,3).
学生2答:C(4,-3).
学生3答:D(-1,-4).
教师总结如下:B(-2,3),C(4,-3),D(-1,-4).
教师问:如图,在平面直角坐标系中,你能分别写出点A,B,C,D的坐标吗?
教师依次展示学生答案:
学生1答:A(4,0).
学生2答:B(-2,0).
学生3答:C(0,5).
学生4答:D(0,-3).
教师总结如下:A(4,0),B(-2,0),C(0,5),D(0,-3).
教师问:观察上面点的坐标,你发现x轴和y轴上的点的坐标有什么特点?一般如何记录呢?
教师依次展示学生答案:
学生1答:x轴上的点的纵坐标为0,一般记为(x,0).
学生2答:y轴上的点的横坐标为0,一般记为(0,y).
教师总结如下:① x轴上的点的纵坐标为0,一般记为(x,0);
② y轴上的点的横坐标为0,一般记为(0,y);
教师问:观察上面点的平面直角坐标系,你发现原点的坐标有什么特点?一般如何记录呢?
学生答:原点O的坐标是(0,0).一般记为(0,0).
考点1:确定平面直角坐标系内点的坐标
写出下图中的多边形ABCDEF各个顶点的坐标.(出示课件15)
师生共同讨论后学生解答:
教师依次展示学生答案:
学生1答:A(-2,0).
学生2答:B(0,-3).
学生3答:C(3,-3).
学生4答:D(4,0).
学生5答:E(3,3).
学生6答:F(0,3).
教师总结如下:
解:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3)
出示课件16,学生自主练习后口答,教师订正.
3.出示课件17-20,探究平面直角坐标系内点的坐标性质
教师问:平面直角坐标系把平面分为了四部分,我们该如何正确识记每一部分呢?
学生思考后,师生一同作答:在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域. 分别称为第一,二,三,四象限.如下图所示.(出示课件17)
学生问:那么x轴和y轴上的点属于哪个象限呢?
教师答:坐标轴上的点不属于任何一个象限.
教师问:观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限
第四象限
教师依次展示学生答案:
学生1答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限 + +
第二象限
第三象限
第四象限
学生2答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限 - +
第三象限
第四象限
学生3答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限 - -
第四象限
学生4答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限
第四象限 + -
教师总结如下:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限 + +
第二象限 - +
第三象限 - -
第四象限 + -
教师问:不看平面直角坐标系,你能迅速说出A(4,5),B(-2,3),C(-4,-1)D(2.5,-2),E(0,-4)所在的象限吗?
教师依次展示学生答案:
学生1答:A(4,5)所在的象限是第一象限.
学生2答:B(-2,3)所在的象限是第二象限.
学生3答:C(-4,-1)所在的象限是第三象限.
学生4答:D(2.5,-2)所在的象限是第四象限.
学生5答:E(0,-4)在y轴上.
教师总结如下:A(4,5)所在的象限是第一象限;B(-2,3)所在的象限是第二象限;C(-4,-1)所在的象限是第三象限; D(2.5,-2)所在的象限是第四象限;E(0,-4)在y轴上.
教师问:你的方法又是什么?
学生答:根据点的坐标的符号确定点所在的象限.
教师问:观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
学生答:如下表所示:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上 + 0
在x轴的负半轴上 - 0
在y轴的正半轴上 0 +
在y轴的负半轴上 0 -
教师问:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?
教师依次展示学生答案:
学生1答:A(4,0)在x轴的正半轴.
学生2答:B(0,3)在y轴的正半轴.
学生3答:C(-4,0)在x轴的负半轴.
学生4答:E(0,-4)在y轴的负半轴.
学生5答:O(0,0)在原点.
教师总结如下:A(4,0)在x轴的正半轴; B(0,3)在y轴的正半轴;C(-4,0)在x轴的负半轴;E(0,-4)在y轴的负半轴;O(0,0)在原点.
教师问:你的确定点的方法又是什么?
学生答:根据点的坐标值和符号,在x轴上y的值为0,在y轴上x的值为0,在原点x、y的值都为0.
教师问:想一想:坐标平面内的点与有序数对(坐标)是什么关系
教师依次展示学生答案:
学生1答:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应.
学生2答:对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
教师总结如下:类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
考点2:在平面直角坐标系内确定已知点
在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),C (-4 ,-1),D(2,-4).(出示课件21)
学生独立思考后,师生共同解答.
解:如图,先在x 轴上找到表示5的点,再在y 轴上找出表示4 的点,过这两个点分别作x 轴,y 轴的垂线,垂线的交点就是点A. 类似地,其他各点的位置如图所示.点A 在第一象限,点B 在第二象限,点C在第三象限,点D在第四象限.
总结点拨:熟记各象限内点的坐标的符号特征:(+,+)表示第一象限内的点;(-,+)表示第二象限内的点;(-,-)表示第三象限内的点;(+,-)表示第四象限内的点.
出示课件22,学生自主练习后口答,教师订正.
考点3:利用平面直角坐标系内点的坐标确定字母的值
已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.(出示课件23)
师生共同分析:
根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组
解得m>2.
答案:m>2.
师生共同归纳:求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
出示课件24,学生自主练习,教师给出答案。
4.出示课件25-28,探究建立平面直角坐标系确定点的坐标
教师问:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
师生一起解答
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(0,0), B(4,0), C(4,4), D(0,4).
教师问:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
学生1答:(1)如图,以顶点D为原点,DC所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(0,-4), B(4,-4),C(4,0), D(0,0).
学生2答:(2)如图,以顶点B为原点,AB所在直线为x轴,BC所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-4,0), B(0,0),C(0,4), D(-4,4).
学生3答:(3)如图,以顶点C为原点,CD所在直线为x轴,BC所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-4,-4), B(0,-4),C(0,0), D(-4,0).
学生4答:(4)如图,以DC的垂直平分线和DA的垂直平分线的交点为原点,DC的垂直平分线为x轴,DA的垂直平分线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-2,-2), B(2,-2),C(2,2), D(-2,2).
教师问:由前面得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
师生一起解答:建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
考点4:建立平面直角坐标系确定点的坐标
长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.(出示课件29)
学生独立思考后,师生共同解答.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
出示课件30,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件31-37)
练习课件第31-37页题目,约用时20分钟.
(四)课堂小结(出示课件38)
平面直角坐标系 定义 原点、坐标轴
点的坐标 定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
(五)课前预习
预习下节课(7.2.1第1课时)的相关内容.
知道利用平面直角坐标系表示地理位置的方法.
课后作业
教材第68页练习第1,2题.
板书设计:
1.知识梳理
平面直角坐标系
2.考点讲解
考点1 考点2 考点3 考点4
教学反思:
成功之处:通过平面直角坐标系的有关内容的学习,反映平面直
角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生学习数学的积极性和好奇心.
不足之处:学生在自己建立平面直角坐标系时,容易忽视原点、x轴、y轴的标注,单位长的统一等,因此容易出错,这是需要加强的地方.
21 / 21
一、教学目标
【知识与技能】
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系 .
2.理解各象限内及坐标轴上点的坐标特征.
3.用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.
【过程与方法】
1.经历建立直角坐标系的过程,进而理解平面直角坐标系的意义.
2.通过分析具体特例得到特殊位置点的坐标特征以及有特殊位置关系的点的坐标的特征.
3.通过小组学习等活动经历建立坐标系的过程,进一步提高学生应用已有知识与技能的基础上形成新的知识,获得新的技能,以提高解决数学问题的能力.
【情感态度与价值观】
1.让学生体会到x轴、y轴的关系,进而明白事物之间是相互联系的这一辩证思想,培养耐心细致的良好学习作风.
2通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认同他人.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
平面直角坐标系的意义,由坐标找点,由点找坐标.
【教学难点】
平面直角坐标系内的点与有序数对一一对应的关系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
神舟九号、七号、六号和五号等卫星发射成功,圆了几代中国人的梦想,让全中国人为之骄傲和自豪!但是你们知道我们的科学家是怎样迅速地找到返回舱着陆的位置的吗?这就要依赖于GPS——卫星全球定位系统”.大家一定觉得很神奇吧!学习了今天的内容,你就会明白其中的奥妙.
(二)探索新知
1.出示课件4-9,探究平面直角坐标系的有关概念
教师问: 如何确定直线上点的位置?
学生答: 在直线上规定了原点、正方向、单位长度就构成了数轴.
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.
教师问:知道数轴上一点的坐标,能确定这个点的位置吗?
学生答:知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.例如在数轴上,坐标为2的点是B.
教师问:如何确定平面上点的位置?如下图:小强、小红、小明家的位置?
师生一起解答:利用两个数轴,使这两条数轴互相垂直,可以确定位置,如下图所示:
教师问:周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置. 小丽能根据小明的提示从左图中找出图书馆的位置吗?
学生答:小丽能根据小明的提示从左图中找出图书馆的位置.
教师问:小明是怎样描述图书馆的位置的?
学生答:利用方向和距离具体确定图书馆的位置.
教师问:小明可以省去“西边”和“北边”这几个字吗?
学生答:不能,省去“西边”和“北边”这几个字就不能准确找到图书馆了.
教师问:如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
学生答:不能找到.
教师问:如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
学生答:不能.
学生问:若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,能得到什么呢?
教师答:若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
总结点拨:(出示课件10)
出示课件11,学生自主练习后口答,教师订正.
2.出示课件12-14,探究确定平面直角坐标系内点的坐标
教师问:在平面直角坐标系中,能用有序数对来表示图中点A的位置吗?
学生答:由点A分别向 x轴,y轴作垂线,垂足M在 x轴上的坐标是3,垂足N在 y轴上的坐标是4,有序数对(3,4)就叫做点A的坐标,其中3是横坐标,4是纵坐标.
学生问:写有序数对要注意什么呢?
教师答:注意:表示点的坐标时,必须横坐标在前,纵坐标在后,中间用逗号隔开.
教师问:如图所示,在平面直角坐标系中,点B,C,D的坐标分别是什么?
教师依次展示学生答案:
学生1答:B(-2,3).
学生2答:C(4,-3).
学生3答:D(-1,-4).
教师总结如下:B(-2,3),C(4,-3),D(-1,-4).
教师问:如图,在平面直角坐标系中,你能分别写出点A,B,C,D的坐标吗?
教师依次展示学生答案:
学生1答:A(4,0).
学生2答:B(-2,0).
学生3答:C(0,5).
学生4答:D(0,-3).
教师总结如下:A(4,0),B(-2,0),C(0,5),D(0,-3).
教师问:观察上面点的坐标,你发现x轴和y轴上的点的坐标有什么特点?一般如何记录呢?
教师依次展示学生答案:
学生1答:x轴上的点的纵坐标为0,一般记为(x,0).
学生2答:y轴上的点的横坐标为0,一般记为(0,y).
教师总结如下:① x轴上的点的纵坐标为0,一般记为(x,0);
② y轴上的点的横坐标为0,一般记为(0,y);
教师问:观察上面点的平面直角坐标系,你发现原点的坐标有什么特点?一般如何记录呢?
学生答:原点O的坐标是(0,0).一般记为(0,0).
考点1:确定平面直角坐标系内点的坐标
写出下图中的多边形ABCDEF各个顶点的坐标.(出示课件15)
师生共同讨论后学生解答:
教师依次展示学生答案:
学生1答:A(-2,0).
学生2答:B(0,-3).
学生3答:C(3,-3).
学生4答:D(4,0).
学生5答:E(3,3).
学生6答:F(0,3).
教师总结如下:
解:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3)
出示课件16,学生自主练习后口答,教师订正.
3.出示课件17-20,探究平面直角坐标系内点的坐标性质
教师问:平面直角坐标系把平面分为了四部分,我们该如何正确识记每一部分呢?
学生思考后,师生一同作答:在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域. 分别称为第一,二,三,四象限.如下图所示.(出示课件17)
学生问:那么x轴和y轴上的点属于哪个象限呢?
教师答:坐标轴上的点不属于任何一个象限.
教师问:观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限
第四象限
教师依次展示学生答案:
学生1答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限 + +
第二象限
第三象限
第四象限
学生2答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限 - +
第三象限
第四象限
学生3答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限 - -
第四象限
学生4答:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限
第二象限
第三象限
第四象限 + -
教师总结如下:如下图所示:
点的位置 横坐标的符号 纵坐标 的符号
第一象限 + +
第二象限 - +
第三象限 - -
第四象限 + -
教师问:不看平面直角坐标系,你能迅速说出A(4,5),B(-2,3),C(-4,-1)D(2.5,-2),E(0,-4)所在的象限吗?
教师依次展示学生答案:
学生1答:A(4,5)所在的象限是第一象限.
学生2答:B(-2,3)所在的象限是第二象限.
学生3答:C(-4,-1)所在的象限是第三象限.
学生4答:D(2.5,-2)所在的象限是第四象限.
学生5答:E(0,-4)在y轴上.
教师总结如下:A(4,5)所在的象限是第一象限;B(-2,3)所在的象限是第二象限;C(-4,-1)所在的象限是第三象限; D(2.5,-2)所在的象限是第四象限;E(0,-4)在y轴上.
教师问:你的方法又是什么?
学生答:根据点的坐标的符号确定点所在的象限.
教师问:观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
学生答:如下表所示:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上 + 0
在x轴的负半轴上 - 0
在y轴的正半轴上 0 +
在y轴的负半轴上 0 -
教师问:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?
教师依次展示学生答案:
学生1答:A(4,0)在x轴的正半轴.
学生2答:B(0,3)在y轴的正半轴.
学生3答:C(-4,0)在x轴的负半轴.
学生4答:E(0,-4)在y轴的负半轴.
学生5答:O(0,0)在原点.
教师总结如下:A(4,0)在x轴的正半轴; B(0,3)在y轴的正半轴;C(-4,0)在x轴的负半轴;E(0,-4)在y轴的负半轴;O(0,0)在原点.
教师问:你的确定点的方法又是什么?
学生答:根据点的坐标值和符号,在x轴上y的值为0,在y轴上x的值为0,在原点x、y的值都为0.
教师问:想一想:坐标平面内的点与有序数对(坐标)是什么关系
教师依次展示学生答案:
学生1答:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应.
学生2答:对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
教师总结如下:类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
考点2:在平面直角坐标系内确定已知点
在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),C (-4 ,-1),D(2,-4).(出示课件21)
学生独立思考后,师生共同解答.
解:如图,先在x 轴上找到表示5的点,再在y 轴上找出表示4 的点,过这两个点分别作x 轴,y 轴的垂线,垂线的交点就是点A. 类似地,其他各点的位置如图所示.点A 在第一象限,点B 在第二象限,点C在第三象限,点D在第四象限.
总结点拨:熟记各象限内点的坐标的符号特征:(+,+)表示第一象限内的点;(-,+)表示第二象限内的点;(-,-)表示第三象限内的点;(+,-)表示第四象限内的点.
出示课件22,学生自主练习后口答,教师订正.
考点3:利用平面直角坐标系内点的坐标确定字母的值
已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.(出示课件23)
师生共同分析:
根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组
解得m>2.
答案:m>2.
师生共同归纳:求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
出示课件24,学生自主练习,教师给出答案。
4.出示课件25-28,探究建立平面直角坐标系确定点的坐标
教师问:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
师生一起解答
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(0,0), B(4,0), C(4,4), D(0,4).
教师问:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
学生1答:(1)如图,以顶点D为原点,DC所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(0,-4), B(4,-4),C(4,0), D(0,0).
学生2答:(2)如图,以顶点B为原点,AB所在直线为x轴,BC所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-4,0), B(0,0),C(0,4), D(-4,4).
学生3答:(3)如图,以顶点C为原点,CD所在直线为x轴,BC所在直线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-4,-4), B(0,-4),C(0,0), D(-4,0).
学生4答:(4)如图,以DC的垂直平分线和DA的垂直平分线的交点为原点,DC的垂直平分线为x轴,DA的垂直平分线为y轴建立平面直角坐标系.此时,正方形四个顶点A,B,C,D的坐标分别为:A(-2,-2), B(2,-2),C(2,2), D(-2,2).
教师问:由前面得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
师生一起解答:建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
考点4:建立平面直角坐标系确定点的坐标
长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.(出示课件29)
学生独立思考后,师生共同解答.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
出示课件30,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件31-37)
练习课件第31-37页题目,约用时20分钟.
(四)课堂小结(出示课件38)
平面直角坐标系 定义 原点、坐标轴
点的坐标 定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
(五)课前预习
预习下节课(7.2.1第1课时)的相关内容.
知道利用平面直角坐标系表示地理位置的方法.
课后作业
教材第68页练习第1,2题.
板书设计:
1.知识梳理
平面直角坐标系
2.考点讲解
考点1 考点2 考点3 考点4
教学反思:
成功之处:通过平面直角坐标系的有关内容的学习,反映平面直
角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生学习数学的积极性和好奇心.
不足之处:学生在自己建立平面直角坐标系时,容易忽视原点、x轴、y轴的标注,单位长的统一等,因此容易出错,这是需要加强的地方.
21 / 21
