人教版七年级数学下册 8.3 实际问题与二元一次方程组(第2课时)教案
文档属性
| 名称 | 人教版七年级数学下册 8.3 实际问题与二元一次方程组(第2课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:40:50 | ||
图片预览


文档简介
8.3 实际问题与二元一次方程组
第2课时
一、教学目标
【知识与技能】
1.学会运用二元一次方程组解决较复杂的实际问题 .
2.进一步经历和体验方程组解决实际问题的过程,提高运用方程组解决问题的能力.
【过程与方法】
学生已经会初步分析问题中所蕴涵的数量关系,列出二元一次方程组解决实际问题,这节课主要通过自主探究和合作讨论让学生进一步熟练解题过程和方法.
【情感态度与价值观】
培养分析问题、解决问题的能力,进一步体会二元一次方程组的应用价值.
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
用列表的方式分析题目中的各个量的关系.
【教学难点】
借助列表分问题中所蕴含的数量关系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
1.把长方形纸片折成面积相等的两个小长方形,有哪些折法?
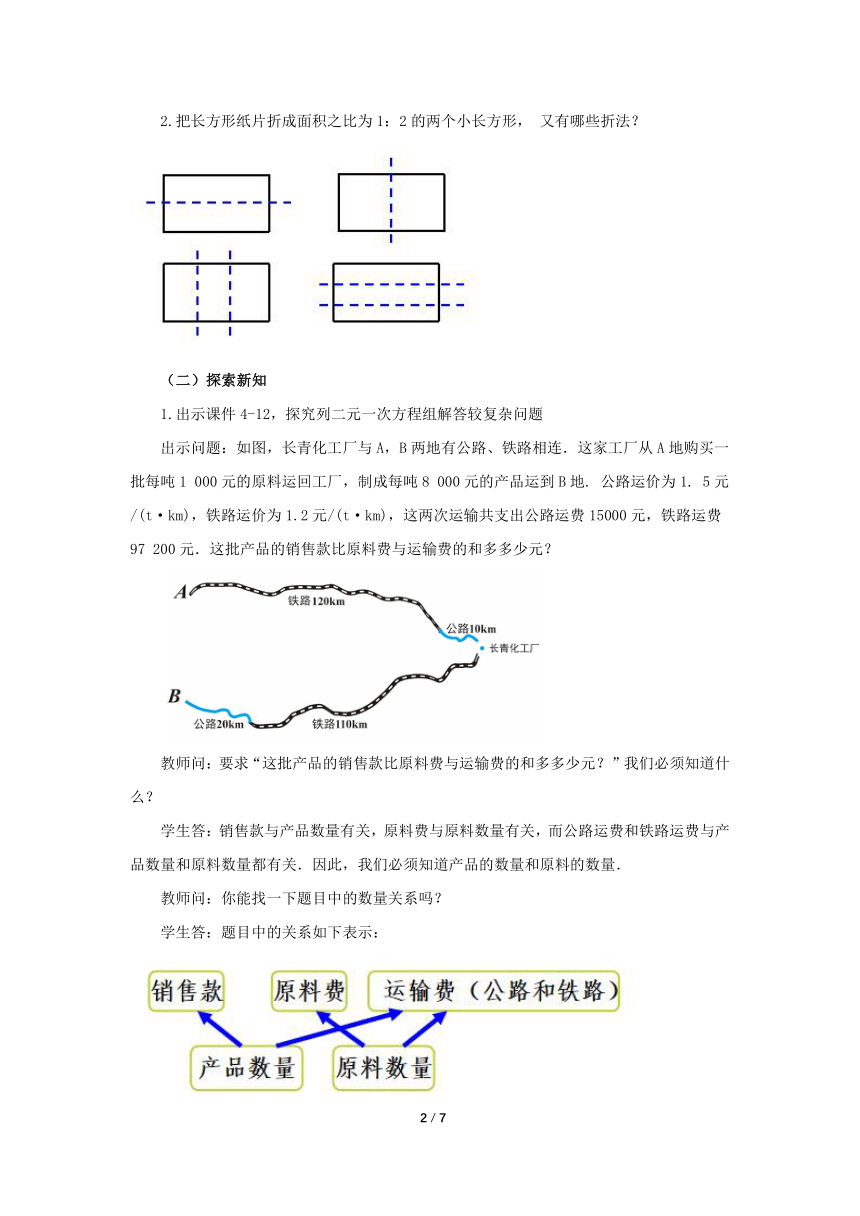
2.把长方形纸片折成面积之比为1:2的两个小长方形, 又有哪些折法?
(二)探索新知
1.出示课件4-12,探究列二元一次方程组解答较复杂问题
出示问题:如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
教师问:要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
学生答:销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
教师问:你能找一下题目中的数量关系吗?
学生答:题目中的关系如下表示:
教师问:本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
学生1答:一类是公路运费,铁路运费,价值;
学生2答:另一类是产品数量,原料数量.
教师问:你能完成下面的表格吗?
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y
铁路运费(元) 1.2×110x 1.2×120y
价值(元) 8 000x 1 000y
学生答:填写表格如下:
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y 1.5(20x+10y)
铁路运费(元) 1.2×110x 1.2×120y 1.2(110x+120y)
价值(元) 8 000x 1 000y
教师问:观察上表,你发现等量关系了吗?如何列方程组并求解?
师生一起解答:
解:先化简,得
由①,得y=1000-2x,③
代入② ,得11x+12(1000-2x)=8100,
解得x=300.
代入③ ,得y=400.
∴是原方程组的解.
教师问:这个实际问题的答案是什么?
学生答:销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2400000-400000-112200=1887800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
教师问:在什么情况下考虑选择设间接未知数?
学生答:当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
教师问:如何更好地分析数量关系比较复杂的实际问题?
师生一起解答:
出示课件13-14,学生自主练习后口答,教师订正.
考点1:列二元一次方程组解答利润问题
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题 (出示课件15)
师生共同讨论解答如下:(出示课件16)
学生1解:解法一:方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000 (元)
其余5吨直接销售,获利500×5=2500(元),
∴共获利:8000+2500=10500(元).
方案二:设生产奶片用x天,生产酸奶用y天
根据题意,得方程组
解得
∴共获利: 1.5×1×2000+2.5×3×1200=12000 (元).
学生2解:解法二:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶,
根据题意,得方程组
解得
∴共获利: 1.5×2000+7.5×1200=3000+9000=12000 (元).
出示课件17,学生自主练习后口答,教师订正.
考点2:列二元一次方程组解答配套问题
某车间每天能生产甲种零件600个或乙种零件300个,或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
学生独立思考后,师生共同解答.
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
解得
所以63-x-y=18.
答:甲、乙、丙三种零件各应生产15天、30天和18天.
出示课件20,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件22-30)
练习课件第22-30页题目,约用时20分钟.
(四)课堂小结(出示课件31)
通过本课时的学习,需要我们掌握:
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
利用方程组解决较复杂的实际问题.
(五)课前预习
预习下节课(8.4第1课时)的相关内容.
知道三元一次方程、三元一次方程组的定义及会解三元一次方程组.
课后作业
教材第101页习题8.4第2,3题.
板书设计:
8.3实际问题与二元一次方程复习课二
1.考点讲解
考点1 考点2
2.练习与作业.
九、教学反思:
成功之处:通过问题的解决使学生进一步认识数学与现实世界的密切联系,乐于接触生活环境中的数学信息,愿意参与数学话题的研讨,从中懂得数学的价值,逐步形成运用数学的意识.并且通过对问题的解决,培养学生合理优化的经济意识,增强他们节约和有效合理利用资源的意识.
不足之处:当题目中数量关系比较多,情况比较复杂时,通过列表格找关系直观明了,容易理解,但是学生往往不会画出表格,需要老师细心讲解,耐心指导,因为在课上练习讲解不够,所以课后还需要加强.
8 / 9
第2课时
一、教学目标
【知识与技能】
1.学会运用二元一次方程组解决较复杂的实际问题 .
2.进一步经历和体验方程组解决实际问题的过程,提高运用方程组解决问题的能力.
【过程与方法】
学生已经会初步分析问题中所蕴涵的数量关系,列出二元一次方程组解决实际问题,这节课主要通过自主探究和合作讨论让学生进一步熟练解题过程和方法.
【情感态度与价值观】
培养分析问题、解决问题的能力,进一步体会二元一次方程组的应用价值.
二、课型
新授课
三、课时
第2课时 共2课时
四、教学重难点
【教学重点】
用列表的方式分析题目中的各个量的关系.
【教学难点】
借助列表分问题中所蕴含的数量关系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本.
六、教学过程
(一)导入新课(出示课件2)
1.把长方形纸片折成面积相等的两个小长方形,有哪些折法?
2.把长方形纸片折成面积之比为1:2的两个小长方形, 又有哪些折法?
(二)探索新知
1.出示课件4-12,探究列二元一次方程组解答较复杂问题
出示问题:如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
教师问:要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
学生答:销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
教师问:你能找一下题目中的数量关系吗?
学生答:题目中的关系如下表示:
教师问:本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
学生1答:一类是公路运费,铁路运费,价值;
学生2答:另一类是产品数量,原料数量.
教师问:你能完成下面的表格吗?
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y
铁路运费(元) 1.2×110x 1.2×120y
价值(元) 8 000x 1 000y
学生答:填写表格如下:
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y 1.5(20x+10y)
铁路运费(元) 1.2×110x 1.2×120y 1.2(110x+120y)
价值(元) 8 000x 1 000y
教师问:观察上表,你发现等量关系了吗?如何列方程组并求解?
师生一起解答:
解:先化简,得
由①,得y=1000-2x,③
代入② ,得11x+12(1000-2x)=8100,
解得x=300.
代入③ ,得y=400.
∴是原方程组的解.
教师问:这个实际问题的答案是什么?
学生答:销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2400000-400000-112200=1887800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
教师问:在什么情况下考虑选择设间接未知数?
学生答:当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
教师问:如何更好地分析数量关系比较复杂的实际问题?
师生一起解答:
出示课件13-14,学生自主练习后口答,教师订正.
考点1:列二元一次方程组解答利润问题
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题 (出示课件15)
师生共同讨论解答如下:(出示课件16)
学生1解:解法一:方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000 (元)
其余5吨直接销售,获利500×5=2500(元),
∴共获利:8000+2500=10500(元).
方案二:设生产奶片用x天,生产酸奶用y天
根据题意,得方程组
解得
∴共获利: 1.5×1×2000+2.5×3×1200=12000 (元).
学生2解:解法二:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶,
根据题意,得方程组
解得
∴共获利: 1.5×2000+7.5×1200=3000+9000=12000 (元).
出示课件17,学生自主练习后口答,教师订正.
考点2:列二元一次方程组解答配套问题
某车间每天能生产甲种零件600个或乙种零件300个,或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
学生独立思考后,师生共同解答.
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
解得
所以63-x-y=18.
答:甲、乙、丙三种零件各应生产15天、30天和18天.
出示课件20,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件22-30)
练习课件第22-30页题目,约用时20分钟.
(四)课堂小结(出示课件31)
通过本课时的学习,需要我们掌握:
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
利用方程组解决较复杂的实际问题.
(五)课前预习
预习下节课(8.4第1课时)的相关内容.
知道三元一次方程、三元一次方程组的定义及会解三元一次方程组.
课后作业
教材第101页习题8.4第2,3题.
板书设计:
8.3实际问题与二元一次方程复习课二
1.考点讲解
考点1 考点2
2.练习与作业.
九、教学反思:
成功之处:通过问题的解决使学生进一步认识数学与现实世界的密切联系,乐于接触生活环境中的数学信息,愿意参与数学话题的研讨,从中懂得数学的价值,逐步形成运用数学的意识.并且通过对问题的解决,培养学生合理优化的经济意识,增强他们节约和有效合理利用资源的意识.
不足之处:当题目中数量关系比较多,情况比较复杂时,通过列表格找关系直观明了,容易理解,但是学生往往不会画出表格,需要老师细心讲解,耐心指导,因为在课上练习讲解不够,所以课后还需要加强.
8 / 9
