人教版八年级数学下册17.1 勾股定理(第1课时)教案
文档属性
| 名称 | 人教版八年级数学下册17.1 勾股定理(第1课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 273.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:48:54 | ||
图片预览


文档简介
17.1 勾股定理
第1课时
一、教学目标
【知识与技能】
1.了解勾股定理的文化背景,了解利用拼图验证勾股定理的方法.
2.能说出勾股定理,并能应用其进行简单的计算.
【过程与方法】
1.在勾股定理的探索过程中,经历观察——猜想——归纳——验证的数学发现过程.
2.发展合情推理的能力,体会数形结合思想、由特殊到一般的数学思想、分类讨论思想.
【情感态度与价值观】
通过对勾股定理历史的了解和实例应用,体会勾股定理的文化价值;通过获得成功的经验和克服困难的经历,增强学习数学的信心,激发学生的民族自豪感和爱国情怀.
二、课型
新授课
三、课时
第1课时 共3课时
四、教学重难点
【教学重点】
探索和验证勾股定理,并能应用其进行简单的计算.
【教学难点】
用拼图的方法验证勾股定理.
五、课前准备
教师:课件、三角尺、直尺、方格纸、三角模型等.
学生:三角尺、铅笔、练习本、方格纸、三角模型.
六、教学过程
(一)导入新课(出示课件2)
引导学生观察勾股定理相关图片,引出本节要学知识
(二)探索新知
1.出示课件4-10,探究勾股定理的认识与证明
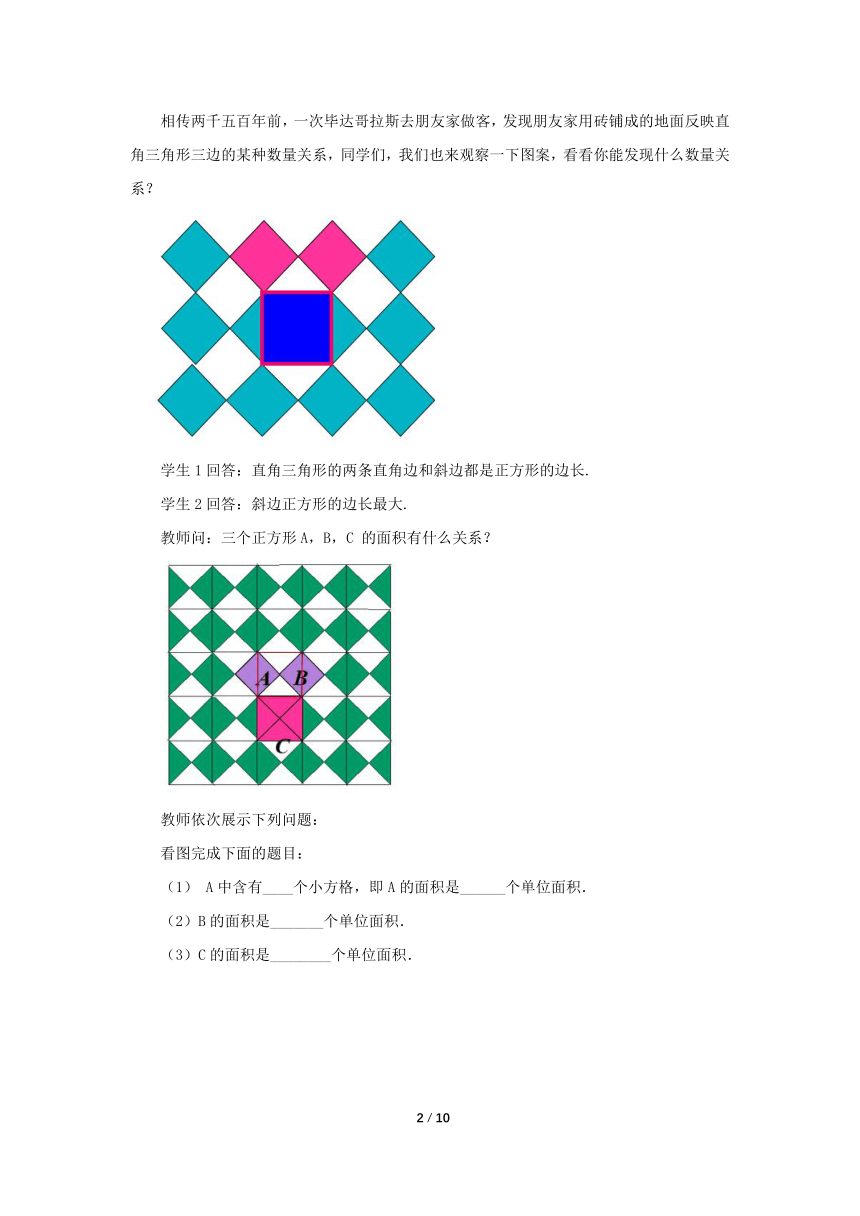
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察一下图案,看看你能发现什么数量关系?
学生1回答:直角三角形的两条直角边和斜边都是正方形的边长.
学生2回答:斜边正方形的边长最大.
教师问:三个正方形A,B,C 的面积有什么关系?
教师依次展示下列问题:
看图完成下面的题目:
(1) A中含有____个小方格,即A的面积是______个单位面积.
(2)B的面积是_______个单位面积.
(3)C的面积是________个单位面积.
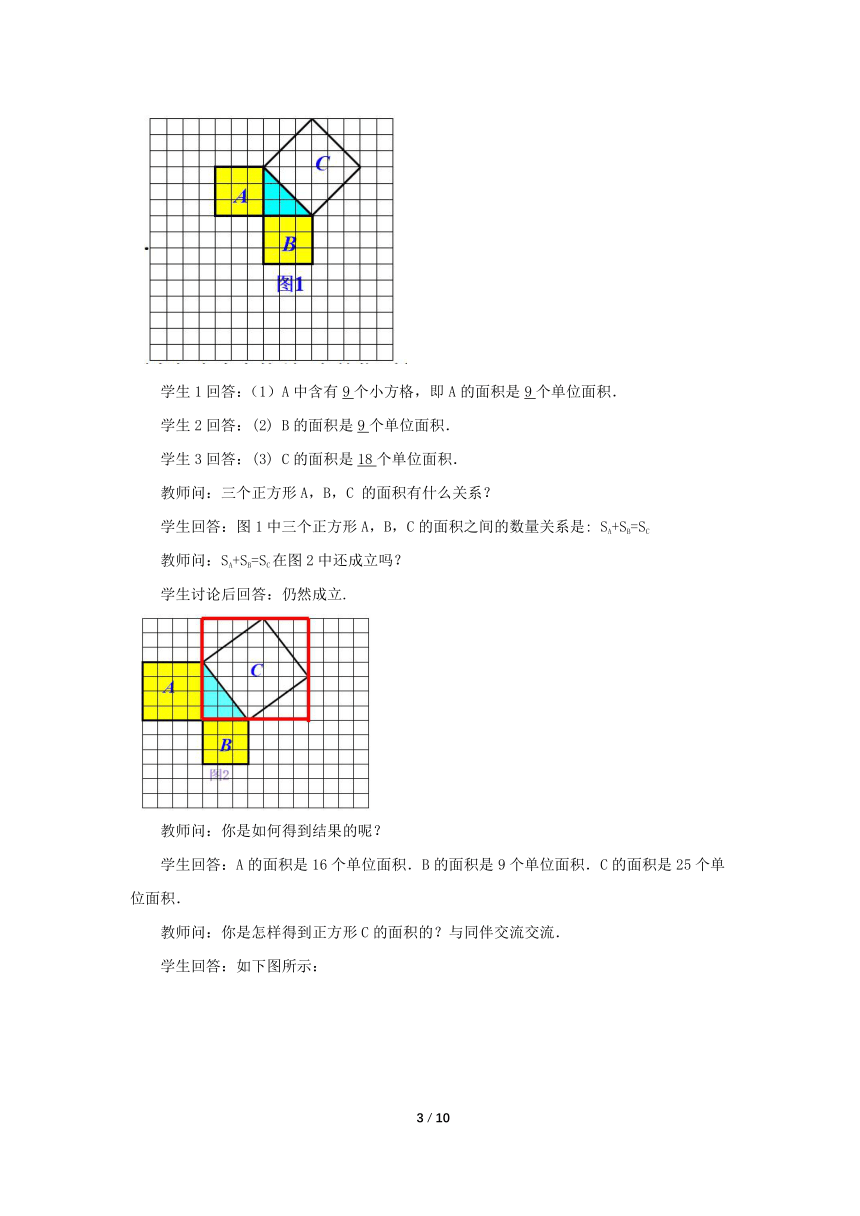
学生1回答:(1)A中含有9个小方格,即A的面积是9个单位面积.
学生2回答:(2) B的面积是9个单位面积.
学生3回答:(3) C的面积是18个单位面积.
教师问:三个正方形A,B,C 的面积有什么关系?
学生回答:图1中三个正方形A,B,C的面积之间的数量关系是: SA+SB=SC
教师问:SA+SB=SC在图2中还成立吗?
学生讨论后回答:仍然成立.
教师问:你是如何得到结果的呢?
学生回答:A的面积是16个单位面积.B的面积是9个单位面积.C的面积是25个单位面积.
教师问:你是怎样得到正方形C的面积的?与同伴交流交流.
学生回答:如下图所示:
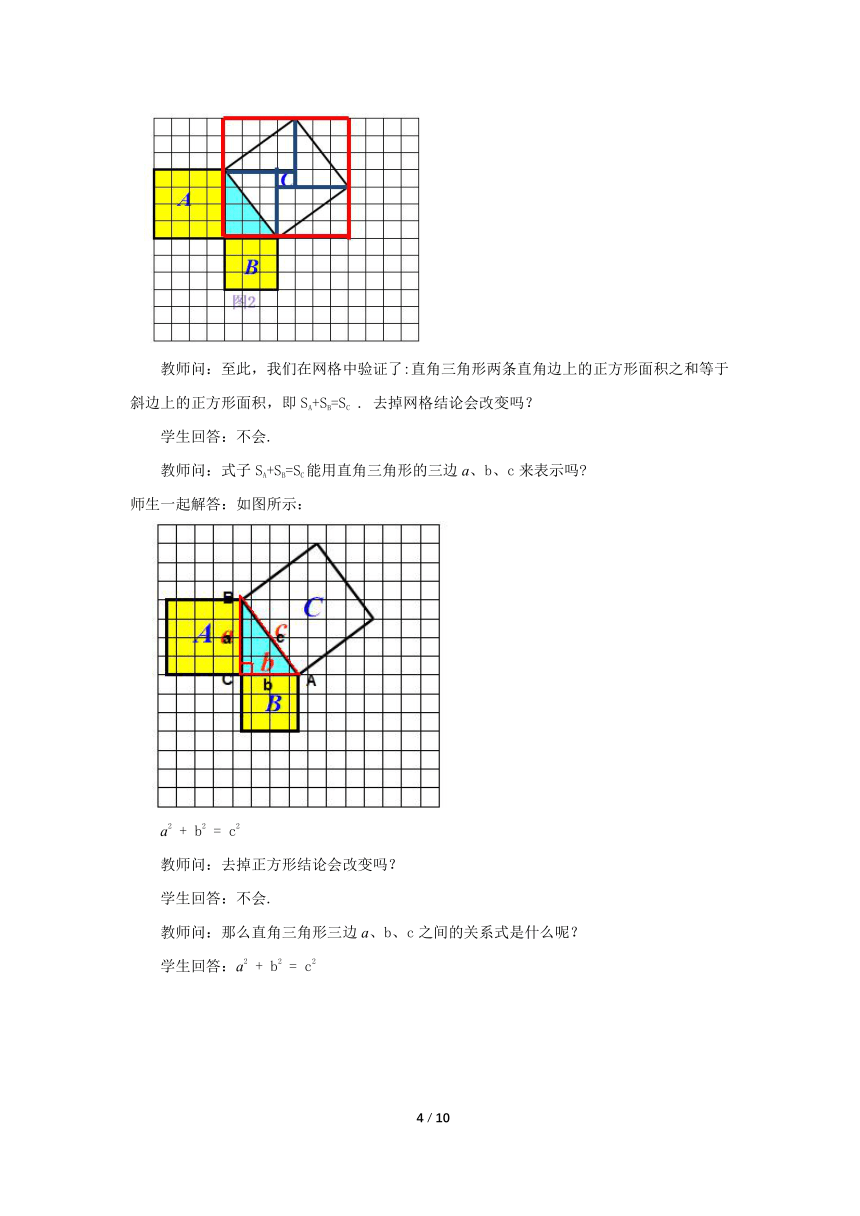
教师问:至此,我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC . 去掉网格结论会改变吗?
学生回答:不会.
教师问:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
师生一起解答:如图所示:
a2 + b2 = c2
教师问:去掉正方形结论会改变吗?
学生回答:不会.
教师问:那么直角三角形三边a、b、c之间的关系式是什么呢?
学生回答:a2 + b2 = c2
教师:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
如何利用拼图证明呢?
师生一起看数学家的证明:
是不是所有的直角三角形都具有这样的结论呢?光靠实验和猜想还不能把问题彻底搞清楚.
这就需要我们对一般的直角三角形进行证明.下面我们就一起来探究,看一看我国古代数学家赵爽是怎样证明这个命题的.
教师依次展示各种证明方法:
(1)赵爽拼图证明法:
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
小组活动:仿照课本中赵爽的思路,只剪两刀,将两个连体正方形,拼成一个新的正方形.
剪、拼过程展示:(出示课件11)
教师问:如何进行证明呢?
师生共同讨论后解答如下:
证明:∵S大正方形=c2,S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
∴c2=4×+(b-a)2=a2+b2
(2) 毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.(出示课件13)
教师问:观看拼图过程演示后,你能证明吗?
师生共同讨论后解答如下:
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+S小正方形
=4×ab+c2
=c2+2ab,
∴a2+b2+2ab=c2+2ab,
∴a2+b2=c2.
(3)美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
教师问:你能证明上边的问题吗?
学生讨论后回答:
证明:
∵S梯形=(a+b)(a+b),
S梯形=ab+ab+c2,
∴a2 + b2 = c2.
教师总结归纳;(出示课件16)
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么a2 + b2 = c2.
即直角三角形两直角边的平方和等于斜边的平方.
表示为:Rt△ABC中,∠C=90°, 则a2 + b2 = c2.
总结点拨:(出示课件17)
公式变形
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方.
出示课件18,学生口答,教师订正。
考点1:利用勾股定理求直角三角形的边长
如图,在Rt△ABC中,∠C=90°.(出示课件19)
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
师生共同讨论解答如下:
解:(1)据勾股定理得
(2)据勾股定理得
出示课件20,学生自主练习后口答,教师订正.
考点2:勾股定理和方程相结合求直角三角形的边长
在Rt△ABC中, ∠C=90°.(出示课件21)
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
学生独立思考后,师生共同解答.
解:(1)设a=x,b=2x,根据勾股定理建立方程得x2+(2x)2=52,
解得 (舍去)
(2)
因此设a=x,c=2x,根据勾股定理建立方程得(2x)2-x2=152,
解得 (舍去)
总结点拨:(出示课件21)
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
出示课件22,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件23-27)
练习课件第23-27页题目,约用时20分钟.
(四)课堂小结(出示课件28)
内 容
勾股定理 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
注 意 1.在直角三角形中 2.看清哪个角是直角 3.已知两边没有指明是直角边还是斜边时一定要分类讨论
(五)课前预习
预习下节课(17.1第2课时)的相关内容.
会用勾股定理解决实际问题.
七、课后作业
教材第24页练习第1,2题.
八、板书设计
勾股定理 第1课时
1.探索勾股定理
2.勾股定理的证明
考点1 考点2
3.例题讲解
九、教学反思
成功之处:本节课从知识与方法、能力与素质的层面确定了相应的教学目标.把学生的探索和验证活动放在首位,一方面要求学生在老师的引导下自主探索,合作交流,另一方面要求学生对探究过程中用到的数学思想方法有一定的领悟和认识,达到培养能力的目的.整节课以“问题情境——分析探究——得出猜想——实践验证——总结升华”为主线,使学生亲身体验勾股定理的探索和验证过程,努力做到由传统的数学课堂向实验课堂转变.
不足之处:在教学过程中,高估了学生证明勾股定理的能力,主要困难在于一些学生不能对图形进行正确的割补.对图形的割补过程没有给学生详细的呈现.
补救措施:适当增加学生拼图的时间,通过实践操作,画图分析,独立分析证明思路,正确完成证明过程.
12 / 13
第1课时
一、教学目标
【知识与技能】
1.了解勾股定理的文化背景,了解利用拼图验证勾股定理的方法.
2.能说出勾股定理,并能应用其进行简单的计算.
【过程与方法】
1.在勾股定理的探索过程中,经历观察——猜想——归纳——验证的数学发现过程.
2.发展合情推理的能力,体会数形结合思想、由特殊到一般的数学思想、分类讨论思想.
【情感态度与价值观】
通过对勾股定理历史的了解和实例应用,体会勾股定理的文化价值;通过获得成功的经验和克服困难的经历,增强学习数学的信心,激发学生的民族自豪感和爱国情怀.
二、课型
新授课
三、课时
第1课时 共3课时
四、教学重难点
【教学重点】
探索和验证勾股定理,并能应用其进行简单的计算.
【教学难点】
用拼图的方法验证勾股定理.
五、课前准备
教师:课件、三角尺、直尺、方格纸、三角模型等.
学生:三角尺、铅笔、练习本、方格纸、三角模型.
六、教学过程
(一)导入新课(出示课件2)
引导学生观察勾股定理相关图片,引出本节要学知识
(二)探索新知
1.出示课件4-10,探究勾股定理的认识与证明
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察一下图案,看看你能发现什么数量关系?
学生1回答:直角三角形的两条直角边和斜边都是正方形的边长.
学生2回答:斜边正方形的边长最大.
教师问:三个正方形A,B,C 的面积有什么关系?
教师依次展示下列问题:
看图完成下面的题目:
(1) A中含有____个小方格,即A的面积是______个单位面积.
(2)B的面积是_______个单位面积.
(3)C的面积是________个单位面积.
学生1回答:(1)A中含有9个小方格,即A的面积是9个单位面积.
学生2回答:(2) B的面积是9个单位面积.
学生3回答:(3) C的面积是18个单位面积.
教师问:三个正方形A,B,C 的面积有什么关系?
学生回答:图1中三个正方形A,B,C的面积之间的数量关系是: SA+SB=SC
教师问:SA+SB=SC在图2中还成立吗?
学生讨论后回答:仍然成立.
教师问:你是如何得到结果的呢?
学生回答:A的面积是16个单位面积.B的面积是9个单位面积.C的面积是25个单位面积.
教师问:你是怎样得到正方形C的面积的?与同伴交流交流.
学生回答:如下图所示:
教师问:至此,我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC . 去掉网格结论会改变吗?
学生回答:不会.
教师问:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
师生一起解答:如图所示:
a2 + b2 = c2
教师问:去掉正方形结论会改变吗?
学生回答:不会.
教师问:那么直角三角形三边a、b、c之间的关系式是什么呢?
学生回答:a2 + b2 = c2
教师:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
如何利用拼图证明呢?
师生一起看数学家的证明:
是不是所有的直角三角形都具有这样的结论呢?光靠实验和猜想还不能把问题彻底搞清楚.
这就需要我们对一般的直角三角形进行证明.下面我们就一起来探究,看一看我国古代数学家赵爽是怎样证明这个命题的.
教师依次展示各种证明方法:
(1)赵爽拼图证明法:
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
小组活动:仿照课本中赵爽的思路,只剪两刀,将两个连体正方形,拼成一个新的正方形.
剪、拼过程展示:(出示课件11)
教师问:如何进行证明呢?
师生共同讨论后解答如下:
证明:∵S大正方形=c2,S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
∴c2=4×+(b-a)2=a2+b2
(2) 毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.(出示课件13)
教师问:观看拼图过程演示后,你能证明吗?
师生共同讨论后解答如下:
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+S小正方形
=4×ab+c2
=c2+2ab,
∴a2+b2+2ab=c2+2ab,
∴a2+b2=c2.
(3)美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
教师问:你能证明上边的问题吗?
学生讨论后回答:
证明:
∵S梯形=(a+b)(a+b),
S梯形=ab+ab+c2,
∴a2 + b2 = c2.
教师总结归纳;(出示课件16)
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么a2 + b2 = c2.
即直角三角形两直角边的平方和等于斜边的平方.
表示为:Rt△ABC中,∠C=90°, 则a2 + b2 = c2.
总结点拨:(出示课件17)
公式变形
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方.
出示课件18,学生口答,教师订正。
考点1:利用勾股定理求直角三角形的边长
如图,在Rt△ABC中,∠C=90°.(出示课件19)
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
师生共同讨论解答如下:
解:(1)据勾股定理得
(2)据勾股定理得
出示课件20,学生自主练习后口答,教师订正.
考点2:勾股定理和方程相结合求直角三角形的边长
在Rt△ABC中, ∠C=90°.(出示课件21)
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
学生独立思考后,师生共同解答.
解:(1)设a=x,b=2x,根据勾股定理建立方程得x2+(2x)2=52,
解得 (舍去)
(2)
因此设a=x,c=2x,根据勾股定理建立方程得(2x)2-x2=152,
解得 (舍去)
总结点拨:(出示课件21)
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
出示课件22,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件23-27)
练习课件第23-27页题目,约用时20分钟.
(四)课堂小结(出示课件28)
内 容
勾股定理 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
注 意 1.在直角三角形中 2.看清哪个角是直角 3.已知两边没有指明是直角边还是斜边时一定要分类讨论
(五)课前预习
预习下节课(17.1第2课时)的相关内容.
会用勾股定理解决实际问题.
七、课后作业
教材第24页练习第1,2题.
八、板书设计
勾股定理 第1课时
1.探索勾股定理
2.勾股定理的证明
考点1 考点2
3.例题讲解
九、教学反思
成功之处:本节课从知识与方法、能力与素质的层面确定了相应的教学目标.把学生的探索和验证活动放在首位,一方面要求学生在老师的引导下自主探索,合作交流,另一方面要求学生对探究过程中用到的数学思想方法有一定的领悟和认识,达到培养能力的目的.整节课以“问题情境——分析探究——得出猜想——实践验证——总结升华”为主线,使学生亲身体验勾股定理的探索和验证过程,努力做到由传统的数学课堂向实验课堂转变.
不足之处:在教学过程中,高估了学生证明勾股定理的能力,主要困难在于一些学生不能对图形进行正确的割补.对图形的割补过程没有给学生详细的呈现.
补救措施:适当增加学生拼图的时间,通过实践操作,画图分析,独立分析证明思路,正确完成证明过程.
12 / 13
