人教版八年级数学下册17.1 勾股定理(第2课时)教案
文档属性
| 名称 | 人教版八年级数学下册17.1 勾股定理(第2课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 73.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:49:14 | ||
图片预览

文档简介
17.1 勾股定理
第2课时
一、教学目标
【知识与技能】
1.能应用勾股定理计算直角三角形的边长.
2.能应用勾股定理解决简单的实际问题.
3.能说出勾股定理,能运用勾股定理的数学模型解决现实世界的实际问题.
【过程与方法】
1.通过从实际问题中抽象出直角三角形这一模型,强化转化思想,培养学生解决现实问题的意识和能力.
2.经历探究勾股定理在实际问题中的应用过程,进一步体会勾股定理的应用方法.
【情感态度与价值观】
在例题分析和解决过程中,让学生感受勾股定理在实际生活中的应用.同时在学习过程中体会获得成功的喜悦,提高学生学习数学的兴趣和信心.
二、课型
新授课
三、课时
第2课时 共3课时
四、教学重难点
【教学重点】
运用勾股定理解决实际问题.
【教学难点】
勾股定理的灵活运用.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、直尺、练习本、三角形模型.
六、教学过程
(一)导入新课(出示课件2)
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.
离开原处6尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺?
示意图见课件,就是求AD的长
教师:这节课我们就来学习用勾股定理解决实际问题,学完本节课知识后,自己再想想怎么计算此题吧!
(二)探索新知
1.出示课件4-6,探究勾股定理解决线段长度问题
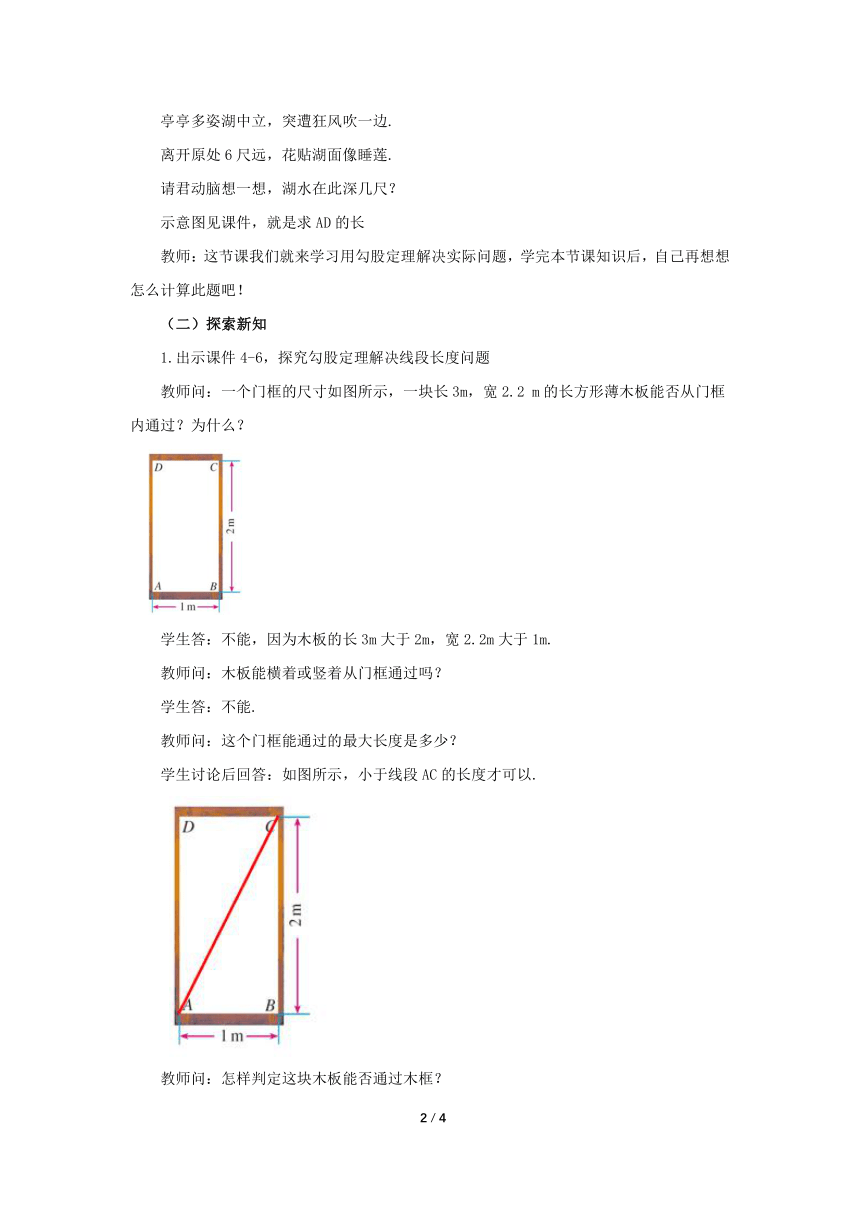
教师问:一个门框的尺寸如图所示,一块长3m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
学生答:不能,因为木板的长3m大于2m,宽2.2m大于1m.
教师问:木板能横着或竖着从门框通过吗?
学生答:不能.
教师问:这个门框能通过的最大长度是多少?
学生讨论后回答:如图所示,小于线段AC的长度才可以.
教师问:怎样判定这块木板能否通过木框?
学生回答:求出斜边AC的长,与木板的宽比较.
师生一起解答:
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所以木板能从门框内通过.
出示课件7,学生自主练习后口答,教师订正.
2.出示课件8-9,探究勾股定理解决线段移动问题
教师问:如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.求梯子的底端B距墙角O多少米?
学生回答:
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
教师问:如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
学生回答:在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
OD=≈1.77.BD=OD-OB≈1.77-1=0.77
答:梯子底端B也外移约0.77米.
出示课件10,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件12-19)
练习课件第12-19页题目,约用时20分钟.
(四)课堂小结(出示课件20)
用勾股定理计算时,要先画好图形,并标好图形,理清各边之间的关系,再灵活运用勾股定理计算.在利用勾股定理进行有关计算和证明时,要注意运用方程的思想;求直角三角形有关线段的长,有时还要运用转化的数学思想,或利用添加辅助线的方法构造直角三角形,再运用勾股定理求解.
(五)课前预习
预习下节课(17.1第3课时)的相关内容.
知道如何在数轴上标出无理数及构造直角三角形表示出无理数.
七、课后作业
教材第26页练习第1,2题.
八、板书设计
勾股定理 第2课时
1.解决线段长度问题
2.解决线段移动问题
3.例题讲解
九、教学反思
成功之处:本节课运用勾股定理解决实际问题,整节课注重基础,通过分类探索,由浅入深,注重讲练结合,引导学生独立分析,自主学习,提高学生运用勾股定理解决简单问题的能力.虽然只是勾股定理的实际应用这一知识点,但是涉及生产生活的各个方面,受时间约束无法一一列举,本课中的三个例子缺乏开放性.
补救措施:在问题设计上,进一步注意层次性、开放性,并增加每一类题目的变式训练题,提高学生分析问题和解决问题的能力.同时,在后续学习中加强与勾股定理的综合运用训练.
5 / 6
第2课时
一、教学目标
【知识与技能】
1.能应用勾股定理计算直角三角形的边长.
2.能应用勾股定理解决简单的实际问题.
3.能说出勾股定理,能运用勾股定理的数学模型解决现实世界的实际问题.
【过程与方法】
1.通过从实际问题中抽象出直角三角形这一模型,强化转化思想,培养学生解决现实问题的意识和能力.
2.经历探究勾股定理在实际问题中的应用过程,进一步体会勾股定理的应用方法.
【情感态度与价值观】
在例题分析和解决过程中,让学生感受勾股定理在实际生活中的应用.同时在学习过程中体会获得成功的喜悦,提高学生学习数学的兴趣和信心.
二、课型
新授课
三、课时
第2课时 共3课时
四、教学重难点
【教学重点】
运用勾股定理解决实际问题.
【教学难点】
勾股定理的灵活运用.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、直尺、练习本、三角形模型.
六、教学过程
(一)导入新课(出示课件2)
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.
离开原处6尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺?
示意图见课件,就是求AD的长
教师:这节课我们就来学习用勾股定理解决实际问题,学完本节课知识后,自己再想想怎么计算此题吧!
(二)探索新知
1.出示课件4-6,探究勾股定理解决线段长度问题
教师问:一个门框的尺寸如图所示,一块长3m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
学生答:不能,因为木板的长3m大于2m,宽2.2m大于1m.
教师问:木板能横着或竖着从门框通过吗?
学生答:不能.
教师问:这个门框能通过的最大长度是多少?
学生讨论后回答:如图所示,小于线段AC的长度才可以.
教师问:怎样判定这块木板能否通过木框?
学生回答:求出斜边AC的长,与木板的宽比较.
师生一起解答:
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所以木板能从门框内通过.
出示课件7,学生自主练习后口答,教师订正.
2.出示课件8-9,探究勾股定理解决线段移动问题
教师问:如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.求梯子的底端B距墙角O多少米?
学生回答:
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
教师问:如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
学生回答:在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
OD=≈1.77.BD=OD-OB≈1.77-1=0.77
答:梯子底端B也外移约0.77米.
出示课件10,学生自主练习后口答,教师订正.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件12-19)
练习课件第12-19页题目,约用时20分钟.
(四)课堂小结(出示课件20)
用勾股定理计算时,要先画好图形,并标好图形,理清各边之间的关系,再灵活运用勾股定理计算.在利用勾股定理进行有关计算和证明时,要注意运用方程的思想;求直角三角形有关线段的长,有时还要运用转化的数学思想,或利用添加辅助线的方法构造直角三角形,再运用勾股定理求解.
(五)课前预习
预习下节课(17.1第3课时)的相关内容.
知道如何在数轴上标出无理数及构造直角三角形表示出无理数.
七、课后作业
教材第26页练习第1,2题.
八、板书设计
勾股定理 第2课时
1.解决线段长度问题
2.解决线段移动问题
3.例题讲解
九、教学反思
成功之处:本节课运用勾股定理解决实际问题,整节课注重基础,通过分类探索,由浅入深,注重讲练结合,引导学生独立分析,自主学习,提高学生运用勾股定理解决简单问题的能力.虽然只是勾股定理的实际应用这一知识点,但是涉及生产生活的各个方面,受时间约束无法一一列举,本课中的三个例子缺乏开放性.
补救措施:在问题设计上,进一步注意层次性、开放性,并增加每一类题目的变式训练题,提高学生分析问题和解决问题的能力.同时,在后续学习中加强与勾股定理的综合运用训练.
5 / 6
