人教版八年级数学下册 17.1 勾股定理(第3课时)教案
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理(第3课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:50:01 | ||
图片预览

文档简介
17.1 勾股定理
第3课时
一、教学目标
【知识与技能】
1.利用勾股定理,能在数轴上找到表示无理数的点.
2.进一步学习将实际问题转化为直角三角形的数学模型,并能用勾股定理解决简单的实际问题.
【过程与方法】
1.经历在数轴上寻找表示无理数的点的过程,发展学生灵活运用勾股定理解决问题的能力.
2.在用勾股定理解决实际问题的过程中,体验解决问题的策略,发展学生的动手操作能力和创新精神.
3.在解决实际问题的过程中,学会与人合作,并能与他人交流思维过程和结果,形成反思的意识.
【情感态度与价值观】
1.在利用勾股定理寻找数轴上表示无理数的点的过程中,体会勾股定理的重要作用,并从中获得成功的体验,锻炼克服困难的意志,建立自信心.
2.在解决实际问题的过程中,形成实事求是的态度以及进行质疑和独立思考的习惯.
二、课型
新授课
三、课时
第3课时 共3课时
四、教学重难点
【教学重点】
能利用勾股定理在数轴上表示无理数.
【教学难点】
利用勾股定理寻找直角三角形中长度为无理数的线段.
五、课前准备
教师:课件、三角尺、直尺、圆规等.
学生:复习尺规作图的有关知识,准备三角板、直尺、圆规、铅笔.
六、教学过程
(一)导入新课(出示课件2)
欣赏课件中海螺的图片:
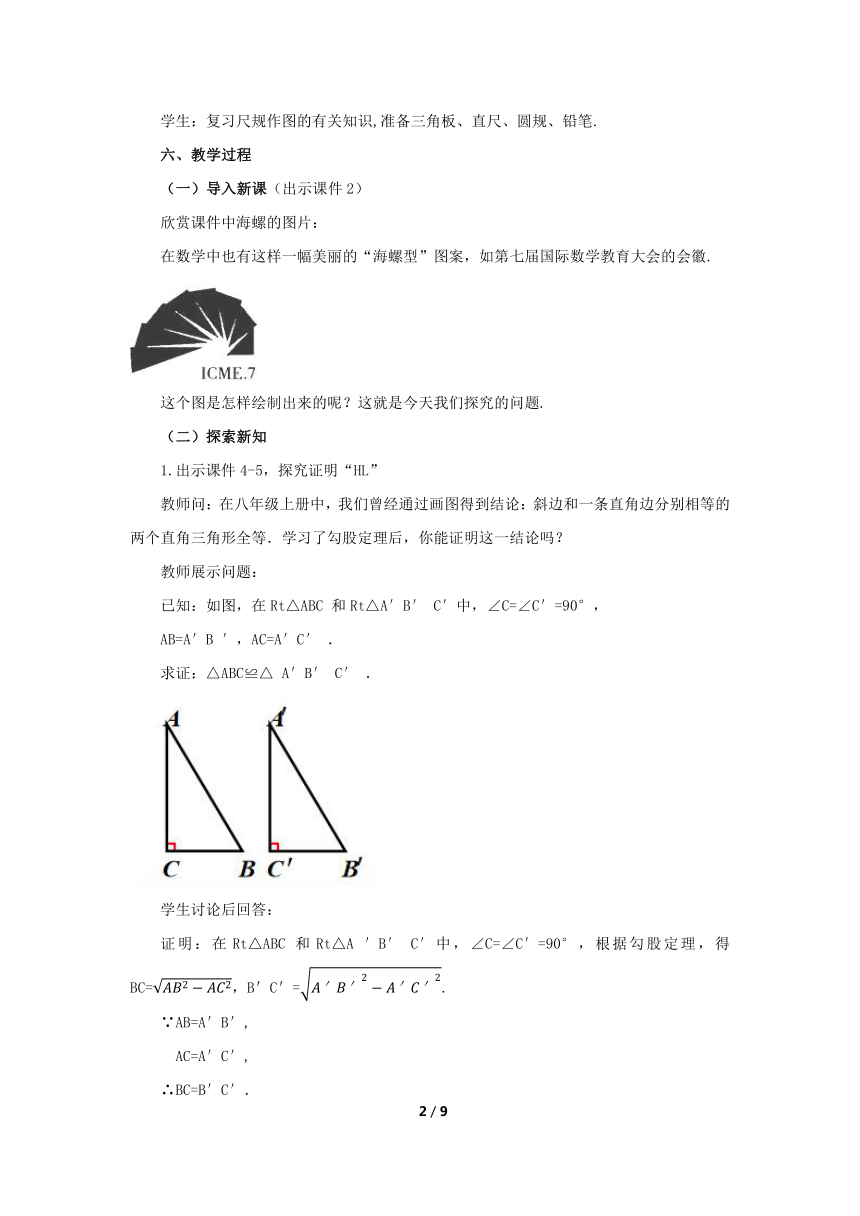
在数学中也有这样一幅美丽的“海螺型”图案,如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?这就是今天我们探究的问题.
(二)探索新知
1.出示课件4-5,探究证明“HL”
教师问:在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
教师展示问题:
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,∠C=∠C′=90°,
AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
学生讨论后回答:
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,根据勾股定理,得BC=,B'C'=.
∵AB=A′B′,
AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
2.出示课件6-8,探究利用勾股定理在数轴上确定无理数
教师问:你能在数轴上表示出的点吗?-呢?
师生一起解答:(出示课件6) 放幻灯片,展示作图过程.
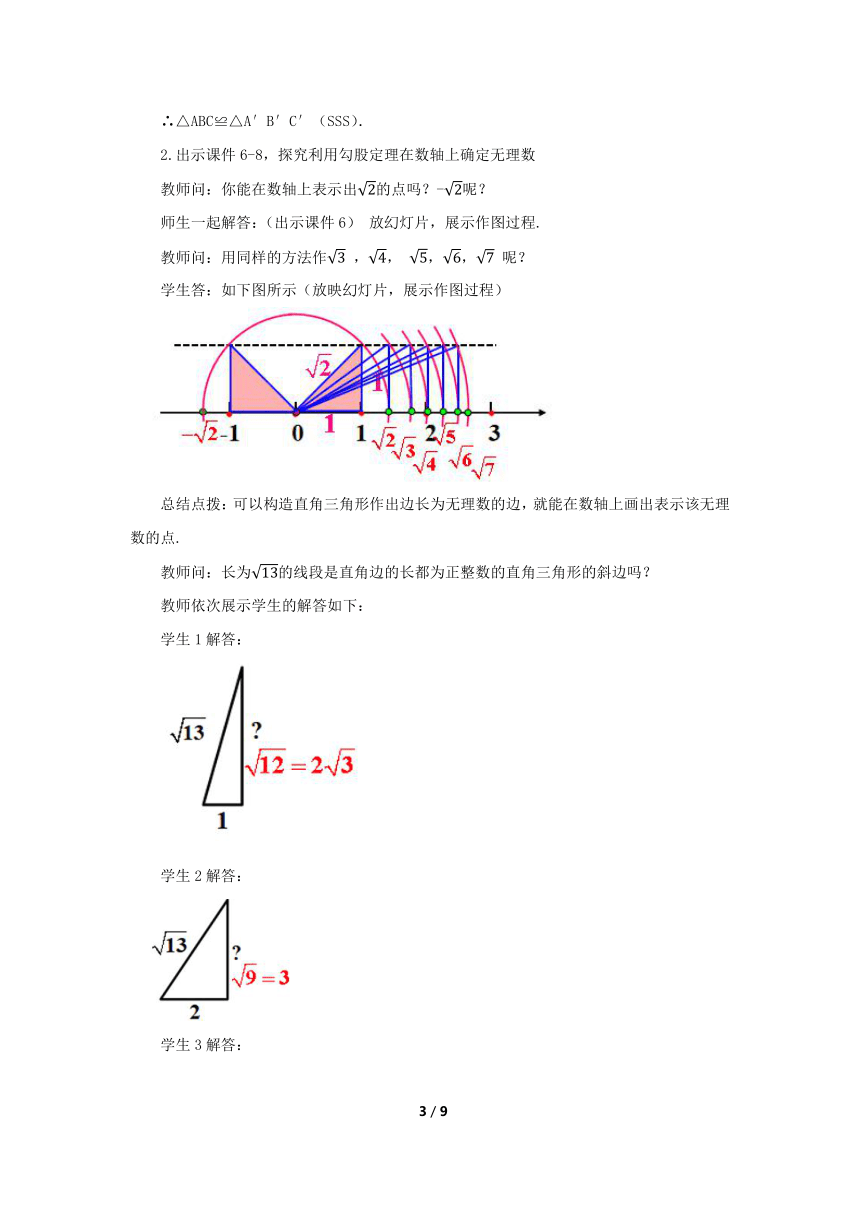
教师问:用同样的方法作 , ,, 呢?
学生答:如下图所示(放映幻灯片,展示作图过程)
总结点拨:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
教师问:长为的线段是直角边的长都为正整数的直角三角形的斜边吗?
教师依次展示学生的解答如下:
学生1解答:
学生2解答:
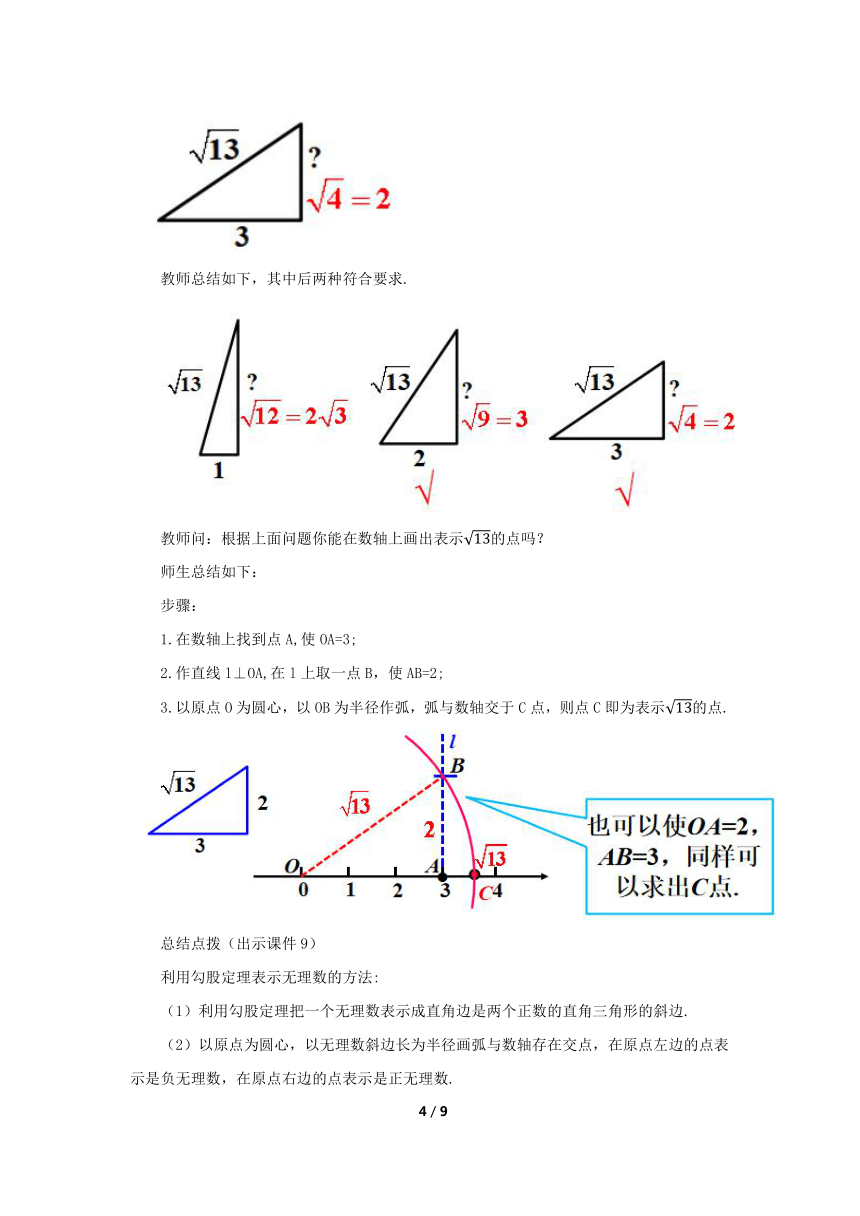
学生3解答:
教师总结如下,其中后两种符合要求.
教师问:根据上面问题你能在数轴上画出表示的点吗?
师生总结如下:
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示的点.
总结点拨(出示课件9)
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
考点1:利用勾股定理在数轴上确定无理数的点
在数轴上作出表示的点.(出示课件10)
师生共同讨论解答如下:
解:作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,使AB=4,那么OB=;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=.
如图,在数轴上,点C为表示的点.
出示课件11,学生自主练习后口答,教师订正.
3.出示课件12-13,探究利用勾股定理在网格上做长度为无理数的线段
教师问:在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为的线段AB.
教师展示答案如下:
学生1回答:
学生2解答:
学生3解答:
教师追问:如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为的线段
学生讨论后回答:如图所示:
总结点拨:(出示课件13)
勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
考点1:利用勾股定理在网格上作线段
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为的线段?(出示课件14)
学生独立思考后,师生共同解答.
解:如图所示,有8条.
总结点拨:(出示课件14)
一个点一个点地找,不要漏解.
出示课件15,学生自主练习后口答,教师订正.
4.利用勾股定理在折叠问题中求线段的长度
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,求AM的长.(出示课件16)
学生独立思考后,师生共同解答.
解:连接BM,MB′.设AM=x,
在Rt△ABM中,AB2+AM2=BM2.
在Rt△MDB′中,MD2+DB′2=MB′2.
∵MB=MB′,∴AB2+AM2=MD2+DB′2,
即92+x2=(9-x)2+(9-3)2,
解得x=2.即AM=2.
师生共同归纳如下:(出示课件17)
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线段或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
出示课件18,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件19-26)
练习课件第19-26页题目,约用时20分钟.
(四)课堂小结(出示课件27)
师生共同回顾本节课所学主要内容:
1.用勾股定理在数轴上表示无理数,构造长为无理数的线段放在直角三角形中,有时是直角边,有时是斜边.
2.求不规则图形的面积,应用割补法把图形分解为特殊图形,四边形中常常通过作辅助线构造直角三角形,以利用勾股定理.
(五)课前预习
预习下节课(17.2第1课时)的相关内容.
知道勾股定理的逆定理和原命题、逆命题的定义
七、课后作业
教材第27页练习第1,2题.
八、板书设计
勾股定理 第3课时
1. 利用勾股定理证明HL定理
2. 利用勾股定理在数轴上表示无理数
3. 利用勾股定理在网格上做长度为无理数的线段
考点1
4. 利用勾股定理在折叠问题中求线段的长度
5. 例题讲解
九、教学反思
成功之处:本节课注重数学与生活的联系,注重数学知识的应用,从学生认知规律和接受水平出发,循序渐进地引入新课,成功地引导学生会将长为无理数的线段看成一个直角三角形的斜边,再按照尺规作图的要求,在数轴上找出表示无理数的点.由于学生尺规作图的能力较差,学生在确定了作图思路之后,却难以按照尺规作图的步骤完成作图.
补救措施:教师指导在数轴上找出表示无理数的点,示范作图步骤.教学中,根据学生的基础情况,适当进行复习,帮助学生解决学习中的困难.
11 / 11
第3课时
一、教学目标
【知识与技能】
1.利用勾股定理,能在数轴上找到表示无理数的点.
2.进一步学习将实际问题转化为直角三角形的数学模型,并能用勾股定理解决简单的实际问题.
【过程与方法】
1.经历在数轴上寻找表示无理数的点的过程,发展学生灵活运用勾股定理解决问题的能力.
2.在用勾股定理解决实际问题的过程中,体验解决问题的策略,发展学生的动手操作能力和创新精神.
3.在解决实际问题的过程中,学会与人合作,并能与他人交流思维过程和结果,形成反思的意识.
【情感态度与价值观】
1.在利用勾股定理寻找数轴上表示无理数的点的过程中,体会勾股定理的重要作用,并从中获得成功的体验,锻炼克服困难的意志,建立自信心.
2.在解决实际问题的过程中,形成实事求是的态度以及进行质疑和独立思考的习惯.
二、课型
新授课
三、课时
第3课时 共3课时
四、教学重难点
【教学重点】
能利用勾股定理在数轴上表示无理数.
【教学难点】
利用勾股定理寻找直角三角形中长度为无理数的线段.
五、课前准备
教师:课件、三角尺、直尺、圆规等.
学生:复习尺规作图的有关知识,准备三角板、直尺、圆规、铅笔.
六、教学过程
(一)导入新课(出示课件2)
欣赏课件中海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?这就是今天我们探究的问题.
(二)探索新知
1.出示课件4-5,探究证明“HL”
教师问:在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
教师展示问题:
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,∠C=∠C′=90°,
AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
学生讨论后回答:
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,根据勾股定理,得BC=,B'C'=.
∵AB=A′B′,
AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
2.出示课件6-8,探究利用勾股定理在数轴上确定无理数
教师问:你能在数轴上表示出的点吗?-呢?
师生一起解答:(出示课件6) 放幻灯片,展示作图过程.
教师问:用同样的方法作 , ,, 呢?
学生答:如下图所示(放映幻灯片,展示作图过程)
总结点拨:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
教师问:长为的线段是直角边的长都为正整数的直角三角形的斜边吗?
教师依次展示学生的解答如下:
学生1解答:
学生2解答:
学生3解答:
教师总结如下,其中后两种符合要求.
教师问:根据上面问题你能在数轴上画出表示的点吗?
师生总结如下:
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示的点.
总结点拨(出示课件9)
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
考点1:利用勾股定理在数轴上确定无理数的点
在数轴上作出表示的点.(出示课件10)
师生共同讨论解答如下:
解:作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,使AB=4,那么OB=;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=.
如图,在数轴上,点C为表示的点.
出示课件11,学生自主练习后口答,教师订正.
3.出示课件12-13,探究利用勾股定理在网格上做长度为无理数的线段
教师问:在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为的线段AB.
教师展示答案如下:
学生1回答:
学生2解答:
学生3解答:
教师追问:如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为的线段
学生讨论后回答:如图所示:
总结点拨:(出示课件13)
勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
考点1:利用勾股定理在网格上作线段
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为的线段?(出示课件14)
学生独立思考后,师生共同解答.
解:如图所示,有8条.
总结点拨:(出示课件14)
一个点一个点地找,不要漏解.
出示课件15,学生自主练习后口答,教师订正.
4.利用勾股定理在折叠问题中求线段的长度
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,求AM的长.(出示课件16)
学生独立思考后,师生共同解答.
解:连接BM,MB′.设AM=x,
在Rt△ABM中,AB2+AM2=BM2.
在Rt△MDB′中,MD2+DB′2=MB′2.
∵MB=MB′,∴AB2+AM2=MD2+DB′2,
即92+x2=(9-x)2+(9-3)2,
解得x=2.即AM=2.
师生共同归纳如下:(出示课件17)
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线段或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
出示课件18,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件19-26)
练习课件第19-26页题目,约用时20分钟.
(四)课堂小结(出示课件27)
师生共同回顾本节课所学主要内容:
1.用勾股定理在数轴上表示无理数,构造长为无理数的线段放在直角三角形中,有时是直角边,有时是斜边.
2.求不规则图形的面积,应用割补法把图形分解为特殊图形,四边形中常常通过作辅助线构造直角三角形,以利用勾股定理.
(五)课前预习
预习下节课(17.2第1课时)的相关内容.
知道勾股定理的逆定理和原命题、逆命题的定义
七、课后作业
教材第27页练习第1,2题.
八、板书设计
勾股定理 第3课时
1. 利用勾股定理证明HL定理
2. 利用勾股定理在数轴上表示无理数
3. 利用勾股定理在网格上做长度为无理数的线段
考点1
4. 利用勾股定理在折叠问题中求线段的长度
5. 例题讲解
九、教学反思
成功之处:本节课注重数学与生活的联系,注重数学知识的应用,从学生认知规律和接受水平出发,循序渐进地引入新课,成功地引导学生会将长为无理数的线段看成一个直角三角形的斜边,再按照尺规作图的要求,在数轴上找出表示无理数的点.由于学生尺规作图的能力较差,学生在确定了作图思路之后,却难以按照尺规作图的步骤完成作图.
补救措施:教师指导在数轴上找出表示无理数的点,示范作图步骤.教学中,根据学生的基础情况,适当进行复习,帮助学生解决学习中的困难.
11 / 11
