人教版八年级数学下册17.2 勾股定理的逆定理(第1课时)教案
文档属性
| 名称 | 人教版八年级数学下册17.2 勾股定理的逆定理(第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 198.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览


文档简介
17.2 勾股定理的逆定理
第1课时
一、教学目标
【知识与技能】
1.理解并能证明勾股定理的逆定理.
2.理解原命题、逆命题、逆定理的概念.
3.会认识并判断勾股数,掌握勾股定理的逆定理,并能灵活应用逆定理判定一个三角形是否为直角三角形.
【过程与方法】
1.通过对勾股定理的逆定理的探索,经历知识发生、发展和形成的过程.
2.通过用三角形的三边的数量关系来判断三角形的形状,体验数形结合方法的应用.
【情感态度与价值观】
1.通过用三边之间的数量关系来判断三角形的形状,体验数与形的内在联系,感受定理与逆定理之间的和谐辩证统一的关系.
2.在对勾股定理的逆定理的探索中,培养了学生的交流、合作的意识和严谨的学习态度,同时感悟勾股定理和逆定理的应用价值.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
勾股定理的逆定理的应用.
【教学难点】
勾股定理的逆定理的证明.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、绳子、铅笔、直尺、练习本.
六、教学过程
(一)导入新课(出示课件2)
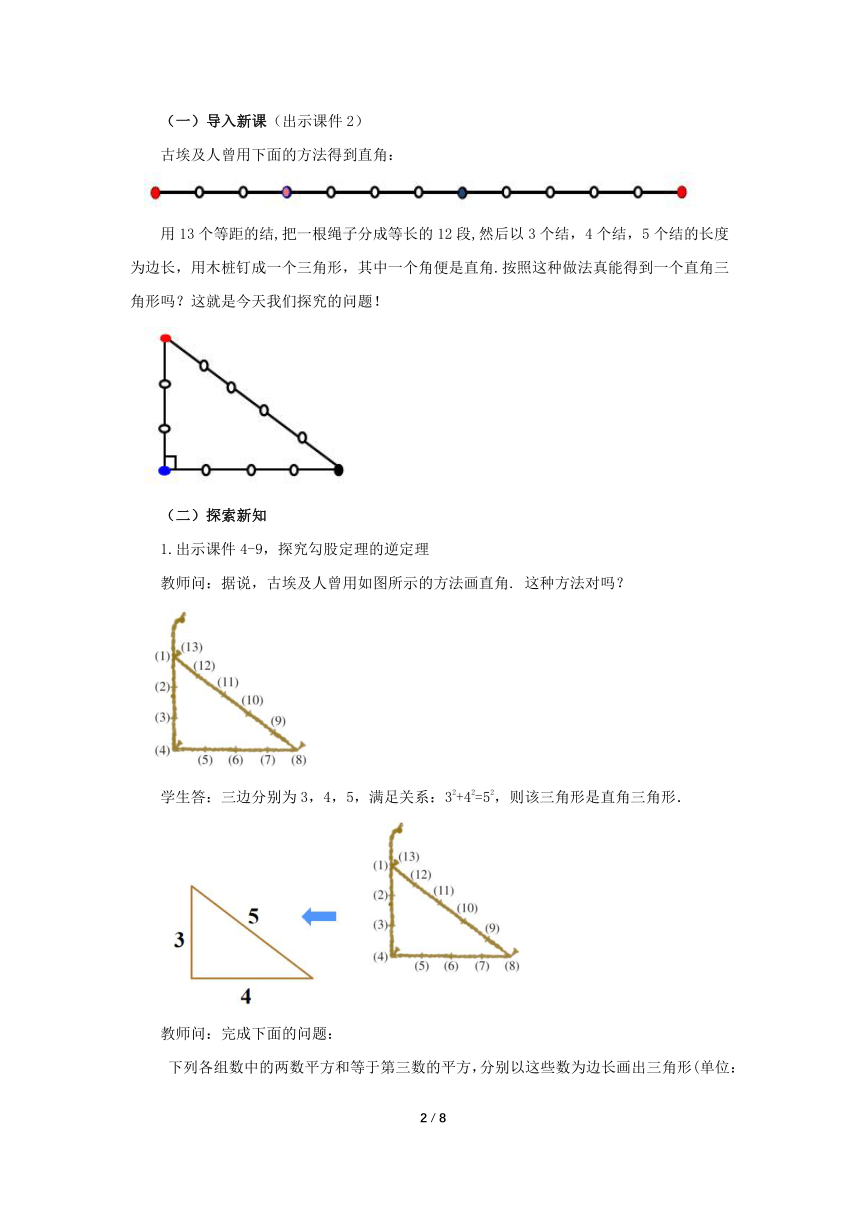
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.按照这种做法真能得到一个直角三角形吗?这就是今天我们探究的问题!
(二)探索新知
1.出示课件4-9,探究勾股定理的逆定理
教师问:据说,古埃及人曾用如图所示的方法画直角. 这种方法对吗?
学生答:三边分别为3,4,5,满足关系:32+42=52,则该三角形是直角三角形.
教师问:完成下面的问题:
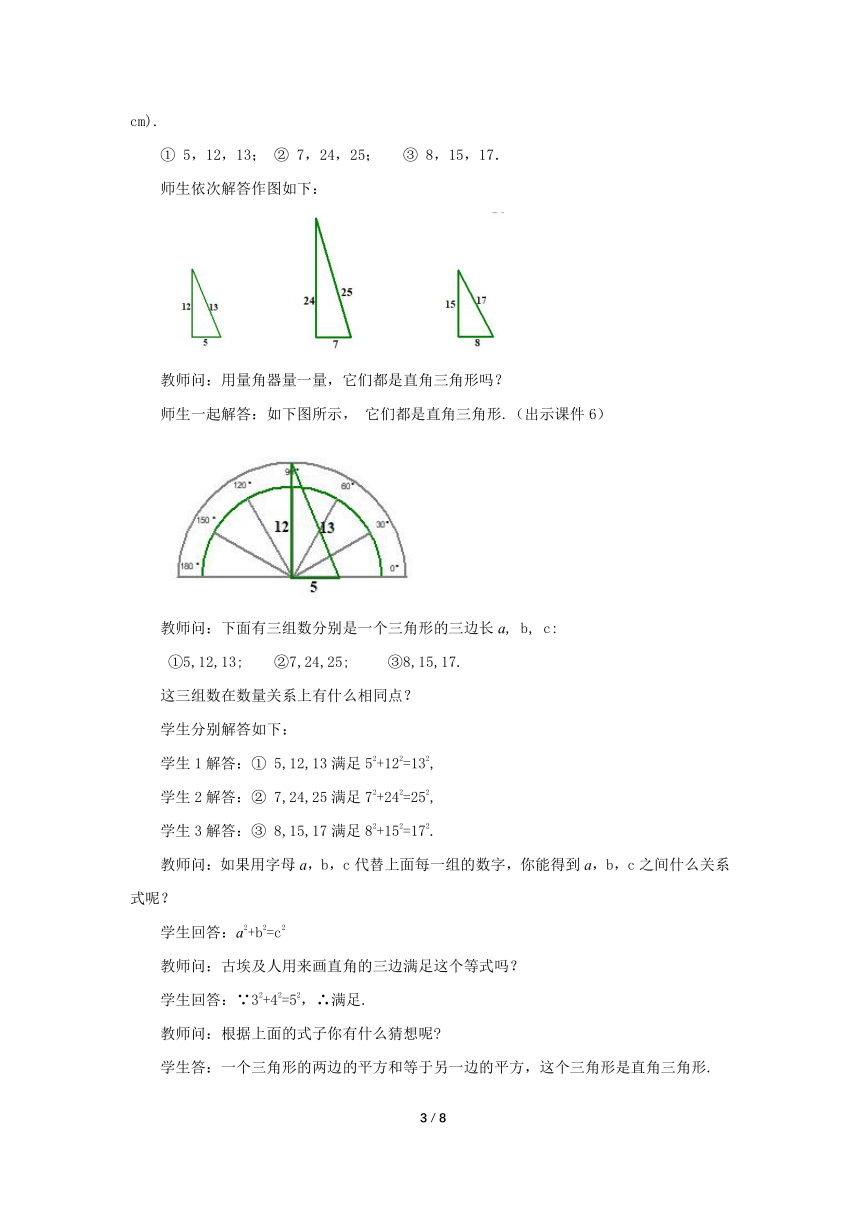
下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
师生依次解答作图如下:
教师问:用量角器量一量,它们都是直角三角形吗?
师生一起解答:如下图所示, 它们都是直角三角形.(出示课件6)
教师问:下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
这三组数在数量关系上有什么相同点?
学生分别解答如下:
学生1解答:① 5,12,13满足52+122=132,
学生2解答:② 7,24,25满足72+242=252,
学生3解答:③ 8,15,17满足82+152=172.
教师问:如果用字母a,b,c代替上面每一组的数字,你能得到a,b,c之间什么关系式呢?
学生回答:a2+b2=c2
教师问:古埃及人用来画直角的三边满足这个等式吗?
学生回答:∵32+42=52,∴满足.
教师问:根据上面的式子你有什么猜想呢
学生答:一个三角形的两边的平方和等于另一边的平方,这个三角形是直角三角形.
教师总结如下:由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
教师问:你觉得这个猜想严谨吗?为什么?
学生1回答:我觉得这个猜想不准确,因为测量结果可能有误差.
学生2回答:我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
教师问:试着完成下面的题目。
展示问题:已知:如图,在△ABC中,AB=c,BC=a,CA=b,并且a2+b2=c2 .求证:∠C=90°.
师生共同解答如下:
证明:作 A1B1C1, 使∠C1=90°,B1C1=a,C1A1=b. 根据勾股定理,则有A1B12=B1C12+C1A1 2=a2+b2. ∵a2+b2=c2, ∴A1B1=c,∴AB=A1B1.
在△ABC和△A1B1C1中,
BC=B1C1,
CA=C1A1,
AB=A1B1.
∴ ABC≌ A1B1C1.
∴∠C=∠C1=90°.
教师总结归纳:(出示课件10)
勾股定理的逆定理:如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
教师追问:你能利用符号语言描述一下上面的定理吗?
师生一起总结如下:
符号语言:
在△ABC中,若a2+b2=c2
则△ABC是直角三角形.
教师总结点拨:(出示课件11)
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
考点1:利用勾股定理的逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是,
那么哪一个角是直角?(出示课件12)
(1) a=15 , b=8 ,c=17; (2) a=13 ,b=14 ,c=15.
师生共同讨论解答如下:
学生1解:
(1)∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
学生2解:
(2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
师生总结点拨:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
出示课件13,学生自主练习后口答,教师订正.
考点2:勾股定理的逆定理和乘法公式判断三角形
若△ABC的三边a,b,c,且a+b=4,ab=1,c=,试说明△ABC是直角三角形.(出示课件14)
学生独立思考后,师生共同解答.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
出示课件15,学生自主练习后口答,教师订正.
2.出示课件16,探究勾股数
教师问:如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.你能找到满足a2+b2=c2的三个数均为正整数吗?
学生1回答:可以找到,例如3,4,5.
学生2回答:可以找到,例如5,12,13.
教师问:如果满足a2+b2=c2的三个均为正整数,我们把具有这种性质的一组数叫做勾股数.你能举出实际的例子吗?
学生1回答:3,4,5. 5,12,13
学生2回答:6,8,10. 7,24,25.
学生3回答: 8,15,17. 9,40,41.
学生4回答:10,24,26
教师问:勾股数有很多,那么如何快速找勾股数呢?
师生共同解答如下:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
出示课件17,学生自主练习,教师给出答案。
3.出示课件18,互逆命题和互逆定理
教师问:看下面的两个命题:
命题1如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你发现了什么?
师生共同解答如下:发现:两个命题的条件和结论如下所示:
教师问:两个命题的条件和结论有怎样的关系?
学生回答:两个命题的条件和结论有如下联系:它们是题设和结论正好相反的两个命题.
教师总结归纳:(出示课件20)
定义:题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
归纳总结:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
出示课件21,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件22-27)
练习课件第22-27页题目,约用时20分钟
(四)课堂小结(出示课件28)
师生共同回顾本节课所学主要内容:
(1)已知一个三角形的三边长,利用勾股定理的逆定理来判定这个三角形是不是直角三角形.
(2)一个命题一定有逆命题,一个定理不一定有逆定理.
(3)三个数满足勾股数的两个条件:①三个数必须满足较小的两个数的平方和等于最大的一个数的平方;②三个数必须都是正整数.
(4)解题时,注意勾股定理与其逆定理的区别.勾股定理是在直角三角形中运用的,而勾股定理的逆定理是判断一个三角形是不是直角三角形的.
(五)课前预习
预习下节课(17.2第2课时)的相关内容.
知道利用勾股定理及其逆定理解决实际问题的方法
七、课后作业
教材第33页练习第1,2,3题.
八、板书设计
17.2 勾股定理的逆定理
第1课时
1.勾股定理的逆定理
(1)归纳猜想
(2)原命题、逆命题
(3)勾股定理的逆定理的证明
2.勾股数
3.互逆命题和互逆定理
考点1 考点2
4.例题讲解
九、教学反思
成功之处:
1.本节课以“提出问题——解决问题”为主线,以学生的自主探索学习为中心,从解决问题的完成情况看,知识目标完全达到,能力目标基本实现,情感目标基本实现.
2.在本节课教学中,充分发挥学生在教学中的主体作用,教师不能一味地“讲知识”,而是应用启发式的原则,给学生指明学习目标和方向,让学生去自主探究,注重了知识上的及时巩固,也侧重了学生各方面的素质的培养.
不足之处:
1.在重难点的突破上,还应加一些递进的习题,降低题的难度,使优生学好,中等生也能跟上.同时,缺少了板书示范,不利于学生养成良好的书写习惯.
2.本节课内容较多,由于时间紧,还是不敢放手,总是牵着学生走,结果学生的积极性没有充分调动起来,还需要注意教师精讲,留足时间让学生探究.
1 / 11
第1课时
一、教学目标
【知识与技能】
1.理解并能证明勾股定理的逆定理.
2.理解原命题、逆命题、逆定理的概念.
3.会认识并判断勾股数,掌握勾股定理的逆定理,并能灵活应用逆定理判定一个三角形是否为直角三角形.
【过程与方法】
1.通过对勾股定理的逆定理的探索,经历知识发生、发展和形成的过程.
2.通过用三角形的三边的数量关系来判断三角形的形状,体验数形结合方法的应用.
【情感态度与价值观】
1.通过用三边之间的数量关系来判断三角形的形状,体验数与形的内在联系,感受定理与逆定理之间的和谐辩证统一的关系.
2.在对勾股定理的逆定理的探索中,培养了学生的交流、合作的意识和严谨的学习态度,同时感悟勾股定理和逆定理的应用价值.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
勾股定理的逆定理的应用.
【教学难点】
勾股定理的逆定理的证明.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、绳子、铅笔、直尺、练习本.
六、教学过程
(一)导入新课(出示课件2)
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.按照这种做法真能得到一个直角三角形吗?这就是今天我们探究的问题!
(二)探索新知
1.出示课件4-9,探究勾股定理的逆定理
教师问:据说,古埃及人曾用如图所示的方法画直角. 这种方法对吗?
学生答:三边分别为3,4,5,满足关系:32+42=52,则该三角形是直角三角形.
教师问:完成下面的问题:
下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
师生依次解答作图如下:
教师问:用量角器量一量,它们都是直角三角形吗?
师生一起解答:如下图所示, 它们都是直角三角形.(出示课件6)
教师问:下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
这三组数在数量关系上有什么相同点?
学生分别解答如下:
学生1解答:① 5,12,13满足52+122=132,
学生2解答:② 7,24,25满足72+242=252,
学生3解答:③ 8,15,17满足82+152=172.
教师问:如果用字母a,b,c代替上面每一组的数字,你能得到a,b,c之间什么关系式呢?
学生回答:a2+b2=c2
教师问:古埃及人用来画直角的三边满足这个等式吗?
学生回答:∵32+42=52,∴满足.
教师问:根据上面的式子你有什么猜想呢
学生答:一个三角形的两边的平方和等于另一边的平方,这个三角形是直角三角形.
教师总结如下:由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
教师问:你觉得这个猜想严谨吗?为什么?
学生1回答:我觉得这个猜想不准确,因为测量结果可能有误差.
学生2回答:我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
教师问:试着完成下面的题目。
展示问题:已知:如图,在△ABC中,AB=c,BC=a,CA=b,并且a2+b2=c2 .求证:∠C=90°.
师生共同解答如下:
证明:作 A1B1C1, 使∠C1=90°,B1C1=a,C1A1=b. 根据勾股定理,则有A1B12=B1C12+C1A1 2=a2+b2. ∵a2+b2=c2, ∴A1B1=c,∴AB=A1B1.
在△ABC和△A1B1C1中,
BC=B1C1,
CA=C1A1,
AB=A1B1.
∴ ABC≌ A1B1C1.
∴∠C=∠C1=90°.
教师总结归纳:(出示课件10)
勾股定理的逆定理:如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
教师追问:你能利用符号语言描述一下上面的定理吗?
师生一起总结如下:
符号语言:
在△ABC中,若a2+b2=c2
则△ABC是直角三角形.
教师总结点拨:(出示课件11)
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
考点1:利用勾股定理的逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是,
那么哪一个角是直角?(出示课件12)
(1) a=15 , b=8 ,c=17; (2) a=13 ,b=14 ,c=15.
师生共同讨论解答如下:
学生1解:
(1)∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
学生2解:
(2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
师生总结点拨:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
出示课件13,学生自主练习后口答,教师订正.
考点2:勾股定理的逆定理和乘法公式判断三角形
若△ABC的三边a,b,c,且a+b=4,ab=1,c=,试说明△ABC是直角三角形.(出示课件14)
学生独立思考后,师生共同解答.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
出示课件15,学生自主练习后口答,教师订正.
2.出示课件16,探究勾股数
教师问:如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.你能找到满足a2+b2=c2的三个数均为正整数吗?
学生1回答:可以找到,例如3,4,5.
学生2回答:可以找到,例如5,12,13.
教师问:如果满足a2+b2=c2的三个均为正整数,我们把具有这种性质的一组数叫做勾股数.你能举出实际的例子吗?
学生1回答:3,4,5. 5,12,13
学生2回答:6,8,10. 7,24,25.
学生3回答: 8,15,17. 9,40,41.
学生4回答:10,24,26
教师问:勾股数有很多,那么如何快速找勾股数呢?
师生共同解答如下:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
出示课件17,学生自主练习,教师给出答案。
3.出示课件18,互逆命题和互逆定理
教师问:看下面的两个命题:
命题1如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你发现了什么?
师生共同解答如下:发现:两个命题的条件和结论如下所示:
教师问:两个命题的条件和结论有怎样的关系?
学生回答:两个命题的条件和结论有如下联系:它们是题设和结论正好相反的两个命题.
教师总结归纳:(出示课件20)
定义:题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
归纳总结:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
出示课件21,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件22-27)
练习课件第22-27页题目,约用时20分钟
(四)课堂小结(出示课件28)
师生共同回顾本节课所学主要内容:
(1)已知一个三角形的三边长,利用勾股定理的逆定理来判定这个三角形是不是直角三角形.
(2)一个命题一定有逆命题,一个定理不一定有逆定理.
(3)三个数满足勾股数的两个条件:①三个数必须满足较小的两个数的平方和等于最大的一个数的平方;②三个数必须都是正整数.
(4)解题时,注意勾股定理与其逆定理的区别.勾股定理是在直角三角形中运用的,而勾股定理的逆定理是判断一个三角形是不是直角三角形的.
(五)课前预习
预习下节课(17.2第2课时)的相关内容.
知道利用勾股定理及其逆定理解决实际问题的方法
七、课后作业
教材第33页练习第1,2,3题.
八、板书设计
17.2 勾股定理的逆定理
第1课时
1.勾股定理的逆定理
(1)归纳猜想
(2)原命题、逆命题
(3)勾股定理的逆定理的证明
2.勾股数
3.互逆命题和互逆定理
考点1 考点2
4.例题讲解
九、教学反思
成功之处:
1.本节课以“提出问题——解决问题”为主线,以学生的自主探索学习为中心,从解决问题的完成情况看,知识目标完全达到,能力目标基本实现,情感目标基本实现.
2.在本节课教学中,充分发挥学生在教学中的主体作用,教师不能一味地“讲知识”,而是应用启发式的原则,给学生指明学习目标和方向,让学生去自主探究,注重了知识上的及时巩固,也侧重了学生各方面的素质的培养.
不足之处:
1.在重难点的突破上,还应加一些递进的习题,降低题的难度,使优生学好,中等生也能跟上.同时,缺少了板书示范,不利于学生养成良好的书写习惯.
2.本节课内容较多,由于时间紧,还是不敢放手,总是牵着学生走,结果学生的积极性没有充分调动起来,还需要注意教师精讲,留足时间让学生探究.
1 / 11
