人教版八年级数学下册 18.1.1 平行四边形的性质(第1课时)教案
文档属性
| 名称 | 人教版八年级数学下册 18.1.1 平行四边形的性质(第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 156.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 21:51:11 | ||
图片预览


文档简介
18.1.1 平行四边形的性质
第1课时
一、教学目标
【知识与技能】
1.理解平行四边形的定义及有关概念.
2.探究并掌握平行四边形的对边相等、对角相等的性质,利用平行四边形的性质进行简单的计算和证明.
3.了解平行线间距离的概念.
【过程与方法】
1.经历利用平行四边形描述、观察世界的过程,发展学生的形象思维和抽象思维.
2.在进行性质探索的活动过程中,发展学生的探究能力.
3.在性质应用的过程中,提高学生运用数学知识解决实际问题的能力,培养学生的推理能力和逻辑思维能力.
【情感态度与价值观】
在性质应用过程中培养独立思考的习惯,让学生在观察、合作、讨论、交流中感受数学的实际应用价值,同时培养学生善于发现、积极思考、合作学习的学习态度.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
平行四边形边、角的性质探索和证明.
【教学难点】
如何添加辅助线将平行四边形问题转化成三角形问题解决的思想方法.
五、课前准备
教师:课件、三角尺、直尺、教学中出示的教学插图和例题的投影图片等.
学生:三角尺、铅笔、方格纸,量角器,刻度尺.
六、教学过程
(一)导入新课(出示课件2)
我们一起来观察下图中的小区的伸缩门,庭院的竹篱笆等图,它们是什么几何图形
(二)探索新知
1.出示课件4-6,探究平行四边形的定义
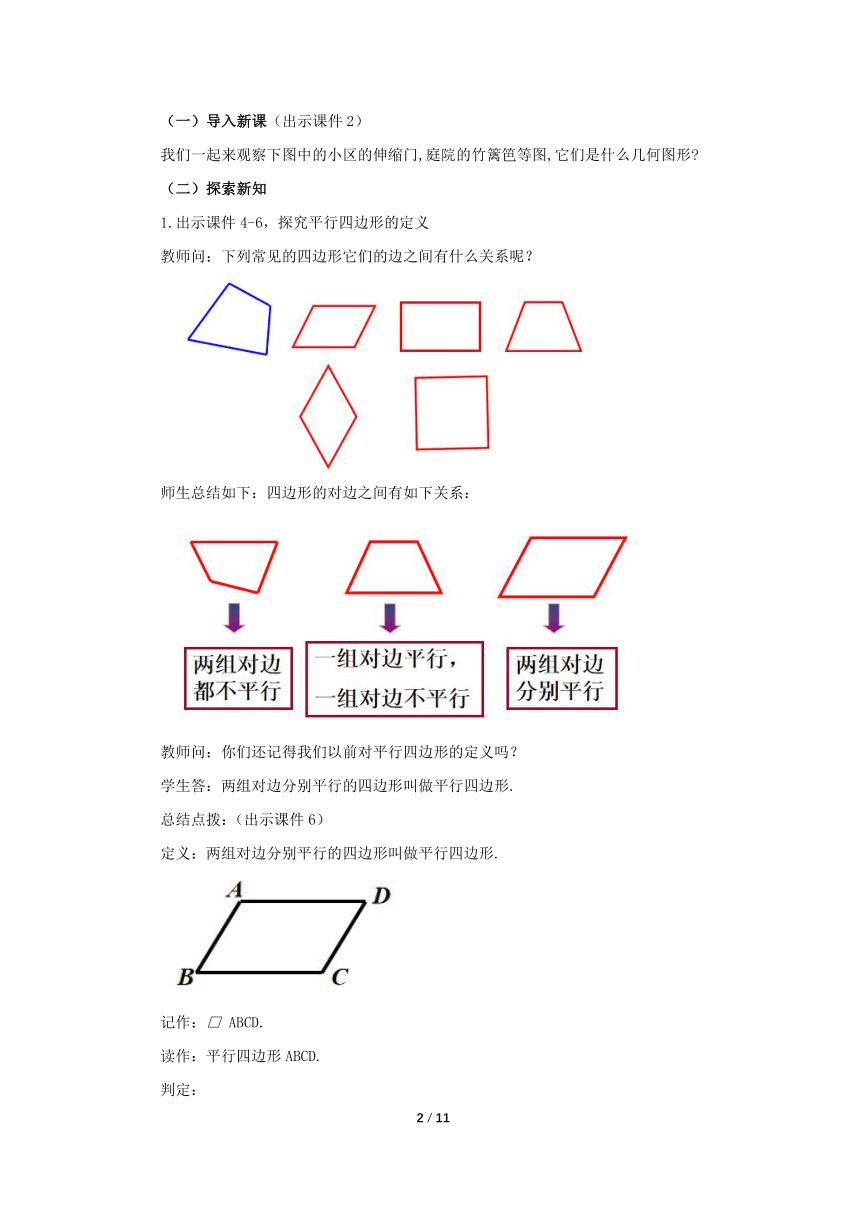
教师问:下列常见的四边形它们的边之间有什么关系呢?
师生总结如下:四边形的对边之间有如下关系:
教师问:你们还记得我们以前对平行四边形的定义吗?
学生答:两组对边分别平行的四边形叫做平行四边形.
总结点拨:(出示课件6)
定义:两组对边分别平行的四边形叫做平行四边形.
记作:□ ABCD.
读作:平行四边形ABCD.
判定:
∵AB∥CD, AD∥BC,
∴四边形ABCD是平行四边形.
性质:
∵四边形ABCD是平行四边形,
∴AB∥CD, AD∥BC,
教师强调:图形中字母的标识顺序应为顺时针方向或逆时针方向.
考点1:利用平行四边形的定义判断平行四边形
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.并把它们表示出来.(出示课件7)
师生共同讨论解答如下:
教师依次展示学生答案:
学生1解答:∵DC∥FH ∥ AB,DA∥ EG∥ CB,
∴平行四边形有:□ABCD,□AEOF, □GOFD, □BEOH, □CHOG.
学生2回答:
还有平行四边形:□AEGD, □BEGC. □ABHF, □CHFD.
教师提示:
用定义判定平行四边形,即看四边形两组对边是否分别平行.
出示课件8,学生自主练习后口答,教师订正.
2.出示课件9-12,探究平行四边形边的特征
教师问:平行四边形除两组对边分别平行外,你还能得到对边有什么关系
学生回答:看到两组对边是相等的.
教师问:用什么方法得到这个关系
学生回答:可以观察一下,看到相等.
教师问:观察的准确吗?如何验证呢?
学生回答:利用刻度尺测量一下.
教师问:如何测量呢?
学生回答:测量方法演示见课件(出示课件9)
教师问:度量的结果准确吗?
学生回答:容易有误差.
教师问:有什么方法更简单准确呢?
学生回答:可以剪裁,折叠看是否重合.(出示课件10)
教师问:剪裁对操作的要求很高,如果操作不当也不准确,有更好的办法吗?
学生回答:推理证明.
教师问:怎样进行证明呢?
师生共同讨论后解答如下:先根据题目画图,再写“已知”与“求证”,最后证明.
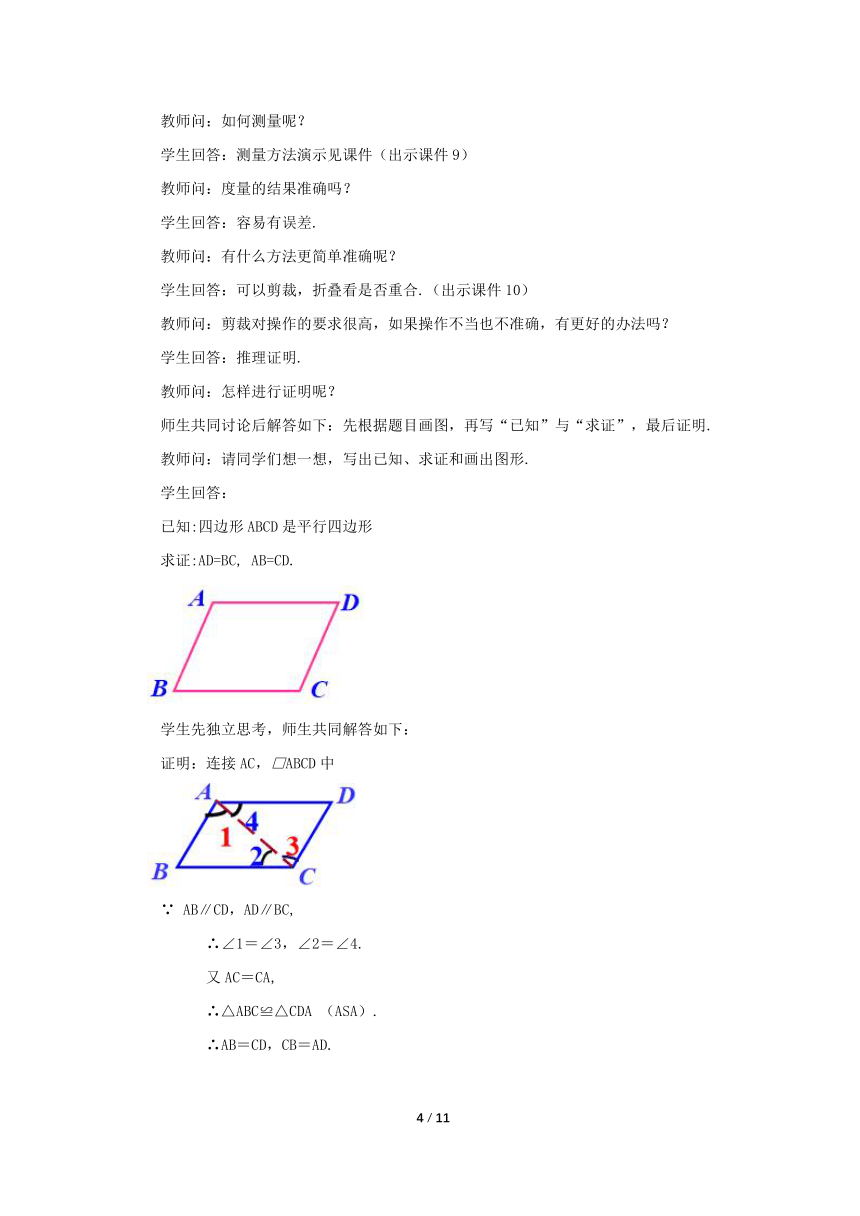
教师问:请同学们想一想,写出已知、求证和画出图形.
学生回答:
已知:四边形ABCD是平行四边形
求证:AD=BC, AB=CD.
学生先独立思考,师生共同解答如下:
证明:连接AC,□ABCD中
∵ AB∥CD,AD∥BC,
∴∠1=∠3,∠2=∠4.
又AC=CA,
∴△ABC≌△CDA (ASA).
∴AB=CD,CB=AD.
总结点拨:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.
总结归纳:(出示课件12)
平行四边形的性质
平行四边形的两组对边分别相等.
教师问:你能利用几何语言描述一下吗?
师生总结:
几何语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC(平行四边形的对边相等).
或
在□ABCD中,AB=CD,AD=BC(平行四边形的对边相等).
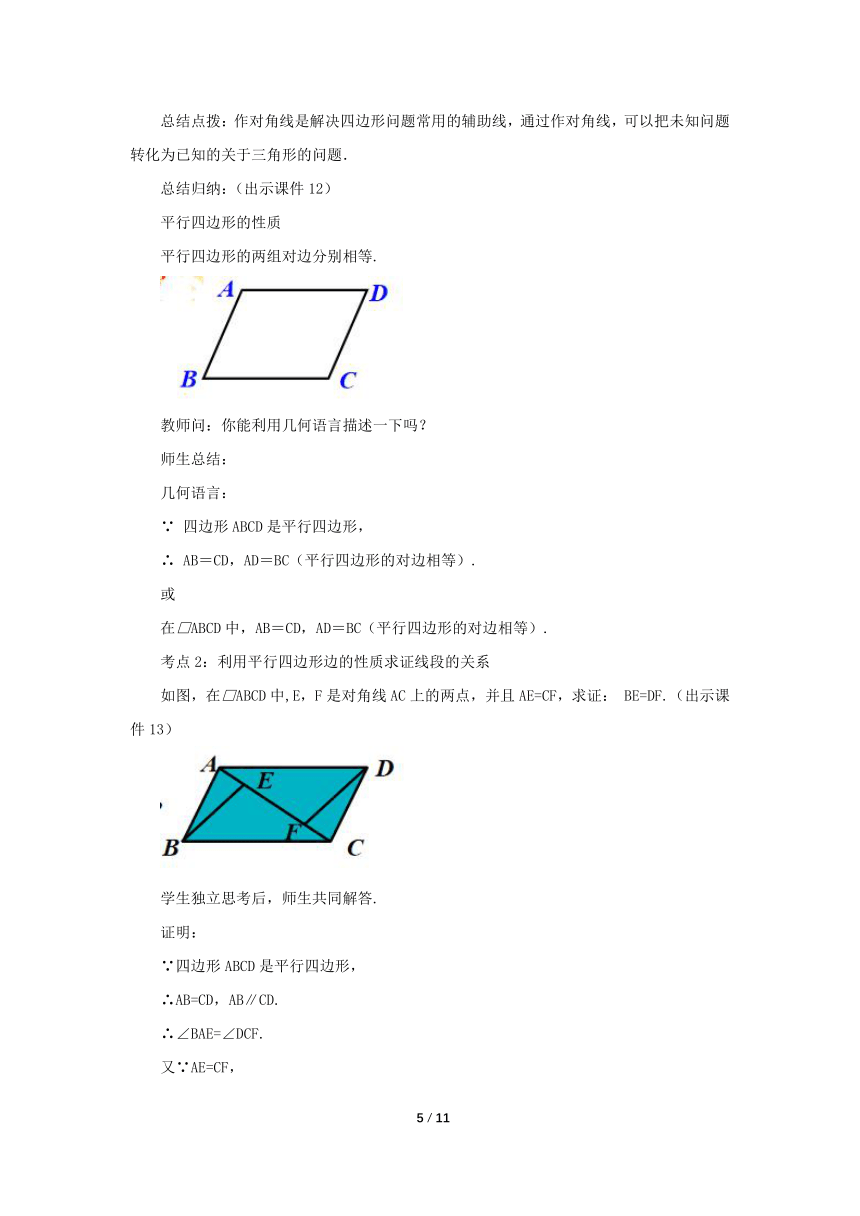
考点2:利用平行四边形边的性质求证线段的关系
如图,在□ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.(出示课件13)
学生独立思考后,师生共同解答.
证明:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又∵AE=CF,
∴△ABE≌△CDF.
∴BE=DF.
出示课件14,学生自主练习后口答,教师订正.
3.出示课件15-18,探究平行四边形角的特征
教师问:前面我们探究了平行四边形的边的性质,平行四边形的角有何性质呢?
学生回答:看着有的相等吧!
教师问:请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与∠D之间的数量关系吗
学生回答:测得∠A =∠C,∠B =∠D.(出示课件15)
教师问:平行四边形的两组对角有什么数量关系?
学生回答:猜想平行四边形的两组对角分别相等.
教师问:怎样证明这个猜想呢?
学生回答:写出已知、求证, 画出图形, 进行证明.
教师问:如何证明呢?
师生共同解答如下:
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA.
∴∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
教师问:不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
学生讨论后解答:
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠A+∠B=180°,∠A+∠D=180°.
∴∠B=∠D.
同理可得∠A=∠C.
总结点拨:(出示课件18)
平行四边形的性质
平行四边形的两组对角分别相等.
教师问:你能利用几何语言描述一下平行四边形角的性质吗?
师生总结如下:
几何语言:
∵ 四边形ABCD是平行四边形,
∴∠A=∠C, ∠B=∠D(平行四边形的对角相等).
或
在□ABCD中,∠A=∠C, ∠B=∠D(平行四边形的对角相等).
考点1:利用平行四边形角的性质求证角的关系
在□ABCD中,已知∠A=52°,求其余三个角的度数.(出示课件19)
学生独立思考后,师生共同解答.
解: ∵四边形ABCD是平行四边形且∠A=52°(已知),
∴∠C=∠A=52°(平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °.
出示课件20,学生自主练习,教师给出答案.
4.出示课件21-23,探究平行线间的距离
教师问:如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.线段AE与CF有怎样的数量关系?
学生回答:AE=CF
教师问:你能写出证明过程吗?
学生回答:
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
∴AE=CF.
教师问:在上述证明中还能得出什么结论?
学生回答:线段DE=BF.
教师问:如果改变条件,还有这样的性质吗?例如:若m // n,作 AB//CD//EF,分别交 m于A,C,E,交 n于B,D,F.
线段AB,CD,EF相等吗?
学生回答:AB=CD=EF
教师问:你是如何得到结果的呢?
学生回答:由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形. 由平行四边形的性质得AB=CD=EF.
师生共同归纳:两条平行线之间的平行线段相等.
教师问:什么是点直线的距离呢?
学生回答:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
教师问:如果点在一条直线上呢?例如下面的问题:
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
师生共同讨论后解答如下:
若m//n,AB , CD , EF垂直于n,交n于B , D , F , 交 m于A , C , E.
学生回答:因为AB , CD , EF垂直于 n,所以∠ABD=∠CDF=∠EFH,所以AB∥CD∥EF,所以四边形ABCD和四边形CDFE都是平行四边形,由此得到AB=CD=EF.
教师问:由上面的证明你得到什么呢?
学生回答:平行线间的距离相等.
教师归纳如下:两条平行线间的距离相等.
出示课件24,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件25-30)
练习课件第25-30页题目,约用时20分钟.
(四)课堂小结(出示课件31)
平行四边形 内 容
定 义 两组对边分别平行的四边形
性 质 1.两组对边分别平行,相等 2.两组对角分别相等,邻角互补
其它结论 1.两条平行线间的距离相等 2.两条平行线间的平行线段也相等
(五)课前预习
预习下节课(18.1.1第2课时)的相关内容.
知道平行四边形的对角线的性质
七、课后作业
教材第43页练习第1,2题.
八、板书设计
第1课时
1.平行四边形的定义
考点1
2.平行四边形边的性质
考点1
3.平行四边形边的性质
考点1
4.平行线间的距离
5.例题讲解
九、教学反思
成功之处:本节以探究活动的形式,让学生通过自主探索、合作交流去发现和体验新知识.整个过程充满着观察、实验、模拟、推断等探索性与挑战性活动.改变了以例题、示范、讲解为主的教学方式,引导学生投入到探索与交流的学习活动中去.这一节课学生已通过画图,测量,猜想的探究方式发现“平行四边形的对边相等,对角相等”等特征.学生参与度高,提高学生的学习兴趣和实际操作能力,取得较好的学习效果.
不足之处:引导学生进行思考的语言不够精练,时间把握得不够好,课堂不够紧凑.由于性质探索部分花了较多时间,导致练习的时间不够多.应该让学生在练习的时候有更多的时间讨论,说得更多.
自我反思:最后的小结部分留足时间,由学生自己归纳本节课的内容,把性质按边、角进行归纳,配以图表方便记忆.补充例题在教学中侧重对学生思路的引导,开阔学生的视野.
1 / 15
第1课时
一、教学目标
【知识与技能】
1.理解平行四边形的定义及有关概念.
2.探究并掌握平行四边形的对边相等、对角相等的性质,利用平行四边形的性质进行简单的计算和证明.
3.了解平行线间距离的概念.
【过程与方法】
1.经历利用平行四边形描述、观察世界的过程,发展学生的形象思维和抽象思维.
2.在进行性质探索的活动过程中,发展学生的探究能力.
3.在性质应用的过程中,提高学生运用数学知识解决实际问题的能力,培养学生的推理能力和逻辑思维能力.
【情感态度与价值观】
在性质应用过程中培养独立思考的习惯,让学生在观察、合作、讨论、交流中感受数学的实际应用价值,同时培养学生善于发现、积极思考、合作学习的学习态度.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
平行四边形边、角的性质探索和证明.
【教学难点】
如何添加辅助线将平行四边形问题转化成三角形问题解决的思想方法.
五、课前准备
教师:课件、三角尺、直尺、教学中出示的教学插图和例题的投影图片等.
学生:三角尺、铅笔、方格纸,量角器,刻度尺.
六、教学过程
(一)导入新课(出示课件2)
我们一起来观察下图中的小区的伸缩门,庭院的竹篱笆等图,它们是什么几何图形
(二)探索新知
1.出示课件4-6,探究平行四边形的定义
教师问:下列常见的四边形它们的边之间有什么关系呢?
师生总结如下:四边形的对边之间有如下关系:
教师问:你们还记得我们以前对平行四边形的定义吗?
学生答:两组对边分别平行的四边形叫做平行四边形.
总结点拨:(出示课件6)
定义:两组对边分别平行的四边形叫做平行四边形.
记作:□ ABCD.
读作:平行四边形ABCD.
判定:
∵AB∥CD, AD∥BC,
∴四边形ABCD是平行四边形.
性质:
∵四边形ABCD是平行四边形,
∴AB∥CD, AD∥BC,
教师强调:图形中字母的标识顺序应为顺时针方向或逆时针方向.
考点1:利用平行四边形的定义判断平行四边形
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.并把它们表示出来.(出示课件7)
师生共同讨论解答如下:
教师依次展示学生答案:
学生1解答:∵DC∥FH ∥ AB,DA∥ EG∥ CB,
∴平行四边形有:□ABCD,□AEOF, □GOFD, □BEOH, □CHOG.
学生2回答:
还有平行四边形:□AEGD, □BEGC. □ABHF, □CHFD.
教师提示:
用定义判定平行四边形,即看四边形两组对边是否分别平行.
出示课件8,学生自主练习后口答,教师订正.
2.出示课件9-12,探究平行四边形边的特征
教师问:平行四边形除两组对边分别平行外,你还能得到对边有什么关系
学生回答:看到两组对边是相等的.
教师问:用什么方法得到这个关系
学生回答:可以观察一下,看到相等.
教师问:观察的准确吗?如何验证呢?
学生回答:利用刻度尺测量一下.
教师问:如何测量呢?
学生回答:测量方法演示见课件(出示课件9)
教师问:度量的结果准确吗?
学生回答:容易有误差.
教师问:有什么方法更简单准确呢?
学生回答:可以剪裁,折叠看是否重合.(出示课件10)
教师问:剪裁对操作的要求很高,如果操作不当也不准确,有更好的办法吗?
学生回答:推理证明.
教师问:怎样进行证明呢?
师生共同讨论后解答如下:先根据题目画图,再写“已知”与“求证”,最后证明.
教师问:请同学们想一想,写出已知、求证和画出图形.
学生回答:
已知:四边形ABCD是平行四边形
求证:AD=BC, AB=CD.
学生先独立思考,师生共同解答如下:
证明:连接AC,□ABCD中
∵ AB∥CD,AD∥BC,
∴∠1=∠3,∠2=∠4.
又AC=CA,
∴△ABC≌△CDA (ASA).
∴AB=CD,CB=AD.
总结点拨:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.
总结归纳:(出示课件12)
平行四边形的性质
平行四边形的两组对边分别相等.
教师问:你能利用几何语言描述一下吗?
师生总结:
几何语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC(平行四边形的对边相等).
或
在□ABCD中,AB=CD,AD=BC(平行四边形的对边相等).
考点2:利用平行四边形边的性质求证线段的关系
如图,在□ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.(出示课件13)
学生独立思考后,师生共同解答.
证明:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又∵AE=CF,
∴△ABE≌△CDF.
∴BE=DF.
出示课件14,学生自主练习后口答,教师订正.
3.出示课件15-18,探究平行四边形角的特征
教师问:前面我们探究了平行四边形的边的性质,平行四边形的角有何性质呢?
学生回答:看着有的相等吧!
教师问:请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与∠D之间的数量关系吗
学生回答:测得∠A =∠C,∠B =∠D.(出示课件15)
教师问:平行四边形的两组对角有什么数量关系?
学生回答:猜想平行四边形的两组对角分别相等.
教师问:怎样证明这个猜想呢?
学生回答:写出已知、求证, 画出图形, 进行证明.
教师问:如何证明呢?
师生共同解答如下:
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA.
∴∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
教师问:不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
学生讨论后解答:
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠A+∠B=180°,∠A+∠D=180°.
∴∠B=∠D.
同理可得∠A=∠C.
总结点拨:(出示课件18)
平行四边形的性质
平行四边形的两组对角分别相等.
教师问:你能利用几何语言描述一下平行四边形角的性质吗?
师生总结如下:
几何语言:
∵ 四边形ABCD是平行四边形,
∴∠A=∠C, ∠B=∠D(平行四边形的对角相等).
或
在□ABCD中,∠A=∠C, ∠B=∠D(平行四边形的对角相等).
考点1:利用平行四边形角的性质求证角的关系
在□ABCD中,已知∠A=52°,求其余三个角的度数.(出示课件19)
学生独立思考后,师生共同解答.
解: ∵四边形ABCD是平行四边形且∠A=52°(已知),
∴∠C=∠A=52°(平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °.
出示课件20,学生自主练习,教师给出答案.
4.出示课件21-23,探究平行线间的距离
教师问:如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.线段AE与CF有怎样的数量关系?
学生回答:AE=CF
教师问:你能写出证明过程吗?
学生回答:
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
∴AE=CF.
教师问:在上述证明中还能得出什么结论?
学生回答:线段DE=BF.
教师问:如果改变条件,还有这样的性质吗?例如:若m // n,作 AB//CD//EF,分别交 m于A,C,E,交 n于B,D,F.
线段AB,CD,EF相等吗?
学生回答:AB=CD=EF
教师问:你是如何得到结果的呢?
学生回答:由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形. 由平行四边形的性质得AB=CD=EF.
师生共同归纳:两条平行线之间的平行线段相等.
教师问:什么是点直线的距离呢?
学生回答:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
教师问:如果点在一条直线上呢?例如下面的问题:
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
师生共同讨论后解答如下:
若m//n,AB , CD , EF垂直于n,交n于B , D , F , 交 m于A , C , E.
学生回答:因为AB , CD , EF垂直于 n,所以∠ABD=∠CDF=∠EFH,所以AB∥CD∥EF,所以四边形ABCD和四边形CDFE都是平行四边形,由此得到AB=CD=EF.
教师问:由上面的证明你得到什么呢?
学生回答:平行线间的距离相等.
教师归纳如下:两条平行线间的距离相等.
出示课件24,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件25-30)
练习课件第25-30页题目,约用时20分钟.
(四)课堂小结(出示课件31)
平行四边形 内 容
定 义 两组对边分别平行的四边形
性 质 1.两组对边分别平行,相等 2.两组对角分别相等,邻角互补
其它结论 1.两条平行线间的距离相等 2.两条平行线间的平行线段也相等
(五)课前预习
预习下节课(18.1.1第2课时)的相关内容.
知道平行四边形的对角线的性质
七、课后作业
教材第43页练习第1,2题.
八、板书设计
第1课时
1.平行四边形的定义
考点1
2.平行四边形边的性质
考点1
3.平行四边形边的性质
考点1
4.平行线间的距离
5.例题讲解
九、教学反思
成功之处:本节以探究活动的形式,让学生通过自主探索、合作交流去发现和体验新知识.整个过程充满着观察、实验、模拟、推断等探索性与挑战性活动.改变了以例题、示范、讲解为主的教学方式,引导学生投入到探索与交流的学习活动中去.这一节课学生已通过画图,测量,猜想的探究方式发现“平行四边形的对边相等,对角相等”等特征.学生参与度高,提高学生的学习兴趣和实际操作能力,取得较好的学习效果.
不足之处:引导学生进行思考的语言不够精练,时间把握得不够好,课堂不够紧凑.由于性质探索部分花了较多时间,导致练习的时间不够多.应该让学生在练习的时候有更多的时间讨论,说得更多.
自我反思:最后的小结部分留足时间,由学生自己归纳本节课的内容,把性质按边、角进行归纳,配以图表方便记忆.补充例题在教学中侧重对学生思路的引导,开阔学生的视野.
1 / 15
