人教版八年级数学下册 18.2.1 矩形(第1课时)教案
文档属性
| 名称 | 人教版八年级数学下册 18.2.1 矩形(第1课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 22:05:51 | ||
图片预览



文档简介
18.2 .1 矩形
第1课时
一、教学目标
【知识与技能】
1.认识矩形,理解并运用矩形的性质定理计算或证明.
2.掌握直角三角形斜边上的中线等于斜边的一半,会用它解决求线段长或线段倍分关系的问题.
【过程与方法】
让学生经历探索矩形的性质定理和判定定理、直角三角形性质的过程,进一步获得对图形的探索、猜测和证明的经验,发展推理能力.
【情感态度与价值观】
1.通过探究矩形与平行四边形的区别与联系,使学生体会一般与特殊的关系.
2.通过课堂活动培养学生观察、归纳、猜想、证明的探索精神和实践能力,发展学生的合情推理能力,进一步培养学生的逻辑思维能力、推理论证能力及表达能力.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
矩形性质定理的运用.
【教学难点】
利用矩形的性质定理进行证明和计算.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本、直尺、量角器、橡皮擦、课本、铅笔盒.
六、教学过程
(一)导入新课(出示课件2)
我们都知道三角形具有稳定性,平行四边形是否也具有稳定性?
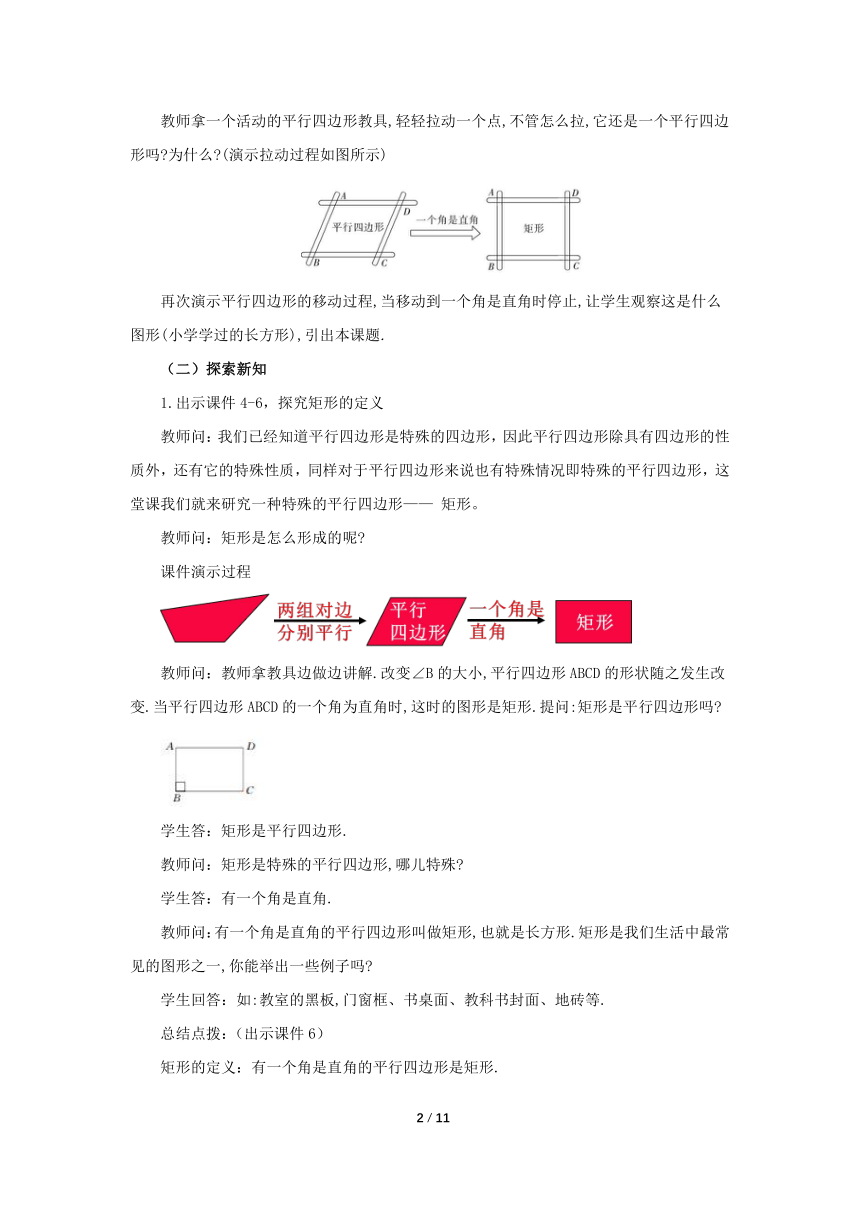
教师拿一个活动的平行四边形教具,轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗 为什么 (演示拉动过程如图所示)
再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形(小学学过的长方形),引出本课题.
(二)探索新知
1.出示课件4-6,探究矩形的定义
教师问:我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况即特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形—— 矩形。
教师问:矩形是怎么形成的呢
课件演示过程
教师问:教师拿教具边做边讲解.改变∠B的大小,平行四边形ABCD的形状随之发生改变.当平行四边形ABCD的一个角为直角时,这时的图形是矩形.提问:矩形是平行四边形吗
学生答:矩形是平行四边形.
教师问:矩形是特殊的平行四边形,哪儿特殊
学生答:有一个角是直角.
教师问:有一个角是直角的平行四边形叫做矩形,也就是长方形.矩形是我们生活中最常见的图形之一,你能举出一些例子吗
学生回答:如:教室的黑板,门窗框、书桌面、教科书封面、地砖等.
总结点拨:(出示课件6)
矩形的定义:有一个角是直角的平行四边形是矩形.
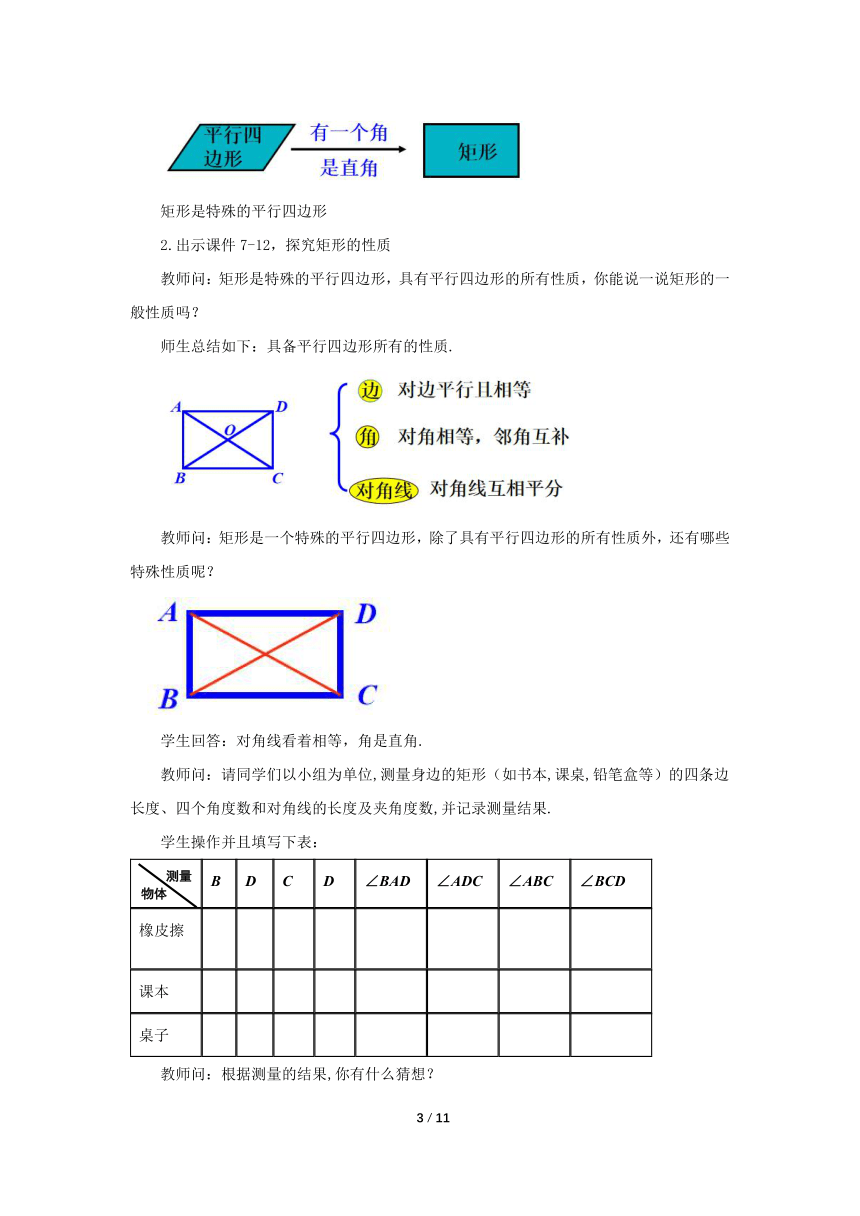
矩形是特殊的平行四边形
2.出示课件7-12,探究矩形的性质
教师问:矩形是特殊的平行四边形,具有平行四边形的所有性质,你能说一说矩形的一般性质吗?
师生总结如下:具备平行四边形所有的性质.
教师问:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
学生回答:对角线看着相等,角是直角.
教师问:请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
学生操作并且填写下表:
B D C D ∠BAD ∠ADC ∠ABC ∠BCD
橡皮擦
课本
桌子
教师问:根据测量的结果,你有什么猜想?
学生1回答:矩形的四个角都是直角.
学生2回答:矩形的对角线相等.
教师问:怎么证明猜想1呢?
师生一起解答:
求证:矩形的四个角都是直角.
已知:如图所示,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵四边形ABCD是矩形,
∴ ∠A=90°.
又∵ 矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
教师问:猜想2又怎么证明呢?
师生一起解答:
求证:矩形的对角线相等
已知:如图,四边形ABCD是矩形. 求证:AC = BD.
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB (SAS).
∴AC = BD,
即矩形的对角线相等.
总结点拨:(出示课件13)
矩形特殊的性质:
从角上看:矩形的四个角都是直角.
从对角线上看:
矩形的两条对角线相等.
归纳总结:(出示课件14)
矩形的性质:
边:矩形的两组对边分别平行;矩形的两组对边分别相等.
角:矩形的四个角都是直角
对角线:矩形的两条对角线相等;矩形的两条对角线互相平分.
数学语言:
∵四边形ABCD是矩形,
∴AD∥BC,CD∥AB.
∴AD=BC,CD=AB.
∴AC=BD.
∴AO=CO,OD=OB.
∴∠A=∠B=∠C=∠D=90°.
考点1:利用矩形的性质求线段的长
如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.(出示课件15)
师生共同讨论解答如下:
解:∵四边形ABCD是矩形.
∴AC=BD,
OA=OC=AC,OB=OD=BD ,
∴OA=OB.
又∵∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴AC=BD=2OA=8.
总结点拨:矩形的对角线相等且互相平分.
出示课件16,学生自主练习后口答,教师订正.
考点2:利用矩形的性质解答折叠问题
将矩形纸片ABCD沿对角线BD对折,再折叠使AD与对角线BD重合,得折痕DG,若AB=8,BC=6,求AG的长.(出示课件17)
学生独立思考后,师生共同解答.
解:矩形纸片ABCD中,∠DAB=90°,AD=BC, AB=CD,BD===10.
又∵△ADG沿DG折叠得到△A′DG,
∴△ADG≌△ A′DG.
∴AD=A′D, AG=A′G,A′B=AB-A′D=10-6=4,
设AG=x,则BG=AB-AG=8-x,
在Rt△GA′B中,由勾股定理得,A′B2+A′G2=BG2
∴x2+42=(8-x)2 解得x=3.
∴ AG=3.
总结点拨:(出示课件17)
在矩形中,常遇到折叠问题,利用勾股定理列方程是解决问题的基本方法.
出示课件18,学生自主练习后口答,教师订正.
3.出示课件19-23,探究矩形的对称性及相关性质
教师问:矩形ABCD是轴对称图形吗?
学生回答:是轴对称图形.
教师问:矩形ABCD的对称轴有几条?
学生回答:有2条.
教师问:矩形是中心对称图形吗?
学生回答:是.
教师问:矩形的对称中心是什么?
学生回答:它的对角线的交点.
总结点拨:(出示课件19)
矩形的性质:
对称性:轴对称图形.
对称轴:2条.
中心对称:中心对称图形.对称中心:对角线的交点.
归纳总结:(出示课件20)
边 角 对角线 对称性
平行四边形 对边平行且相等 对角相等 邻角互补 对角线互相平分 中心对称图形
矩形 对边平行且相等 四个角为直角 对角线互相平分且相等 中心对称图形 轴对称图形
教师问:你在矩形中还发现了哪些基本图形?
学生回答:两对全等的等腰三角形.
教师问:还有哪些性质呢?
学生回答:四个全等的直角三角形.
4.出示课件23,探究直角三角形的性质
教师问:如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论?
学生回答:得到一个直角三角形.
教师问:Rt△ABC中,点O是线段AC上的什么点呢?
学生回答:点O是线段AC的中点.
教师问:Rt△ABC中,BO是一条怎样的线段?
学生回答:BO是△ABC的一条中线.
教师问:BO的长度与斜边AC有什么关系?
学生回答:猜想BO的长度等于斜边AC长度的一半.
教师问:你能证明你的猜想吗?
师生共同解答如下:
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO=AC.
证明:延长BO至D, 使OD=BO,连接AD,DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
∴BO=BD=AC.
总结点拨:直角三角形斜边上的中线等于斜边的一半.
考点1:利用直角三角形的性质解答题目
如图,在△ABC中,AD是高,E,F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;(出示课件25)
(2)求证:EF垂直平分AD.(出示课件26)
学生独立思考后,师生共同解答.
解:(1)∵AD是△ABC的高,E,F分别是AB,AC的中点,
∴DE=AE=AB=×10=5,
DF=AF= AC=×8=4.
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴E,F在线段AD的垂直平分线上.
∴EF垂直平分AD.
师生共同归纳:当已知条件含有线段的中点、直角三角形的条件时,可联想直角三角形斜边上的中线的性质进行求解.
出示课件27,学生自主练习,教师给出答案。
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件28-34)
练习课件第28-34页题目,约用时20分钟.
(四)课堂小结(出示课件35)
内 容
矩形的概念 有一个角是直角的平行四边形叫做矩形
矩形的性质 1.具有平行四边形的一切性质; 2.四个内角都是直角,两条对角线互相平分且相等 3.具有2条对称轴的轴对称图形
直角三角形的性质 直角三角形斜边上的中线等于斜边的一半
(五)课前预习
预习下节课(18.2.1第2课时)的相关内容.
知道矩形的判定定理1和判定定理2.
七、课后作业
教材第53页练习第1,2,3题.
八、板书设计
矩形
第1课时
1.矩形的定义
2.矩形的性质
考点1 考点2
3.矩形的对称性及相关性质
4.直角三角形性质
考点1
5.考点讲解
九、教学反思
成功之处:本节课内容是矩形的性质,本课按矩形的定义——矩形的性质(一般性质和特殊性质)——矩形性质与平行四边形性质的比较的流程进行讲解.整节课目标明确,让学生清楚地意识到这节课需要掌握的知识;内容比较流畅,知识点很自然地串联在一起;课堂目标完成良好,学生的反应力和做题的正确率都比较好.
不足之处:知识的掌握需要有一个内化的过程,不可能一蹴而就,由于课堂时间有限,加上学生个体的差异,有部分学生不能灵活运用所学来解决相关的问题.
补救措施:在教学方案的实施上,要想方设法调动学生学习的积极性,尽量发挥学生的主体作用,团队作用.
1 / 14
第1课时
一、教学目标
【知识与技能】
1.认识矩形,理解并运用矩形的性质定理计算或证明.
2.掌握直角三角形斜边上的中线等于斜边的一半,会用它解决求线段长或线段倍分关系的问题.
【过程与方法】
让学生经历探索矩形的性质定理和判定定理、直角三角形性质的过程,进一步获得对图形的探索、猜测和证明的经验,发展推理能力.
【情感态度与价值观】
1.通过探究矩形与平行四边形的区别与联系,使学生体会一般与特殊的关系.
2.通过课堂活动培养学生观察、归纳、猜想、证明的探索精神和实践能力,发展学生的合情推理能力,进一步培养学生的逻辑思维能力、推理论证能力及表达能力.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
矩形性质定理的运用.
【教学难点】
利用矩形的性质定理进行证明和计算.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔、练习本、直尺、量角器、橡皮擦、课本、铅笔盒.
六、教学过程
(一)导入新课(出示课件2)
我们都知道三角形具有稳定性,平行四边形是否也具有稳定性?
教师拿一个活动的平行四边形教具,轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗 为什么 (演示拉动过程如图所示)
再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形(小学学过的长方形),引出本课题.
(二)探索新知
1.出示课件4-6,探究矩形的定义
教师问:我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况即特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形—— 矩形。
教师问:矩形是怎么形成的呢
课件演示过程
教师问:教师拿教具边做边讲解.改变∠B的大小,平行四边形ABCD的形状随之发生改变.当平行四边形ABCD的一个角为直角时,这时的图形是矩形.提问:矩形是平行四边形吗
学生答:矩形是平行四边形.
教师问:矩形是特殊的平行四边形,哪儿特殊
学生答:有一个角是直角.
教师问:有一个角是直角的平行四边形叫做矩形,也就是长方形.矩形是我们生活中最常见的图形之一,你能举出一些例子吗
学生回答:如:教室的黑板,门窗框、书桌面、教科书封面、地砖等.
总结点拨:(出示课件6)
矩形的定义:有一个角是直角的平行四边形是矩形.
矩形是特殊的平行四边形
2.出示课件7-12,探究矩形的性质
教师问:矩形是特殊的平行四边形,具有平行四边形的所有性质,你能说一说矩形的一般性质吗?
师生总结如下:具备平行四边形所有的性质.
教师问:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
学生回答:对角线看着相等,角是直角.
教师问:请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
学生操作并且填写下表:
B D C D ∠BAD ∠ADC ∠ABC ∠BCD
橡皮擦
课本
桌子
教师问:根据测量的结果,你有什么猜想?
学生1回答:矩形的四个角都是直角.
学生2回答:矩形的对角线相等.
教师问:怎么证明猜想1呢?
师生一起解答:
求证:矩形的四个角都是直角.
已知:如图所示,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵四边形ABCD是矩形,
∴ ∠A=90°.
又∵ 矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
教师问:猜想2又怎么证明呢?
师生一起解答:
求证:矩形的对角线相等
已知:如图,四边形ABCD是矩形. 求证:AC = BD.
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB (SAS).
∴AC = BD,
即矩形的对角线相等.
总结点拨:(出示课件13)
矩形特殊的性质:
从角上看:矩形的四个角都是直角.
从对角线上看:
矩形的两条对角线相等.
归纳总结:(出示课件14)
矩形的性质:
边:矩形的两组对边分别平行;矩形的两组对边分别相等.
角:矩形的四个角都是直角
对角线:矩形的两条对角线相等;矩形的两条对角线互相平分.
数学语言:
∵四边形ABCD是矩形,
∴AD∥BC,CD∥AB.
∴AD=BC,CD=AB.
∴AC=BD.
∴AO=CO,OD=OB.
∴∠A=∠B=∠C=∠D=90°.
考点1:利用矩形的性质求线段的长
如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.(出示课件15)
师生共同讨论解答如下:
解:∵四边形ABCD是矩形.
∴AC=BD,
OA=OC=AC,OB=OD=BD ,
∴OA=OB.
又∵∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴AC=BD=2OA=8.
总结点拨:矩形的对角线相等且互相平分.
出示课件16,学生自主练习后口答,教师订正.
考点2:利用矩形的性质解答折叠问题
将矩形纸片ABCD沿对角线BD对折,再折叠使AD与对角线BD重合,得折痕DG,若AB=8,BC=6,求AG的长.(出示课件17)
学生独立思考后,师生共同解答.
解:矩形纸片ABCD中,∠DAB=90°,AD=BC, AB=CD,BD===10.
又∵△ADG沿DG折叠得到△A′DG,
∴△ADG≌△ A′DG.
∴AD=A′D, AG=A′G,A′B=AB-A′D=10-6=4,
设AG=x,则BG=AB-AG=8-x,
在Rt△GA′B中,由勾股定理得,A′B2+A′G2=BG2
∴x2+42=(8-x)2 解得x=3.
∴ AG=3.
总结点拨:(出示课件17)
在矩形中,常遇到折叠问题,利用勾股定理列方程是解决问题的基本方法.
出示课件18,学生自主练习后口答,教师订正.
3.出示课件19-23,探究矩形的对称性及相关性质
教师问:矩形ABCD是轴对称图形吗?
学生回答:是轴对称图形.
教师问:矩形ABCD的对称轴有几条?
学生回答:有2条.
教师问:矩形是中心对称图形吗?
学生回答:是.
教师问:矩形的对称中心是什么?
学生回答:它的对角线的交点.
总结点拨:(出示课件19)
矩形的性质:
对称性:轴对称图形.
对称轴:2条.
中心对称:中心对称图形.对称中心:对角线的交点.
归纳总结:(出示课件20)
边 角 对角线 对称性
平行四边形 对边平行且相等 对角相等 邻角互补 对角线互相平分 中心对称图形
矩形 对边平行且相等 四个角为直角 对角线互相平分且相等 中心对称图形 轴对称图形
教师问:你在矩形中还发现了哪些基本图形?
学生回答:两对全等的等腰三角形.
教师问:还有哪些性质呢?
学生回答:四个全等的直角三角形.
4.出示课件23,探究直角三角形的性质
教师问:如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论?
学生回答:得到一个直角三角形.
教师问:Rt△ABC中,点O是线段AC上的什么点呢?
学生回答:点O是线段AC的中点.
教师问:Rt△ABC中,BO是一条怎样的线段?
学生回答:BO是△ABC的一条中线.
教师问:BO的长度与斜边AC有什么关系?
学生回答:猜想BO的长度等于斜边AC长度的一半.
教师问:你能证明你的猜想吗?
师生共同解答如下:
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO=AC.
证明:延长BO至D, 使OD=BO,连接AD,DC.
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
∴BO=BD=AC.
总结点拨:直角三角形斜边上的中线等于斜边的一半.
考点1:利用直角三角形的性质解答题目
如图,在△ABC中,AD是高,E,F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;(出示课件25)
(2)求证:EF垂直平分AD.(出示课件26)
学生独立思考后,师生共同解答.
解:(1)∵AD是△ABC的高,E,F分别是AB,AC的中点,
∴DE=AE=AB=×10=5,
DF=AF= AC=×8=4.
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴E,F在线段AD的垂直平分线上.
∴EF垂直平分AD.
师生共同归纳:当已知条件含有线段的中点、直角三角形的条件时,可联想直角三角形斜边上的中线的性质进行求解.
出示课件27,学生自主练习,教师给出答案。
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧。
(三)课堂练习(出示课件28-34)
练习课件第28-34页题目,约用时20分钟.
(四)课堂小结(出示课件35)
内 容
矩形的概念 有一个角是直角的平行四边形叫做矩形
矩形的性质 1.具有平行四边形的一切性质; 2.四个内角都是直角,两条对角线互相平分且相等 3.具有2条对称轴的轴对称图形
直角三角形的性质 直角三角形斜边上的中线等于斜边的一半
(五)课前预习
预习下节课(18.2.1第2课时)的相关内容.
知道矩形的判定定理1和判定定理2.
七、课后作业
教材第53页练习第1,2,3题.
八、板书设计
矩形
第1课时
1.矩形的定义
2.矩形的性质
考点1 考点2
3.矩形的对称性及相关性质
4.直角三角形性质
考点1
5.考点讲解
九、教学反思
成功之处:本节课内容是矩形的性质,本课按矩形的定义——矩形的性质(一般性质和特殊性质)——矩形性质与平行四边形性质的比较的流程进行讲解.整节课目标明确,让学生清楚地意识到这节课需要掌握的知识;内容比较流畅,知识点很自然地串联在一起;课堂目标完成良好,学生的反应力和做题的正确率都比较好.
不足之处:知识的掌握需要有一个内化的过程,不可能一蹴而就,由于课堂时间有限,加上学生个体的差异,有部分学生不能灵活运用所学来解决相关的问题.
补救措施:在教学方案的实施上,要想方设法调动学生学习的积极性,尽量发挥学生的主体作用,团队作用.
1 / 14
