人教版八年级数学下册 18.2.3 正方形(第1课时)教案
文档属性
| 名称 | 人教版八年级数学下册 18.2.3 正方形(第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览


文档简介
18.2 .3 正方形
第1课时
一、教学目标
【知识与技能】
1.理解并运用正方形的定义计算和证明.
2.理解并运用正方形的性质进行计算和证明.
3.体会正方形与平行四边形、矩形、菱形的区别与联系,理解一般与特殊的关系.
【过程与方法】
经历正方形的定义及其性质定理的探究过程,丰富认识图形的经验,进一步发展学生的逻辑推理能力和表达能力.
【情感态度与价值观】
让学生在发现、归纳、概括中逐步提高思维能力,培养用数学的思想和方法来思考和分析问题的习惯.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
正方形的定义和性质定理的应用
【教学难点】
正方形与平行四边形、矩形、菱形的区别与联系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔.
六、教学过程
(一)导入新课(出示课件2)
除了矩形和菱形外,还有什么特殊的平行四边形呢?
怎样研究这类图形?想一想我们是怎样研究矩形和菱形的.
(二)探索新知
1.出示课件4-19,探究正方形的定义
学生观看正方形课件演示过程
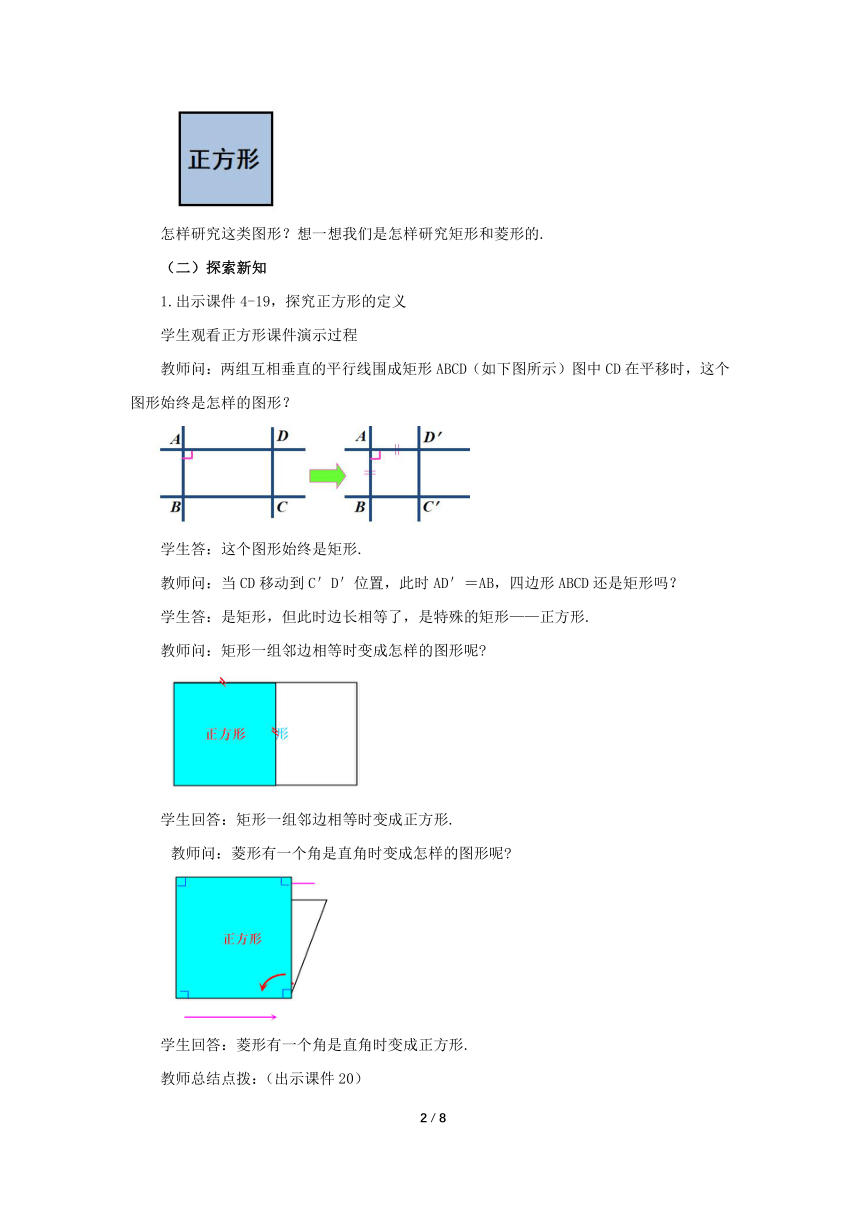
教师问:两组互相垂直的平行线围成矩形ABCD(如下图所示)图中CD在平移时,这个图形始终是怎样的图形?
学生答:这个图形始终是矩形.
教师问:当CD移动到C'D'位置,此时AD'=AB,四边形ABCD还是矩形吗?
学生答:是矩形,但此时边长相等了,是特殊的矩形——正方形.
教师问:矩形一组邻边相等时变成怎样的图形呢
学生回答:矩形一组邻边相等时变成正方形.
教师问:菱形有一个角是直角时变成怎样的图形呢
学生回答:菱形有一个角是直角时变成正方形.
教师总结点拨:(出示课件20)
教师问:如何来给正方形下定义?
学生回答:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.出示课件21-23,探究正方形的性质
教师问:请同学们拿出准备好的正方形纸片,折一折,观察并思考.正方形是不是轴对称图形
学生回答:是轴对称图形.
教师问:有几条对称轴呢
学生回答:有4条对称轴.
教师问:请你说出平行四边形、矩形、菱形、正方形的对称性吗?
学生1回答:平行四边形是中心对称图形,对角线的交点是对称中心.
学生2回答:矩形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有两条对称轴.
学生3回答:菱形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有两条对称轴.
学生4回答:正方形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有四条对称轴.
教师总结点拨:(出示课件22)
平行四边形、矩形、菱形、正方形的对称性
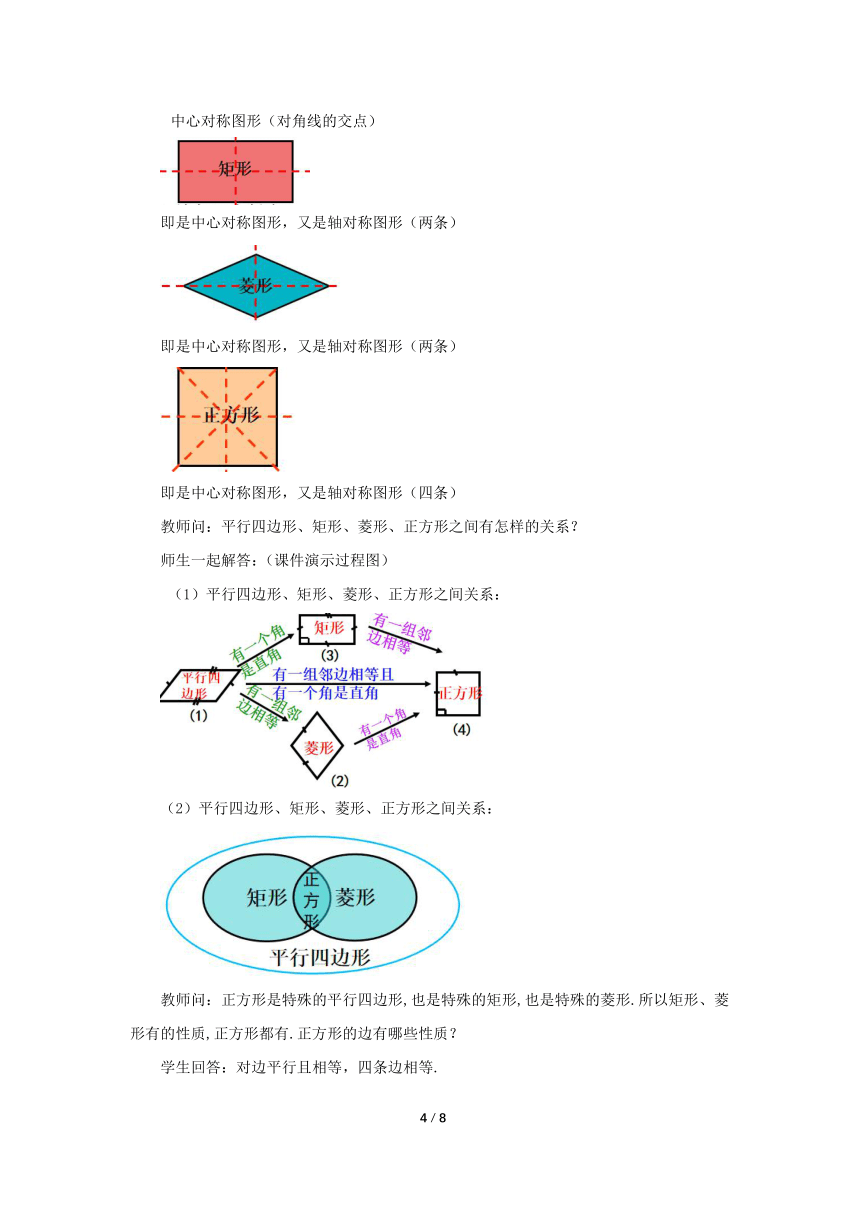
中心对称图形(对角线的交点)
即是中心对称图形,又是轴对称图形(两条)
即是中心对称图形,又是轴对称图形(两条)
即是中心对称图形,又是轴对称图形(四条)
教师问:平行四边形、矩形、菱形、正方形之间有怎样的关系?
师生一起解答:(课件演示过程图)
(1)平行四边形、矩形、菱形、正方形之间关系:
(2)平行四边形、矩形、菱形、正方形之间关系:
教师问:正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.正方形的边有哪些性质?
学生回答:对边平行且相等,四条边相等.
教师问:正方形的角有哪些性质?
学生回答:正方形的四个角都是直角,对角相等,邻角互补.
教师问:正方形的对角线有哪些性质?
学生回答:正方形的对角线相等且互相垂直平分.
总结归纳:
性质:
1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
教师问:试着证明正方形的性质:“正方形的四个角都是直角,四条边相等.”。
师生一起解答:
已知:如图,四边形ABCD是正方形.求证:正方形ABCD四边都相等,四个角都是直角.
证明:
∵四边形ABCD是正方形.
∴∠A=90°, AB=BC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义), 正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
教师问:试证明正方形的性质:“正方形的对角线相等且互相垂直平分.”
师生一起解答:
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
考点1:利用正方形的性质求线段相等
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.求证:△ABO、△BCO、△CDO、 △DAO是全等的等腰直角三角形.
(出示课件27)
师生共同讨论解答如下:
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且
△ABO≌ △BCO≌△CDO≌△DAO.
出示课件28,学生自主练习后口答,教师订正.
考点2:利用正方形的性质求角度
如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.(出示课件29)
学生独立思考后,师生共同解答.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
出示课件30,学生自主练习后口答,教师订正.
考点3:利用正方形的性质证明线段相等
如图四边形ABCD和DEFG都是正方形,试说明AE=CG.(出示课件31)
学生独立思考后,师生共同解答.
解:∵四边形ABCD是正方形,
∴AD=CD.
又∵四边形DEFG也是正方形,
∴DE=DG.
又∵正方形的每个内角为90°,
∴∠ADE+∠EDC=∠CDG+∠EDC,
∴∠ADE=∠CDG.
∴△AED≌△CGD(SAS).
∴AE=CG.
出示课件32,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件33-39)
练习课件第33-39页题目,约用时20分钟.
(四)课堂小结(出示课件40)
内 容
正方形的性质 定义:有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
性质: 1.四个角都是直角 2.四条边都相等 3.对角线相等且互相垂直平分
(五)课前预习
预习下节课(18.2.3第2课时)的相关内容.
知道正方形的判定方法.
七、课后作业
教材第62页习题18.2第15,17题.
八、板书设计
18.2.3 正方形
第1课时
1.正方形的定义
2.正方形的性质
考点1 考点2 考点3
3.例题讲解
九、教学反思
成功之处:通过本节课的教学活动,学生进一步认识了正方形,基本掌握了正方形的定义和性质,并能运用所学的知识解决一些问题.
不足之处:由于课堂时间有限,加上学生个体的差异,学生不能灵活运用所学来解决相关的问题.
自我反思:在课堂教学中,要注意发挥学生的主体作用,团队作用,让学生通过独立思考,合作交流等方式,积极参与到课堂的教学活动中,真正做课堂的主人,学习的主人.
1 / 11
第1课时
一、教学目标
【知识与技能】
1.理解并运用正方形的定义计算和证明.
2.理解并运用正方形的性质进行计算和证明.
3.体会正方形与平行四边形、矩形、菱形的区别与联系,理解一般与特殊的关系.
【过程与方法】
经历正方形的定义及其性质定理的探究过程,丰富认识图形的经验,进一步发展学生的逻辑推理能力和表达能力.
【情感态度与价值观】
让学生在发现、归纳、概括中逐步提高思维能力,培养用数学的思想和方法来思考和分析问题的习惯.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
正方形的定义和性质定理的应用
【教学难点】
正方形与平行四边形、矩形、菱形的区别与联系.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、铅笔.
六、教学过程
(一)导入新课(出示课件2)
除了矩形和菱形外,还有什么特殊的平行四边形呢?
怎样研究这类图形?想一想我们是怎样研究矩形和菱形的.
(二)探索新知
1.出示课件4-19,探究正方形的定义
学生观看正方形课件演示过程
教师问:两组互相垂直的平行线围成矩形ABCD(如下图所示)图中CD在平移时,这个图形始终是怎样的图形?
学生答:这个图形始终是矩形.
教师问:当CD移动到C'D'位置,此时AD'=AB,四边形ABCD还是矩形吗?
学生答:是矩形,但此时边长相等了,是特殊的矩形——正方形.
教师问:矩形一组邻边相等时变成怎样的图形呢
学生回答:矩形一组邻边相等时变成正方形.
教师问:菱形有一个角是直角时变成怎样的图形呢
学生回答:菱形有一个角是直角时变成正方形.
教师总结点拨:(出示课件20)
教师问:如何来给正方形下定义?
学生回答:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.出示课件21-23,探究正方形的性质
教师问:请同学们拿出准备好的正方形纸片,折一折,观察并思考.正方形是不是轴对称图形
学生回答:是轴对称图形.
教师问:有几条对称轴呢
学生回答:有4条对称轴.
教师问:请你说出平行四边形、矩形、菱形、正方形的对称性吗?
学生1回答:平行四边形是中心对称图形,对角线的交点是对称中心.
学生2回答:矩形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有两条对称轴.
学生3回答:菱形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有两条对称轴.
学生4回答:正方形即是中心对称图形,又是轴对称图形,对角线的交点是对称中心,有四条对称轴.
教师总结点拨:(出示课件22)
平行四边形、矩形、菱形、正方形的对称性
中心对称图形(对角线的交点)
即是中心对称图形,又是轴对称图形(两条)
即是中心对称图形,又是轴对称图形(两条)
即是中心对称图形,又是轴对称图形(四条)
教师问:平行四边形、矩形、菱形、正方形之间有怎样的关系?
师生一起解答:(课件演示过程图)
(1)平行四边形、矩形、菱形、正方形之间关系:
(2)平行四边形、矩形、菱形、正方形之间关系:
教师问:正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.正方形的边有哪些性质?
学生回答:对边平行且相等,四条边相等.
教师问:正方形的角有哪些性质?
学生回答:正方形的四个角都是直角,对角相等,邻角互补.
教师问:正方形的对角线有哪些性质?
学生回答:正方形的对角线相等且互相垂直平分.
总结归纳:
性质:
1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
教师问:试着证明正方形的性质:“正方形的四个角都是直角,四条边相等.”。
师生一起解答:
已知:如图,四边形ABCD是正方形.求证:正方形ABCD四边都相等,四个角都是直角.
证明:
∵四边形ABCD是正方形.
∴∠A=90°, AB=BC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义), 正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
教师问:试证明正方形的性质:“正方形的对角线相等且互相垂直平分.”
师生一起解答:
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
考点1:利用正方形的性质求线段相等
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.求证:△ABO、△BCO、△CDO、 △DAO是全等的等腰直角三角形.
(出示课件27)
师生共同讨论解答如下:
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且
△ABO≌ △BCO≌△CDO≌△DAO.
出示课件28,学生自主练习后口答,教师订正.
考点2:利用正方形的性质求角度
如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.(出示课件29)
学生独立思考后,师生共同解答.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
出示课件30,学生自主练习后口答,教师订正.
考点3:利用正方形的性质证明线段相等
如图四边形ABCD和DEFG都是正方形,试说明AE=CG.(出示课件31)
学生独立思考后,师生共同解答.
解:∵四边形ABCD是正方形,
∴AD=CD.
又∵四边形DEFG也是正方形,
∴DE=DG.
又∵正方形的每个内角为90°,
∴∠ADE+∠EDC=∠CDG+∠EDC,
∴∠ADE=∠CDG.
∴△AED≌△CGD(SAS).
∴AE=CG.
出示课件32,学生自主练习,教师给出答案.
教师:学了前面的知识,接下来做几道练习题看看你掌握的怎么样吧.
(三)课堂练习(出示课件33-39)
练习课件第33-39页题目,约用时20分钟.
(四)课堂小结(出示课件40)
内 容
正方形的性质 定义:有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
性质: 1.四个角都是直角 2.四条边都相等 3.对角线相等且互相垂直平分
(五)课前预习
预习下节课(18.2.3第2课时)的相关内容.
知道正方形的判定方法.
七、课后作业
教材第62页习题18.2第15,17题.
八、板书设计
18.2.3 正方形
第1课时
1.正方形的定义
2.正方形的性质
考点1 考点2 考点3
3.例题讲解
九、教学反思
成功之处:通过本节课的教学活动,学生进一步认识了正方形,基本掌握了正方形的定义和性质,并能运用所学的知识解决一些问题.
不足之处:由于课堂时间有限,加上学生个体的差异,学生不能灵活运用所学来解决相关的问题.
自我反思:在课堂教学中,要注意发挥学生的主体作用,团队作用,让学生通过独立思考,合作交流等方式,积极参与到课堂的教学活动中,真正做课堂的主人,学习的主人.
1 / 11
