鲁教版(五四制)数学七年级下册7.5三元一次方程组 课件(共26张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册7.5三元一次方程组 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 890.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-18 09:28:01 | ||
图片预览








文档简介
(共26张PPT)
1.三元一次方程:含有___个未知数,并且所含未知数
的___的_____都是1的方程.
2.三元一次方程组:共含有___个未知数的___个_____
方程所组成的一组方程.
3.三元一次方程组的解:三元一次方程组中各个方程的_______叫做三元一次方程组的解.
三
项
次数
三
三
一次
公共解
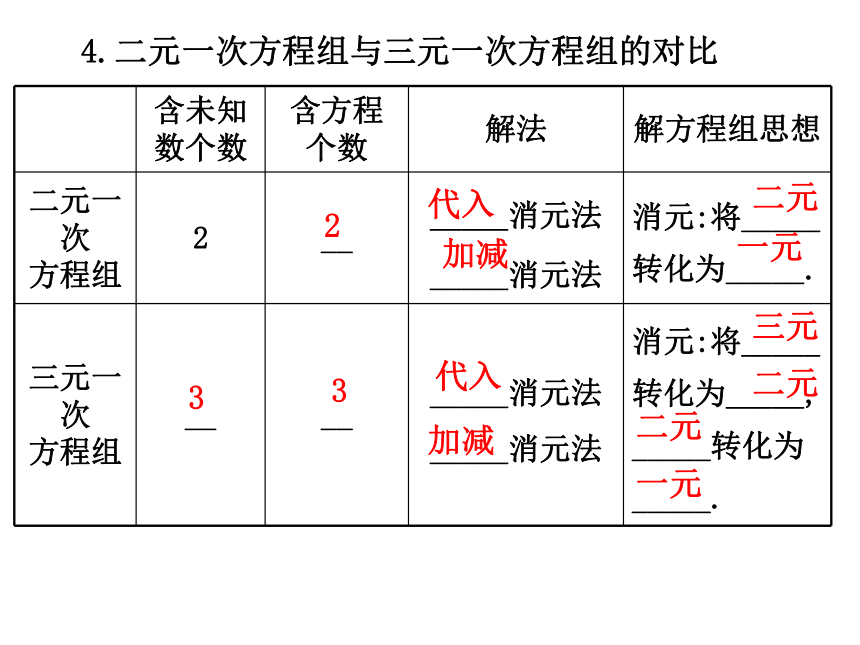
4.二元一次方程组与三元一次方程组的对比
含未知数个数 含方程
个数 解法 解方程组思想
二元一次
方程组 2 __ _____消元法
_____消元法 消元:将_____
转化为_____.
三元一次
方程组 __ __ _____消元法
_____消元法 消元:将_____
转化为_____,
_____转化为
_____.
代入
加减
二元
一元
代入
加减
三元
二元
二元
一元
2
3
3
【思维诊断】(打“√”或“×”)
1.三元一次方程组中的每个方程都含有3个未知数.
( )
2. 不是三元一次方程组. ( )
3.三元一次方程组 的解为
( )
×
×
×
知识与技能:会解简单的三元一次方程组,进一步熟悉解方程组“消元”的基本思想,能针对方程组的特点,选择最好的解法。
过程与方法:培养学生分析能力,能根据题目的特点,确定消元方法、消元对象,培养学生的计算能力、训练解题技巧。
情感、态度、价值观:通过本课的学习,渗透方程恒等变形的数学美以及方程组解的奇异美。
3. 方程组
的解是 .
①-②得y+z=3 ④,
与③联立形成二元一次方程组
③+④得2y=4,解得y=2,把y=2代入④得z=1,
把z=1代入②得x=0,则原方程组的解是
【解析】
三元一次方程组:共含有三个未知数的三个一次方程所组成的一组方程.
思考1:那我们能否先消去y呢?
方程组
的解是 .
①-③得:x+z=1 ④,
与②联立形成二元一次方程组
思考2:那我们能否先消去z呢?
② -③得:x-y=-2 ④
例1.已知等式 y=ax2+bx+c,当x=1时,y=0;当x=2时,y=3;当x=-3时,y=28. (1)求a,b,c的值.
(2)求当x=-1时,y的值。
思考1:这个题有几个条件 如何应用它们?
解:根据题意,得三元一次方程组
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考2:为什么能代入 y=ax2+bx+c呢?
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考3:怎样实现由“三元”转化为“二元” 选择代入法还是加减法
思考4:如果用加减法消元,先消哪个元比较简便
消元,加减消元法
消去c
③-①,得 8a-4b=28 ⑤
④与⑤组成二元一次方程组
3a+b=3,
8a-4b=28.
②-①, 得 3a+b=3
④
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考5:我们需要给④搭配一个什么方程呢?
a=2,
b=-3.
解这个方程组,得
把 代入①,得
a=2,
b=-3
c=1
a=2,
b=-3,
c=1.
因此
(2)当a=2,b=-3,c=1时,
等式y =ax2+bx+c =2x2-3x+1
当x=-1时,y=2×(-1)2-3 ×(-1) +1=6
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
例2:比较下列两个三元一次方程组的异同,寻找合适的方法求解
1、 2、
相同点:都含有两个二元一次方程
不同点:1、所缺少的未知数不同,
2、所缺少的未知数相同。
点拨:两个二元一次方程方程所缺少的未知数不同时,用它们含有的相同未知数y的代数式分別表示另外两个未知数,再将表示这两个未知数的式子代入方程组中第三个方程求解。
1、解:
由①得: ④ 由②得: ⑤
把④、⑤代入③,得:
解此方程得:y=-3,代入④、⑤得,x=2,z=1
所以,原方程组的解为:
2、解:
点拨:方程所缺少的未知数相同时,先直接求解缺少相同未知数的两个方程构成的二元一次方程组,再代入求解。
解①②组成的二元一次方程组
得:
代入③,得:2×(-2)-3 ×(-6)+4z=2
解得:z=4, 所以,原方程组的解为:
1.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
【解析】选D.通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z=25,所以x+y+z=5.
2.解方程组
,则x=_____,y=______,z=_______.
x+y-z=11,
y+z-x=5,
z+x-y=1.
①
②
③
【解析】通过观察未知数的系数,可采取① +②求出y, ②+ ③求出z,最后再将y与z的值代入任何一个方程求出x即可.
答案:6 8 3
3.方程组
【解析】设 ,
所以x=k,y=2k,z=3k,
因为2x-3y+5z=11,
所以2k-6k+15k=11,
所以k=3,
所以x=1,y=2,z=3.
【方法技巧】设第两个方程的比值, 代入第1个方程,
能简单地求出方程组的解.
的解是 .
答案:
1、解三元一次方程组的基本思路是什么
基本方法是什么
2、解三个方程都含有三个未知数的三元一次
方程组时应该注意什么
基本思路:消元
基本方法:代入法和加减法
选择合适的未知数为消去的对象
3、解含有两个二元一次方程的三元一次方程组
① 所缺少的未知数不同时:
用它们含有的相同未知数的代数式分別表示另外两个未知数,再将表示这两个未知数的式子代入方程组中第三个方程求解。
② 所缺少的未知数相同时:
先直接求解缺少相同未知数的两个方程构成的二元一次方程组,再代入求解。
1、抽象概括,去繁取简,体现了类比思想,
2、一般到特殊的转化思想,
3、一题多解,训练了发散思维。
4、学习方法归纳:
1.三元一次方程组 的解为
2.在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
3、用本节课所学的方法解下列三元一次方程:
4. 方程组
的解是 .
1.三元一次方程组 的解为
【解析】
① + ② ,再分别带入①,②,③
答案:
2.在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
【解析】:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2
c=-5
a=3,
b=-2,
c=-5.
因此
答案:a=3,b=-2,c=-5.
3、用本节课所学的方法解下列三元一次方程:
【解析】先判断它属于“解含有两个二元一次方程的
三元一次方程组”的哪种情况?
答案:
4.(2014·海口市第九中学质检)方程组
【解析】因为y∶x=3∶2,y∶z=5∶4,
所以y∶x∶z=15∶10∶12,
设x=10k,y=15k,z=12k,因为x+y+z=111,
所以10k+15k+12k=111,所以k=3,所以x=30,y=45,z=36.
【方法技巧】由后两个方程可求三个未知数的比,通过
设比值代入第1个方程,能简单地求出方程组的解.
的解是 .
答案:
1.三元一次方程:含有___个未知数,并且所含未知数
的___的_____都是1的方程.
2.三元一次方程组:共含有___个未知数的___个_____
方程所组成的一组方程.
3.三元一次方程组的解:三元一次方程组中各个方程的_______叫做三元一次方程组的解.
三
项
次数
三
三
一次
公共解
4.二元一次方程组与三元一次方程组的对比
含未知数个数 含方程
个数 解法 解方程组思想
二元一次
方程组 2 __ _____消元法
_____消元法 消元:将_____
转化为_____.
三元一次
方程组 __ __ _____消元法
_____消元法 消元:将_____
转化为_____,
_____转化为
_____.
代入
加减
二元
一元
代入
加减
三元
二元
二元
一元
2
3
3
【思维诊断】(打“√”或“×”)
1.三元一次方程组中的每个方程都含有3个未知数.
( )
2. 不是三元一次方程组. ( )
3.三元一次方程组 的解为
( )
×
×
×
知识与技能:会解简单的三元一次方程组,进一步熟悉解方程组“消元”的基本思想,能针对方程组的特点,选择最好的解法。
过程与方法:培养学生分析能力,能根据题目的特点,确定消元方法、消元对象,培养学生的计算能力、训练解题技巧。
情感、态度、价值观:通过本课的学习,渗透方程恒等变形的数学美以及方程组解的奇异美。
3. 方程组
的解是 .
①-②得y+z=3 ④,
与③联立形成二元一次方程组
③+④得2y=4,解得y=2,把y=2代入④得z=1,
把z=1代入②得x=0,则原方程组的解是
【解析】
三元一次方程组:共含有三个未知数的三个一次方程所组成的一组方程.
思考1:那我们能否先消去y呢?
方程组
的解是 .
①-③得:x+z=1 ④,
与②联立形成二元一次方程组
思考2:那我们能否先消去z呢?
② -③得:x-y=-2 ④
例1.已知等式 y=ax2+bx+c,当x=1时,y=0;当x=2时,y=3;当x=-3时,y=28. (1)求a,b,c的值.
(2)求当x=-1时,y的值。
思考1:这个题有几个条件 如何应用它们?
解:根据题意,得三元一次方程组
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考2:为什么能代入 y=ax2+bx+c呢?
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考3:怎样实现由“三元”转化为“二元” 选择代入法还是加减法
思考4:如果用加减法消元,先消哪个元比较简便
消元,加减消元法
消去c
③-①,得 8a-4b=28 ⑤
④与⑤组成二元一次方程组
3a+b=3,
8a-4b=28.
②-①, 得 3a+b=3
④
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
思考5:我们需要给④搭配一个什么方程呢?
a=2,
b=-3.
解这个方程组,得
把 代入①,得
a=2,
b=-3
c=1
a=2,
b=-3,
c=1.
因此
(2)当a=2,b=-3,c=1时,
等式y =ax2+bx+c =2x2-3x+1
当x=-1时,y=2×(-1)2-3 ×(-1) +1=6
a+b+c= 0, ①
4a+2b+c=3, ②
9a-3b+c=28. ③
例2:比较下列两个三元一次方程组的异同,寻找合适的方法求解
1、 2、
相同点:都含有两个二元一次方程
不同点:1、所缺少的未知数不同,
2、所缺少的未知数相同。
点拨:两个二元一次方程方程所缺少的未知数不同时,用它们含有的相同未知数y的代数式分別表示另外两个未知数,再将表示这两个未知数的式子代入方程组中第三个方程求解。
1、解:
由①得: ④ 由②得: ⑤
把④、⑤代入③,得:
解此方程得:y=-3,代入④、⑤得,x=2,z=1
所以,原方程组的解为:
2、解:
点拨:方程所缺少的未知数相同时,先直接求解缺少相同未知数的两个方程构成的二元一次方程组,再代入求解。
解①②组成的二元一次方程组
得:
代入③,得:2×(-2)-3 ×(-6)+4z=2
解得:z=4, 所以,原方程组的解为:
1.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为( )
A.2 B.3 C.4 D.5
【解析】选D.通过观察未知数的系数,可采取两个方程相加得,5x+5y+5z=25,所以x+y+z=5.
2.解方程组
,则x=_____,y=______,z=_______.
x+y-z=11,
y+z-x=5,
z+x-y=1.
①
②
③
【解析】通过观察未知数的系数,可采取① +②求出y, ②+ ③求出z,最后再将y与z的值代入任何一个方程求出x即可.
答案:6 8 3
3.方程组
【解析】设 ,
所以x=k,y=2k,z=3k,
因为2x-3y+5z=11,
所以2k-6k+15k=11,
所以k=3,
所以x=1,y=2,z=3.
【方法技巧】设第两个方程的比值, 代入第1个方程,
能简单地求出方程组的解.
的解是 .
答案:
1、解三元一次方程组的基本思路是什么
基本方法是什么
2、解三个方程都含有三个未知数的三元一次
方程组时应该注意什么
基本思路:消元
基本方法:代入法和加减法
选择合适的未知数为消去的对象
3、解含有两个二元一次方程的三元一次方程组
① 所缺少的未知数不同时:
用它们含有的相同未知数的代数式分別表示另外两个未知数,再将表示这两个未知数的式子代入方程组中第三个方程求解。
② 所缺少的未知数相同时:
先直接求解缺少相同未知数的两个方程构成的二元一次方程组,再代入求解。
1、抽象概括,去繁取简,体现了类比思想,
2、一般到特殊的转化思想,
3、一题多解,训练了发散思维。
4、学习方法归纳:
1.三元一次方程组 的解为
2.在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
3、用本节课所学的方法解下列三元一次方程:
4. 方程组
的解是 .
1.三元一次方程组 的解为
【解析】
① + ② ,再分别带入①,②,③
答案:
2.在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
【解析】:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2
c=-5
a=3,
b=-2,
c=-5.
因此
答案:a=3,b=-2,c=-5.
3、用本节课所学的方法解下列三元一次方程:
【解析】先判断它属于“解含有两个二元一次方程的
三元一次方程组”的哪种情况?
答案:
4.(2014·海口市第九中学质检)方程组
【解析】因为y∶x=3∶2,y∶z=5∶4,
所以y∶x∶z=15∶10∶12,
设x=10k,y=15k,z=12k,因为x+y+z=111,
所以10k+15k+12k=111,所以k=3,所以x=30,y=45,z=36.
【方法技巧】由后两个方程可求三个未知数的比,通过
设比值代入第1个方程,能简单地求出方程组的解.
的解是 .
答案:
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
