初中数学九年级下册人教新课标 位似 同步练习
文档属性
| 名称 | 初中数学九年级下册人教新课标 位似 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 190.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-28 11:56:15 | ||
图片预览

文档简介
位似同步练习
一、自主学习
1.位似图形上某一对对应顶点到位中心的距离分别为5 cm和15 cm,则它们的相似比为_________
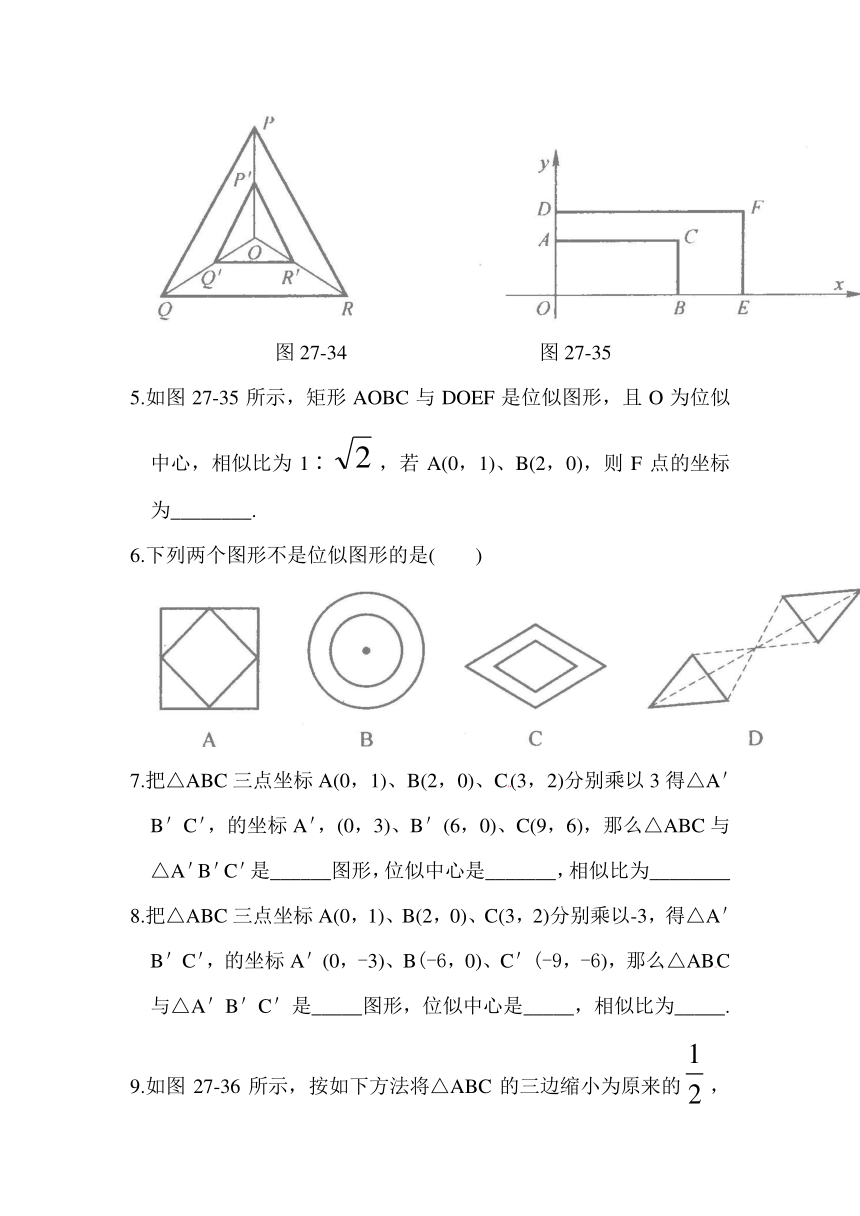
2.如图27-33,蜡烛与成像板之间的距离为3m,小孔纸板距蜡烛1m,若蜡烛AB长20cm,则所成的像长为_________cm.
图27-33
3.四边形ABCD和四边形A'B'C'D'是位似图形,O为位似中心,若OA∶OA',=1∶2,那么AB∶A'B'=________,S四边形ABCD∶S四边形A'B'C'D'=________.
二、基础巩固
4.如图27-34所示,点O是等边△PQR的中心,P,Q',R'分别是OP、OQ、OR的中点,则△P'Q'R'与△PQR是________,点O是_____,相似比是________.
图27-34 图27-35
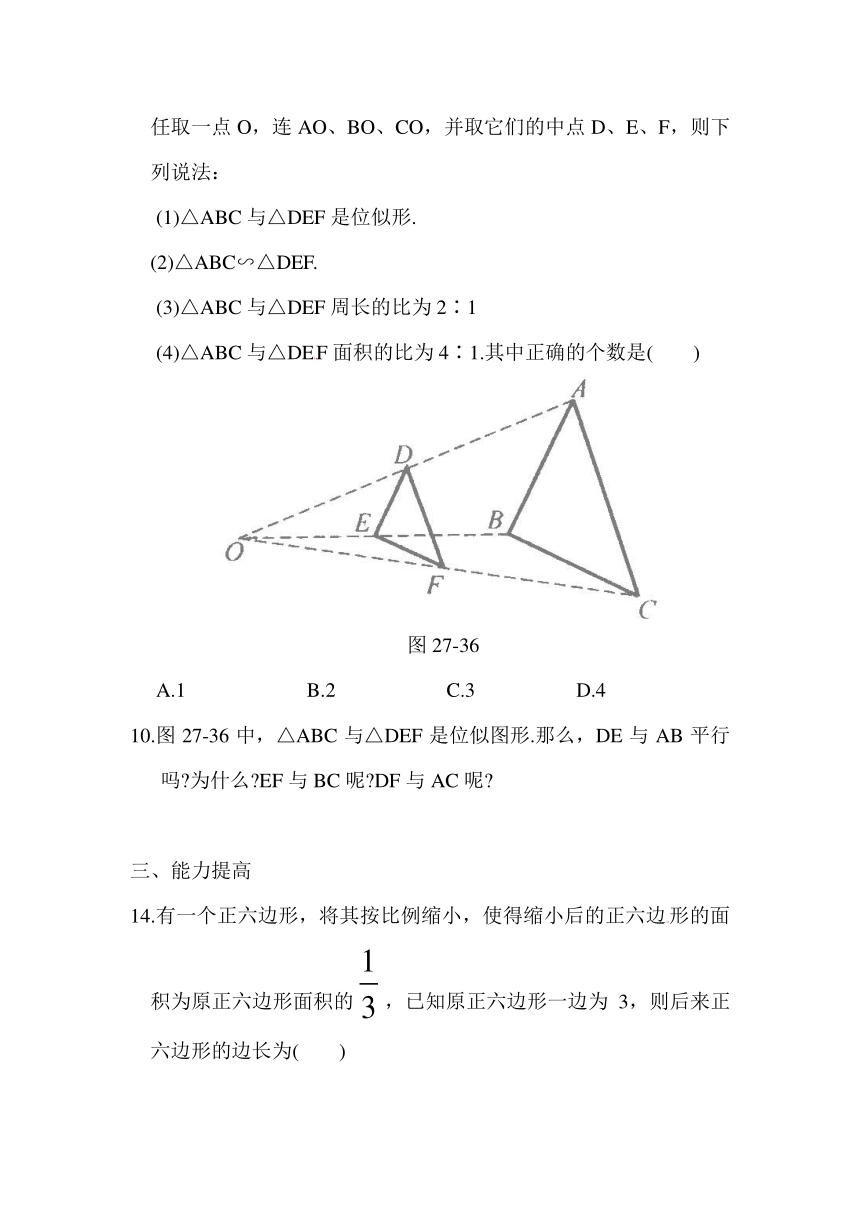
5.如图27-35所示,矩形AOBC与DOEF是位似图形,且O为位似中心,相似比为1∶,若A(0,1)、B(2,0),则F点的坐标为________.
6.下列两个图形不是位似图形的是( )
7.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A'B'C',的坐标A',(0,3)、B'(6,0)、C(9,6),那么△ABC与△A'B'C'是______图形,位似中心是_______,相似比为________
8.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以-3,得△A'B'C',的坐标A'(0,-3)、B(-6,0)、C'(-9,-6),那么△ABC与△A'B'C'是_____图形,位似中心是_____,相似比为_____.
9.如图27-36所示,按如下方法将△ABC的三边缩小为原来的,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,则下列说法:
(1)△ABC与△DEF是位似形.
(2)△ABC∽△DEF.
(3)△ABC与△DEF周长的比为2∶1
(4)△ABC与△DEF面积的比为4∶1.其中正确的个数是( )
图27-36
A.1 B.2 C.3 D.4
10.图27-36中,△ABC与△DEF是位似图形.那么,DE与AB平行吗 为什么 EF与BC呢 DF与AC呢
三、能力提高
14.有一个正六边形,将其按比例缩小,使得缩小后的正六边形的面积为原正六边形面积的,已知原正六边形一边为3,则后来正六边形的边长为( )
A.9 B.3 C. D.
15.在任意一个三角形内部,画一个小三角形,使其各边与原三角形各边平行,则它们的位似中心是( )
A.一定点 B.原三角形三边垂直平分线的交点
C.原三角形角平分线的交点 D.位置不定的一点
16.下列说法正确的个数是( )
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个位似图形若全等,则位似中心在两个图形之间;
④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.
A.1个 B.2个 C.3个 D.4个
17.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点; B.两个图形上的对应线段之比等于相似比
C.两个图形上对应线段必平行 D.两个图形的面积比等于相似比的平方
18.如图27-40所示,在直角坐标系中,A(1,2),B(2,4),C(4,5),D(3,1)围成四边形ABCD.作出四边形ABCD的位似图形,使得新图形与原图形对应线段的比为2∶1,位似中心是坐标原点.
图27-40
19.(1)如图27-41所示,作山四边形ABCD的位似图形A'B'C'D',使四边形ABCD与四边形A'B'C'D'的相似比为2∶1;
(2)若已知AB=2cm,BC=cm,∠A=60°,AB⊥BC,CD⊥DA,
求四边形A'B'C'D'的面积.
图27-41
20.正方形ABCD各顶点的坐标分别为A(1,1),B(-1,1),C(-1,2),D(1,2),以坐标原点为位似中心,将正方形ABCD放大,使放大后的正方形A'B'C'D'的边是正方形边的3倍。(1)写出A'B'C'D'的坐标;(2)直线AC与直线B'D'垂直吗 说明理由.
22.早上小欣与妈妈同时从家里出发,步行与骑自行车到方向相反的两地上学与上班,如图27-46是他们离家的路程y(米)与时间x(分)的函数图象,妈妈骑车走了10分钟时接到小欣的电话,即以原速度骑车前往小欣学校,并与小欣同时到达学校.已知小欣的步行速度为每分50米,求小欣家与学校的距离及小欣早晨上学需要的时间.
图27-46
一、自主学习
1.位似图形上某一对对应顶点到位中心的距离分别为5 cm和15 cm,则它们的相似比为_________
2.如图27-33,蜡烛与成像板之间的距离为3m,小孔纸板距蜡烛1m,若蜡烛AB长20cm,则所成的像长为_________cm.
图27-33
3.四边形ABCD和四边形A'B'C'D'是位似图形,O为位似中心,若OA∶OA',=1∶2,那么AB∶A'B'=________,S四边形ABCD∶S四边形A'B'C'D'=________.
二、基础巩固
4.如图27-34所示,点O是等边△PQR的中心,P,Q',R'分别是OP、OQ、OR的中点,则△P'Q'R'与△PQR是________,点O是_____,相似比是________.
图27-34 图27-35
5.如图27-35所示,矩形AOBC与DOEF是位似图形,且O为位似中心,相似比为1∶,若A(0,1)、B(2,0),则F点的坐标为________.
6.下列两个图形不是位似图形的是( )
7.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A'B'C',的坐标A',(0,3)、B'(6,0)、C(9,6),那么△ABC与△A'B'C'是______图形,位似中心是_______,相似比为________
8.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以-3,得△A'B'C',的坐标A'(0,-3)、B(-6,0)、C'(-9,-6),那么△ABC与△A'B'C'是_____图形,位似中心是_____,相似比为_____.
9.如图27-36所示,按如下方法将△ABC的三边缩小为原来的,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,则下列说法:
(1)△ABC与△DEF是位似形.
(2)△ABC∽△DEF.
(3)△ABC与△DEF周长的比为2∶1
(4)△ABC与△DEF面积的比为4∶1.其中正确的个数是( )
图27-36
A.1 B.2 C.3 D.4
10.图27-36中,△ABC与△DEF是位似图形.那么,DE与AB平行吗 为什么 EF与BC呢 DF与AC呢
三、能力提高
14.有一个正六边形,将其按比例缩小,使得缩小后的正六边形的面积为原正六边形面积的,已知原正六边形一边为3,则后来正六边形的边长为( )
A.9 B.3 C. D.
15.在任意一个三角形内部,画一个小三角形,使其各边与原三角形各边平行,则它们的位似中心是( )
A.一定点 B.原三角形三边垂直平分线的交点
C.原三角形角平分线的交点 D.位置不定的一点
16.下列说法正确的个数是( )
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个位似图形若全等,则位似中心在两个图形之间;
④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.
A.1个 B.2个 C.3个 D.4个
17.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点; B.两个图形上的对应线段之比等于相似比
C.两个图形上对应线段必平行 D.两个图形的面积比等于相似比的平方
18.如图27-40所示,在直角坐标系中,A(1,2),B(2,4),C(4,5),D(3,1)围成四边形ABCD.作出四边形ABCD的位似图形,使得新图形与原图形对应线段的比为2∶1,位似中心是坐标原点.
图27-40
19.(1)如图27-41所示,作山四边形ABCD的位似图形A'B'C'D',使四边形ABCD与四边形A'B'C'D'的相似比为2∶1;
(2)若已知AB=2cm,BC=cm,∠A=60°,AB⊥BC,CD⊥DA,
求四边形A'B'C'D'的面积.
图27-41
20.正方形ABCD各顶点的坐标分别为A(1,1),B(-1,1),C(-1,2),D(1,2),以坐标原点为位似中心,将正方形ABCD放大,使放大后的正方形A'B'C'D'的边是正方形边的3倍。(1)写出A'B'C'D'的坐标;(2)直线AC与直线B'D'垂直吗 说明理由.
22.早上小欣与妈妈同时从家里出发,步行与骑自行车到方向相反的两地上学与上班,如图27-46是他们离家的路程y(米)与时间x(分)的函数图象,妈妈骑车走了10分钟时接到小欣的电话,即以原速度骑车前往小欣学校,并与小欣同时到达学校.已知小欣的步行速度为每分50米,求小欣家与学校的距离及小欣早晨上学需要的时间.
图27-46
