山东省济南一中2013-2014学年高二上学期期末考试数学(文)试题
文档属性
| 名称 | 山东省济南一中2013-2014学年高二上学期期末考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-28 18:36:25 | ||
图片预览


文档简介
济南一中2013-2014学年高二上学期期末考试
数学文试题
说明:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷为第1页至第3页,共20题,第Ⅱ卷为第4页,共8个题。请将第Ⅱ卷答案答在答题纸相应位置,考试结束后将答题纸上交。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,每题5分,共100分)
1.已知全集,,,则等于 ( )
A. B. C. D.
2.函数的定义域是:( )
A. B. C. D.
3. 下列条件中,能判断两个平面平行的是 ( )
A. 一个平面内的一条直线平行于另一个平面;
B. 一个平面内的两条直线平行于另一个平面
C. 一个平面内有无数条直线平行于另一个平面
D. 一个平面内任何一条直线都平行于另一个平面
4. 若直线的倾斜角为,则= ( )
A. 0° B.90° C.45° D.不存在
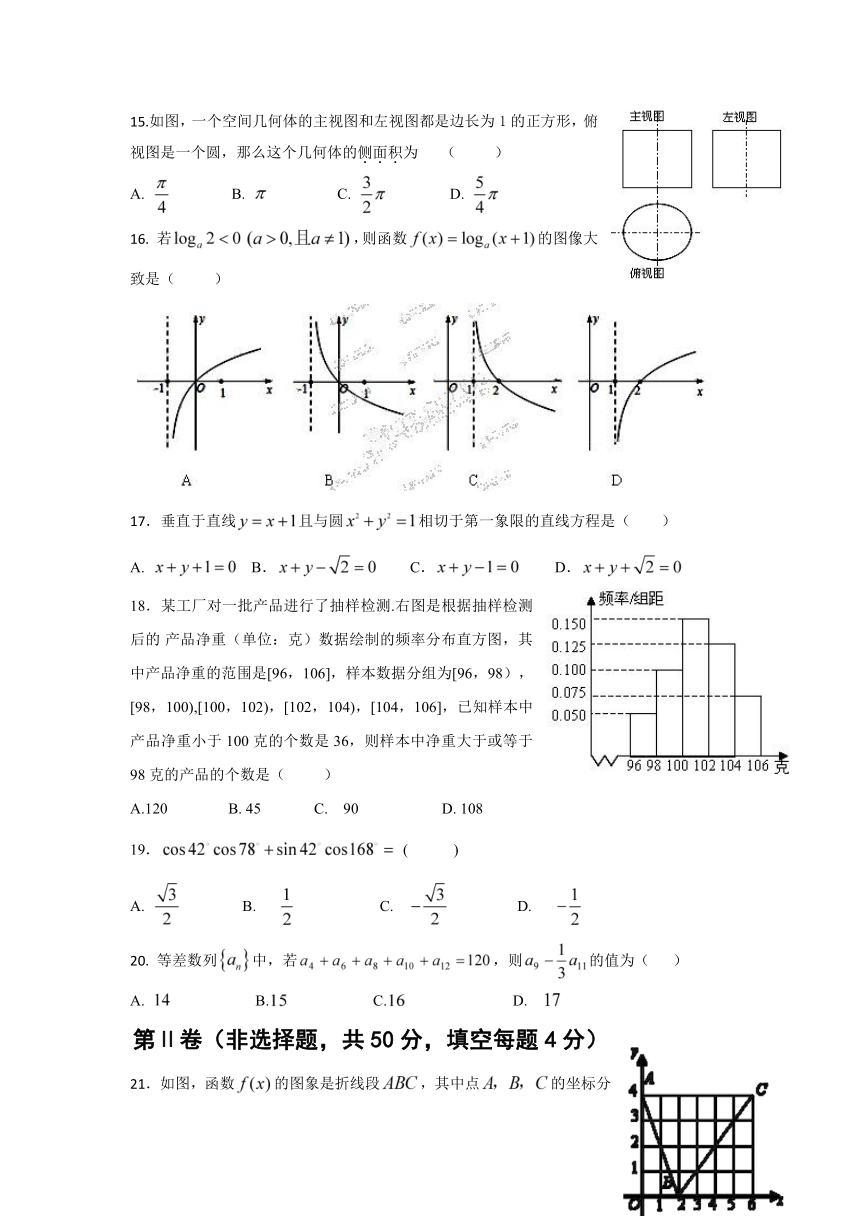
5. 如图所示的程序框图中,当x=1时,输出的y的值是
A. 2 B. 1 C.-2 D.
6.从甲、乙两班分别任意抽出10名学生进行英语口语测验,其测验成绩的方差分别为 ,,则( )
A. 甲班10名学生的成绩比乙班10名学生的成绩整齐
B.乙班10名学生的成绩比甲班10名学生的成绩整齐
C.甲、乙两班10名学生的成绩一样整齐
D.不能比较甲、乙两班10名学生成绩的整齐程度
7.下列向量中,与垂直的向量是( ).
A. B. C. D.
8.已知向量且 // ,则=( )
A. B. C. D.
9.已知中,,,则角等于( )
A. B. C. D.
10.已知成等差数列,成等比数列,则 ( )
A. B.2 C. D.
11.如果满足且,那么下列选项中不一定成立的是( )
A. B. C. D.
12. 命题p:如果,则或.下列叙述正确的个数是( )
① 命题p的逆命题是:如果或,则;
② 命题p的否命题是:如果,则且;
③ 命题p的逆否命题是:如果且,则.
A. 0 B.1 C.2 D.3
13.命题,是的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
14. 已知为第四象限的角,且 ( )
A. B. C. D.
15.如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为 ( )
A. B. C. D.
16. 若,则函数的图像大致是( )
17.垂直于直线且与圆相切于第一象限的直线方程是( )
A. B. C. D.
18.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克的产品的个数是( )
A.120 B. 45 C. 90 D. 108
19. ( )
A. B. C. D.
20. 等差数列中,若,则的值为( )
A. B. C. D.
第Ⅱ卷(非选择题,共50分,填空每题4分)
21.如图,函数的图象是折线段,其中点的坐标分别为,则
22. 函数的最小正周期为_____
23.已知实数条件,则的最大值是______
24. 在中,已知,则角大小为
25. 设是两条不同的直线,是两个不同的平面,给出下列四个命题,
① 若⊥,,则;
② 若;
③ 若; ④ 若.
其中正确命题的序号是 (把所有正确命题的序号都写上)
26.(本题满分8分)已知函数.
(I)求的最小正周期; (II) 求的单调递增区间;
27. (本题满分10分)命题关于的不等式,对一切恒成立,:函数是增函数。若或为真,且为假,求实数的取值范围
28.(本题满分12分)
已知等比数列{}的首项为l,公比q≠1,为其前n项和,分别为某等差数列的第一、第二、第四项.
(I)求和; (Ⅱ)设,数列{}的前n项和为Tn,求证:.
高二文科数学参考答案
27. 命题关于的不等式,对一切恒成立,:函数是增函数。若或为真,且为假,求实数的取值范围
【解】p为真:△=4-16<0 -2<<2, q为真:3-2>1 <1 ...............2分
因为p或q为真,p且q为假 p,q一真一假 ...............4分
当p真q假时, 1≤ ...............6分
当p假q真时, ...............8分
的取值范围为 ...............10分
28.(本小题满分12分)
已知等比数列{}的首项为l,公比q≠1,为其前n项和,分别为某等差数列的第一、第二、第四项.
(I)求和;(Ⅱ)设,数列{}的前n项和为Tn,求证:.
解:(1) 为某等差数列的第一、第二、第四项
................12分
数学文试题
说明:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷为第1页至第3页,共20题,第Ⅱ卷为第4页,共8个题。请将第Ⅱ卷答案答在答题纸相应位置,考试结束后将答题纸上交。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,每题5分,共100分)
1.已知全集,,,则等于 ( )
A. B. C. D.
2.函数的定义域是:( )
A. B. C. D.
3. 下列条件中,能判断两个平面平行的是 ( )
A. 一个平面内的一条直线平行于另一个平面;
B. 一个平面内的两条直线平行于另一个平面
C. 一个平面内有无数条直线平行于另一个平面
D. 一个平面内任何一条直线都平行于另一个平面
4. 若直线的倾斜角为,则= ( )
A. 0° B.90° C.45° D.不存在
5. 如图所示的程序框图中,当x=1时,输出的y的值是
A. 2 B. 1 C.-2 D.
6.从甲、乙两班分别任意抽出10名学生进行英语口语测验,其测验成绩的方差分别为 ,,则( )
A. 甲班10名学生的成绩比乙班10名学生的成绩整齐
B.乙班10名学生的成绩比甲班10名学生的成绩整齐
C.甲、乙两班10名学生的成绩一样整齐
D.不能比较甲、乙两班10名学生成绩的整齐程度
7.下列向量中,与垂直的向量是( ).
A. B. C. D.
8.已知向量且 // ,则=( )
A. B. C. D.
9.已知中,,,则角等于( )
A. B. C. D.
10.已知成等差数列,成等比数列,则 ( )
A. B.2 C. D.
11.如果满足且,那么下列选项中不一定成立的是( )
A. B. C. D.
12. 命题p:如果,则或.下列叙述正确的个数是( )
① 命题p的逆命题是:如果或,则;
② 命题p的否命题是:如果,则且;
③ 命题p的逆否命题是:如果且,则.
A. 0 B.1 C.2 D.3
13.命题,是的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
14. 已知为第四象限的角,且 ( )
A. B. C. D.
15.如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为 ( )
A. B. C. D.
16. 若,则函数的图像大致是( )
17.垂直于直线且与圆相切于第一象限的直线方程是( )
A. B. C. D.
18.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克的产品的个数是( )
A.120 B. 45 C. 90 D. 108
19. ( )
A. B. C. D.
20. 等差数列中,若,则的值为( )
A. B. C. D.
第Ⅱ卷(非选择题,共50分,填空每题4分)
21.如图,函数的图象是折线段,其中点的坐标分别为,则
22. 函数的最小正周期为_____
23.已知实数条件,则的最大值是______
24. 在中,已知,则角大小为
25. 设是两条不同的直线,是两个不同的平面,给出下列四个命题,
① 若⊥,,则;
② 若;
③ 若; ④ 若.
其中正确命题的序号是 (把所有正确命题的序号都写上)
26.(本题满分8分)已知函数.
(I)求的最小正周期; (II) 求的单调递增区间;
27. (本题满分10分)命题关于的不等式,对一切恒成立,:函数是增函数。若或为真,且为假,求实数的取值范围
28.(本题满分12分)
已知等比数列{}的首项为l,公比q≠1,为其前n项和,分别为某等差数列的第一、第二、第四项.
(I)求和; (Ⅱ)设,数列{}的前n项和为Tn,求证:.
高二文科数学参考答案
27. 命题关于的不等式,对一切恒成立,:函数是增函数。若或为真,且为假,求实数的取值范围
【解】p为真:△=4-16<0 -2<<2, q为真:3-2>1 <1 ...............2分
因为p或q为真,p且q为假 p,q一真一假 ...............4分
当p真q假时, 1≤ ...............6分
当p假q真时, ...............8分
的取值范围为 ...............10分
28.(本小题满分12分)
已知等比数列{}的首项为l,公比q≠1,为其前n项和,分别为某等差数列的第一、第二、第四项.
(I)求和;(Ⅱ)设,数列{}的前n项和为Tn,求证:.
解:(1) 为某等差数列的第一、第二、第四项
................12分
同课章节目录
