数学人教A版(2019)必修第二册7.1复数的概念 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册7.1复数的概念 课件(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-19 06:16:54 | ||
图片预览






文档简介
(共18张PPT)
必修第二册第七章《复数》
7.1 复数的概念
必修第二册第七章《复数》
7.1.1 数系的扩充和复数的概念
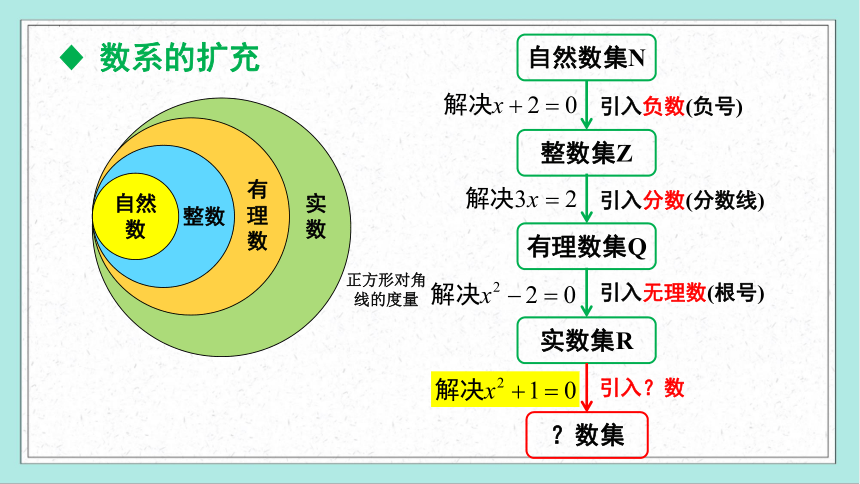
数系的扩充
自然数集N
整数集Z
引入负数(负号)
引入分数(分数线)
有理数集Q
引入无理数(根号)
实数集R
自然数
整数
有
理
数
实
数
引入?数
?数集
正方形对角线的度量
复数是16世纪人们在讨论一元二次方程、一元三次方程的求根公式时引入的。
复数在数学、力学、电学及其他学科中都有广泛的应用。
复数与向量、平面解析几何、三角函数等都有密切的联系。
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
如:Q中的加/乘法交换律、结合律等
R中也适用
引入虚数i,使i2=﹣1
解决问题,引入新数
实数
i
解决方程x2+1=0在实数集中无解的问题:
②引入i后的新数集和实数间仍能进行加/乘法运算.
①引入新数i,使i 2 = i·i = -1;
③扩充为新数集C={a+bi|a,b∈R}.
a+bi
复数集
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
1.复数集和复数的概念-P69
实数
虚数
纯虚数
复数C
R
[例1]实数x取什么值时,
复数z=(x2+2x-3)+(x+3)i是:
(1)实数? (2)虚数? (3)纯虚数?
x=﹣3
x≠﹣3
x=1
2.虚数单位 i
B
虚数单位“i”是数学家欧拉最早引入的,到德国数学家高斯提倡才普遍使用。
高斯第一个引进术语“复数”并记作a+bi。“虚数”一词首先由笛卡儿提出。
-1-i
3.复数相等-P69
一般对两个不全是实数的复数只能说相等或不相等,不能比较大小.
如:3与1+2i不能比较大小
2+3i与1+2i不能比较大小.
作用:将复数问题转化为实数问题.
注:若两个复数能比较大小,则它们必为实数.
3.复数相等-P69
复系数一元二次方程是否有根不能用△判定.
复系数一元二次方程
是否有根不能用△判定.
必修第二册第七章《复数》
7.1.2 复数的几何意义
历史上,复数一开始也叫做虚数,因为数学家们感觉它很“虚幻”,难以认识.
复数是否像实数一样可在现实世界中找到她的“影子”呢?
实数a
数轴上的点a
一一对应
复平面
任一复数z=a+bi都可由一个有序实数对(a,b)唯一确定.
复数z=a+bi
平面直角坐标系内的点(a,b)
一一对应
复数z=a+bi
复平面内的点Z(a,b)
一一对应
4.复数的几何意义 P70-71
平面向量OZ=(a,b)
一一对应
→
①建立了直角坐标系来表示复数的平面叫复平面;
x轴叫实轴,y轴叫虚轴.
②实轴上的点都表示实数(b=0);
③虚轴上的点(除原点外)都表示纯虚数(a=0,b≠0);
<0
>0
二
5.复数的模 P71
规定:相等的向量表示同一个复数.
考查1:|z|的计算公式
5.复数的模 P71
考查2:|z|的几何意义
6.共轭复数
实部相等,虚部互为相反数的两个复数叫做共轭复数.
本意:两头牛背上的架子称为轭,轭使两头牛同步行走。共轭即为按一定的规律相配的一对。
必修第二册第七章《复数》
7.1 复数的概念
必修第二册第七章《复数》
7.1.1 数系的扩充和复数的概念
数系的扩充
自然数集N
整数集Z
引入负数(负号)
引入分数(分数线)
有理数集Q
引入无理数(根号)
实数集R
自然数
整数
有
理
数
实
数
引入?数
?数集
正方形对角线的度量
复数是16世纪人们在讨论一元二次方程、一元三次方程的求根公式时引入的。
复数在数学、力学、电学及其他学科中都有广泛的应用。
复数与向量、平面解析几何、三角函数等都有密切的联系。
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
如:Q中的加/乘法交换律、结合律等
R中也适用
引入虚数i,使i2=﹣1
解决问题,引入新数
实数
i
解决方程x2+1=0在实数集中无解的问题:
②引入i后的新数集和实数间仍能进行加/乘法运算.
①引入新数i,使i 2 = i·i = -1;
③扩充为新数集C={a+bi|a,b∈R}.
a+bi
复数集
扩充后的数系中规定的加/乘法运算与原数系的加/乘法运算协调一致.
1.复数集和复数的概念-P69
实数
虚数
纯虚数
复数C
R
[例1]实数x取什么值时,
复数z=(x2+2x-3)+(x+3)i是:
(1)实数? (2)虚数? (3)纯虚数?
x=﹣3
x≠﹣3
x=1
2.虚数单位 i
B
虚数单位“i”是数学家欧拉最早引入的,到德国数学家高斯提倡才普遍使用。
高斯第一个引进术语“复数”并记作a+bi。“虚数”一词首先由笛卡儿提出。
-1-i
3.复数相等-P69
一般对两个不全是实数的复数只能说相等或不相等,不能比较大小.
如:3与1+2i不能比较大小
2+3i与1+2i不能比较大小.
作用:将复数问题转化为实数问题.
注:若两个复数能比较大小,则它们必为实数.
3.复数相等-P69
复系数一元二次方程是否有根不能用△判定.
复系数一元二次方程
是否有根不能用△判定.
必修第二册第七章《复数》
7.1.2 复数的几何意义
历史上,复数一开始也叫做虚数,因为数学家们感觉它很“虚幻”,难以认识.
复数是否像实数一样可在现实世界中找到她的“影子”呢?
实数a
数轴上的点a
一一对应
复平面
任一复数z=a+bi都可由一个有序实数对(a,b)唯一确定.
复数z=a+bi
平面直角坐标系内的点(a,b)
一一对应
复数z=a+bi
复平面内的点Z(a,b)
一一对应
4.复数的几何意义 P70-71
平面向量OZ=(a,b)
一一对应
→
①建立了直角坐标系来表示复数的平面叫复平面;
x轴叫实轴,y轴叫虚轴.
②实轴上的点都表示实数(b=0);
③虚轴上的点(除原点外)都表示纯虚数(a=0,b≠0);
<0
>0
二
5.复数的模 P71
规定:相等的向量表示同一个复数.
考查1:|z|的计算公式
5.复数的模 P71
考查2:|z|的几何意义
6.共轭复数
实部相等,虚部互为相反数的两个复数叫做共轭复数.
本意:两头牛背上的架子称为轭,轭使两头牛同步行走。共轭即为按一定的规律相配的一对。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
