3.9 弧长及扇形的面积 课件(共24张PPT)
文档属性
| 名称 | 3.9 弧长及扇形的面积 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 09:21:54 | ||
图片预览






文档简介
(共24张PPT)
3.9 弧长及扇形的面积
北师大版 九年级 下册
教学目标
教学目标: 1.理解弧长和扇形面积公式的推导过程.
2.灵活运用弧长及扇形面积公式解决实际问题.
教学重点: 理解弧长和扇形面积公式的推导过程.
教学难点:利用弧长和扇形面积公式进行计算.
新知讲解
情境引入
问题1 你注意到了吗,在运动会的4×100米比赛中,各选手的起跑线不再同一处,你知道这是为什么吗?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
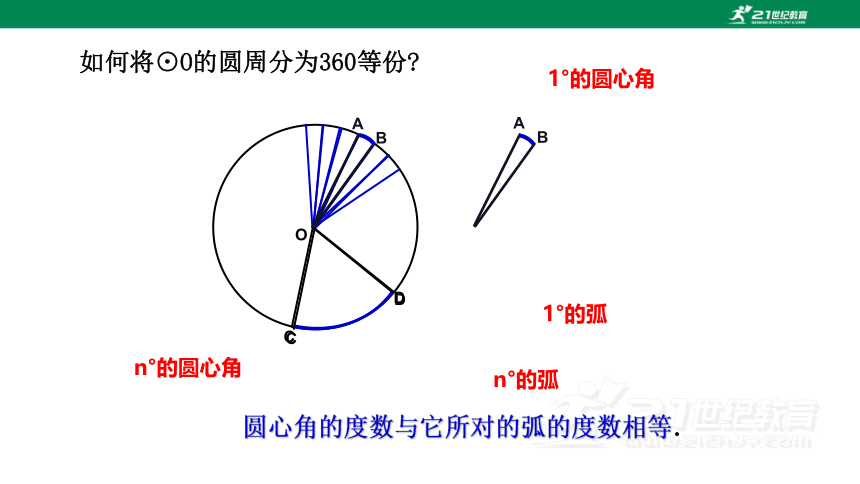
O
●
C
D
A
B
A
B
1°的圆心角
1°的弧
C
D
n°的圆心角
n°的弧
圆心角的度数与它所对的弧的度数相等.
如何将⊙O的圆周分为360等份
探索与思考(半径R) 圆心角 所对的圆弧
360°
1°
90°
n°
合作学习
如图,某传送带的一个转动轮的
半径为10cm.
(2)转动轮转1°,传送带上的物
品A被传送多少厘米?
(1)转动轮转1周,传送带上的物
品A被传送多少厘米?
(3)转动轮转n°,传送带上的物
品A被传送多少厘米?
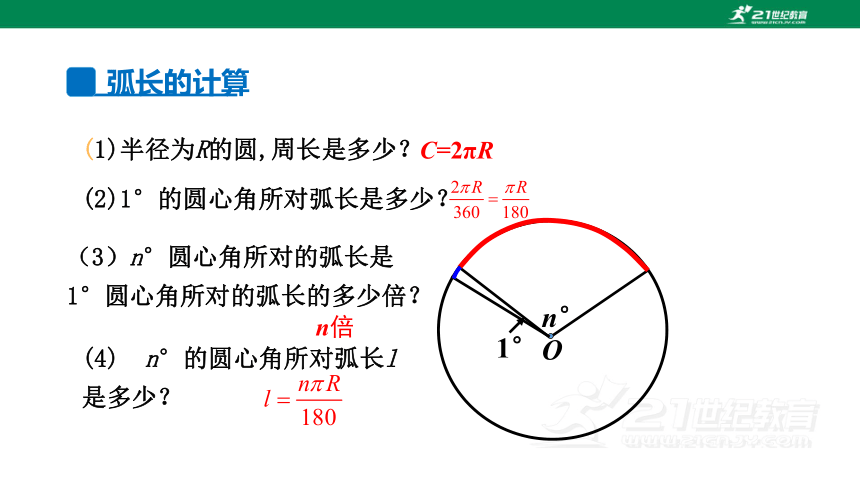
(1)半径为R的圆,周长是多少?
(2)1°的圆心角所对弧长是多少?
n°
O
(4) n°的圆心角所对弧长l是多少?
1°
C=2πR
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
弧长的计算
提炼概念
在半径为R的圆中,n°的圆心角所对弧长的计算公式为:
(1)用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
典例精讲
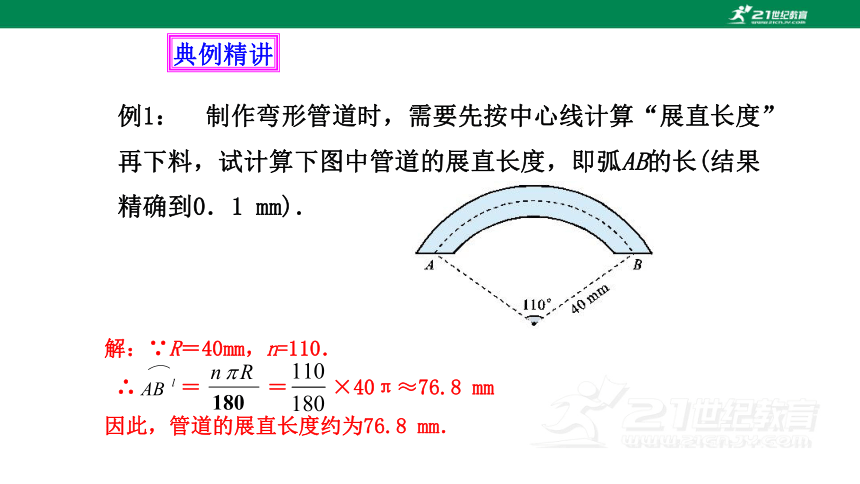
例1: 制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即弧AB的长(结果精确到0.1 mm).
解:∵R=40mm,n=110.
∴ = = ×40π≈76.8 mm
因此,管道的展直长度约为76.8 mm.
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端栓着一只狗.
(1)这只狗的最大活动区域有多大?
n°
(2)如果这只狗只能绕柱子转过 n°角,那么它的最大活动区域有多大?
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
n°
R
R
l
扇形的周长是_______.
扇形的面积是____________.
在(2)问里狗活动的区域是一个什么图形呢?
2R+l
S=πR2
(2)圆心角为1°的扇形的面积是多少
(3)圆心角为n°的扇形的面积是圆心角为1°
的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少
思考
(1)半径为R的圆,面积是多少?
合作探究
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
类比学习
例2 如图,已知圆O的半径12cm,圆心角∠AOB=120o,求AB的长(结果精确到0.1cm2)和扇形OAB的面积(结果精确到0.1cm2).
(
解:AB=
(
为什么这二种解法会产生答案不同,主要是弧长计算时已经是约数了,如果要用第二种解法,弧长要么写成分数,要么多精确一位.
归纳概念
(1)当已知弧长 l 和半径 R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
课堂练习
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π B.2π C.3π D.6π
2.已知一个扇形的半径为6,弧长为2π,则这个扇形的圆心角为( )
A.30° B.60° C.90° D.120°
C
B
3.如图,AC是☉O的直径,B,D是☉O上的点,若☉O的半径为3,∠ADB=30°,则的长为 .
2π
180°
4.若一个扇形的半径为2 cm,面积为2π cm2,则此扇形的圆心角为 .
解析:连接OB、OC,
∵AB是⊙O的切线,∴AB⊥BO.
∵∠A=30°,∴∠AOB=60°.
∵BC∥AO,∴∠OBC=∠AOB=60°.
在等腰△OBC中,
∠BOC=180°-2∠OBC=180°-2×60°=60°.
∴BC的长为 =2π(cm).
故答案为2π.
5.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO.若∠A=30°,则劣弧BC的长为多少cm?
︵
︵
6.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
课堂总结
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.9 弧长及扇形的面积
北师大版 九年级 下册
教学目标
教学目标: 1.理解弧长和扇形面积公式的推导过程.
2.灵活运用弧长及扇形面积公式解决实际问题.
教学重点: 理解弧长和扇形面积公式的推导过程.
教学难点:利用弧长和扇形面积公式进行计算.
新知讲解
情境引入
问题1 你注意到了吗,在运动会的4×100米比赛中,各选手的起跑线不再同一处,你知道这是为什么吗?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
O
●
C
D
A
B
A
B
1°的圆心角
1°的弧
C
D
n°的圆心角
n°的弧
圆心角的度数与它所对的弧的度数相等.
如何将⊙O的圆周分为360等份
探索与思考(半径R) 圆心角 所对的圆弧
360°
1°
90°
n°
合作学习
如图,某传送带的一个转动轮的
半径为10cm.
(2)转动轮转1°,传送带上的物
品A被传送多少厘米?
(1)转动轮转1周,传送带上的物
品A被传送多少厘米?
(3)转动轮转n°,传送带上的物
品A被传送多少厘米?
(1)半径为R的圆,周长是多少?
(2)1°的圆心角所对弧长是多少?
n°
O
(4) n°的圆心角所对弧长l是多少?
1°
C=2πR
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
弧长的计算
提炼概念
在半径为R的圆中,n°的圆心角所对弧长的计算公式为:
(1)用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,而只有在同圆或等圆中,才可能是等弧.
典例精讲
例1: 制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即弧AB的长(结果精确到0.1 mm).
解:∵R=40mm,n=110.
∴ = = ×40π≈76.8 mm
因此,管道的展直长度约为76.8 mm.
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端栓着一只狗.
(1)这只狗的最大活动区域有多大?
n°
(2)如果这只狗只能绕柱子转过 n°角,那么它的最大活动区域有多大?
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
n°
R
R
l
扇形的周长是_______.
扇形的面积是____________.
在(2)问里狗活动的区域是一个什么图形呢?
2R+l
S=πR2
(2)圆心角为1°的扇形的面积是多少
(3)圆心角为n°的扇形的面积是圆心角为1°
的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少
思考
(1)半径为R的圆,面积是多少?
合作探究
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
类比学习
例2 如图,已知圆O的半径12cm,圆心角∠AOB=120o,求AB的长(结果精确到0.1cm2)和扇形OAB的面积(结果精确到0.1cm2).
(
解:AB=
(
为什么这二种解法会产生答案不同,主要是弧长计算时已经是约数了,如果要用第二种解法,弧长要么写成分数,要么多精确一位.
归纳概念
(1)当已知弧长 l 和半径 R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
课堂练习
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π B.2π C.3π D.6π
2.已知一个扇形的半径为6,弧长为2π,则这个扇形的圆心角为( )
A.30° B.60° C.90° D.120°
C
B
3.如图,AC是☉O的直径,B,D是☉O上的点,若☉O的半径为3,∠ADB=30°,则的长为 .
2π
180°
4.若一个扇形的半径为2 cm,面积为2π cm2,则此扇形的圆心角为 .
解析:连接OB、OC,
∵AB是⊙O的切线,∴AB⊥BO.
∵∠A=30°,∴∠AOB=60°.
∵BC∥AO,∴∠OBC=∠AOB=60°.
在等腰△OBC中,
∠BOC=180°-2∠OBC=180°-2×60°=60°.
∴BC的长为 =2π(cm).
故答案为2π.
5.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO.若∠A=30°,则劣弧BC的长为多少cm?
︵
︵
6.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
课堂总结
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
