八年级下册数学期末测试题(一)(含解析)
文档属性
| 名称 | 八年级下册数学期末测试题(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 09:33:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级下册数学期末测试题(一)
(时间:90分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.“柳条初弄绿,已觉春风驻.”每到春天,人们在欣赏桃红柳绿的同时,也被飞舞的柳絮所烦恼.据了解柳絮纤维的直径约为0.00105 cm,则0.00105用科学记数法可表示为( )
2.下列运算正确的是( )
3.若 则的值为 ( )
4.正方形边长为5厘米,若边长减少x(厘米),则面积减少y (平方厘米).下列说法正确的是 ( )
A.边长x是自变量,面积减少量y是因变量 B.边长是自变量,面积是因变量
C.上述关系式为 y=( 5-x) D.上述关系式为 y=5 -(5-x)
5.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以
④因为A,M,B在同一条直线上,且AM=BM,所以M是AB中点.
其中正确的是 ( )
A.①③④ B.④ C.②③④ D.③④
6.如图,赵老师在点O处观测到小明站位点A位于北偏西 的方向,同时观测到小刚站位点B在南偏的方向,那么∠AOB的大小是( )
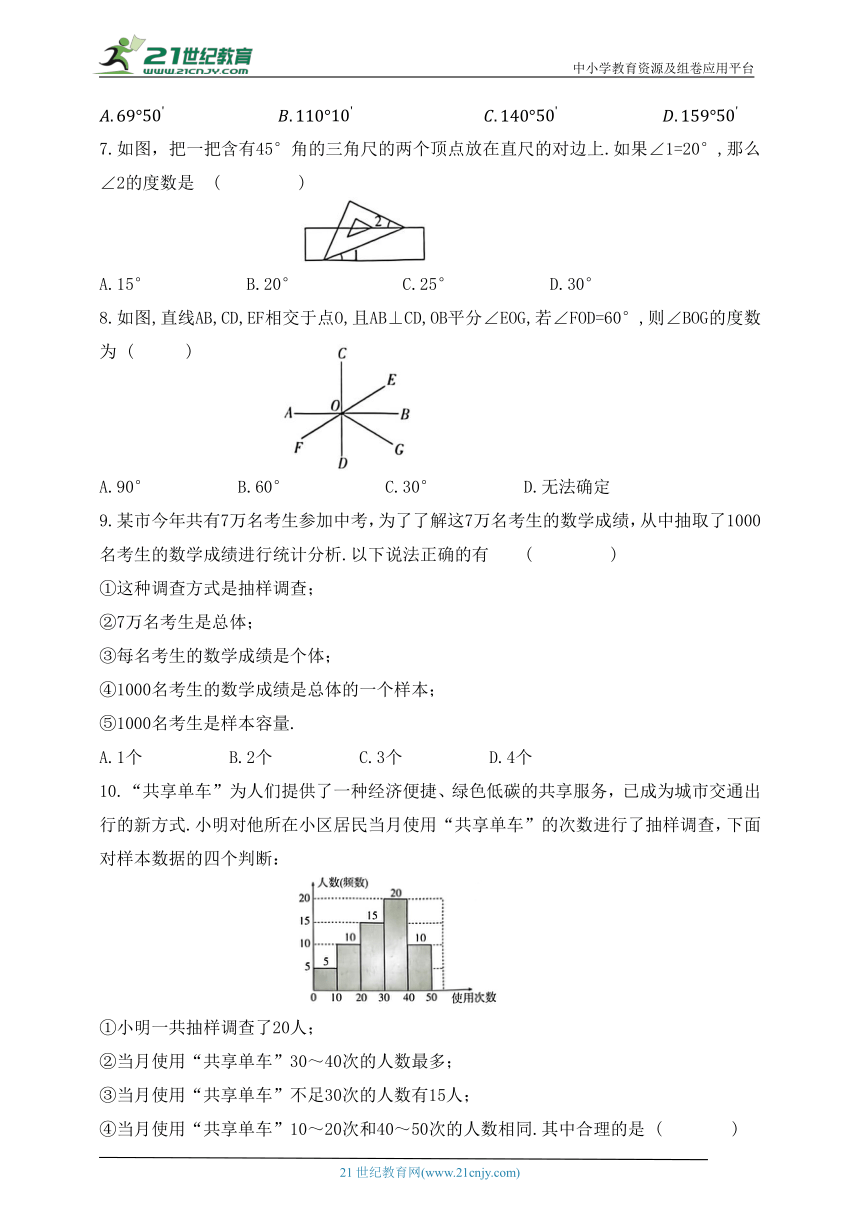
7.如图,把一把含有45°角的三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 ( )
A.15° B.20° C.25° D.30°
8.如图,直线AB,CD,EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°,则∠BOG的度数为 ( )
A.90° B.60° C.30° D.无法确定
9.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有 ( )
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1个 B.2个 C.3个 D.4个
10.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,已成为城市交通出行的新方式.小明对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,下面对样本数据的四个判断:
①小明一共抽样调查了20人;
②当月使用“共享单车”30~40次的人数最多;
③当月使用“共享单车”不足30次的人数有15人;
④当月使用“共享单车”10~20次和40~50次的人数相同.其中合理的是 ( )
A.①② B.②③ C.②④ D.③④
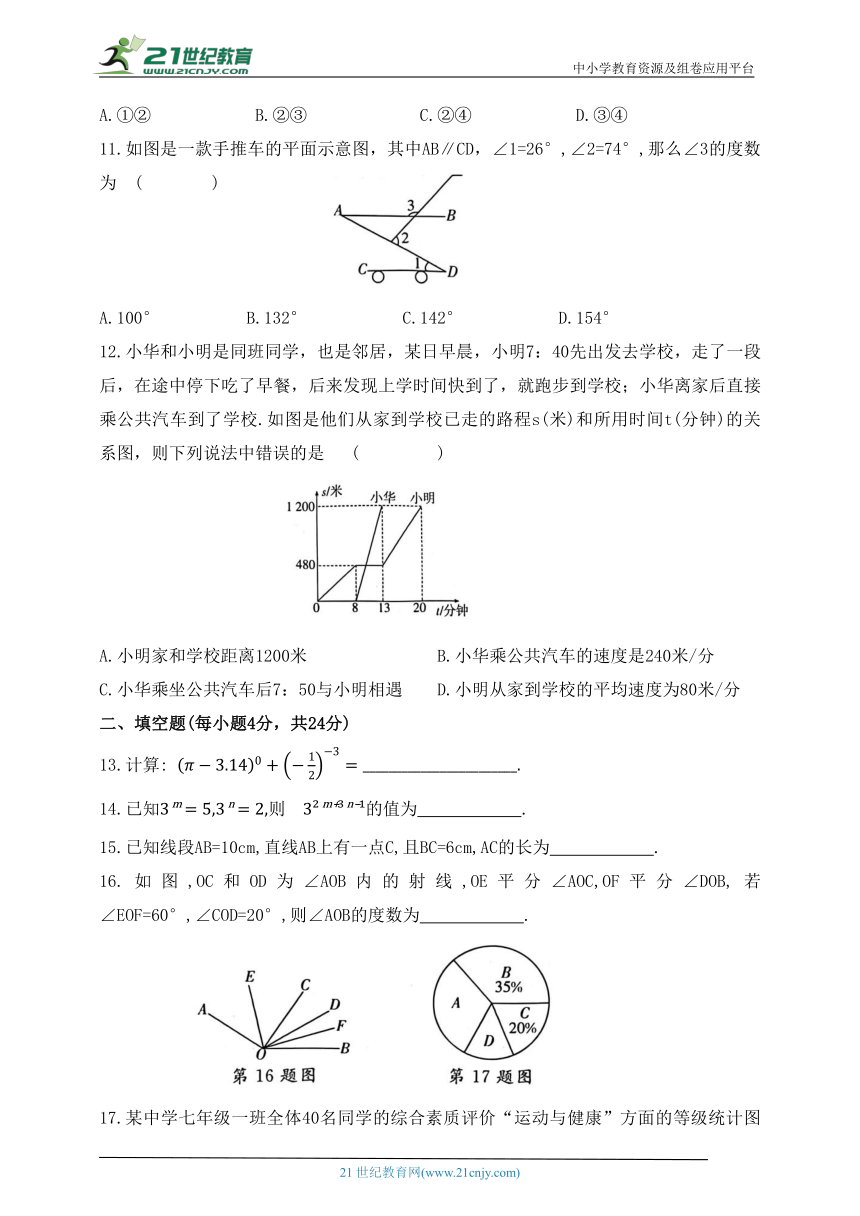
11.如图是一款手推车的平面示意图,其中AB∥CD,∠1=26°,∠2=74°,那么∠3的度数为 ( )
A.100° B.132° C.142° D.154°
12.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图,则下列说法中错误的是 ( )
A.小明家和学校距离1200米 B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇 D.小明从家到学校的平均速度为80米/分
二、填空题(每小题4分,共24分)
13.计算:
14.已知则 的值为 .
15.已知线段AB=10cm,直线AB上有一点C,且BC=6cm,AC的长为 .
16.如图,OC和OD为∠AOB内的射线,OE平分∠AOC,OF平分∠DOB,若∠EOF=60°,∠COD=20°,则∠AOB的度数为 .
17.某中学七年级一班全体40名同学的综合素质评价“运动与健康”方面的等级统计图如图所示,其中评价为“A”等级的百分比是“D”等级的2倍,则评价为“A”等级有 人.
18.如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市C地,它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有 km.
三、解答题(共78分)
19.(8分)
(1)计算:;
(2)已知关于x的多项式的展开式中不含x 项,而三次项为.
化简求值:.
20.(8分)若x+y=6,且(x+2)(y+2)=24.
(1)求xy的值;
(2)求x +y 的值;
(3)求x +y 的值.
21.(10分)在数轴上,点A表示2.4,点B表示-3.6,点C表示-0.6.
(1)求线段AB的长.
(2)点C是不是线段AB的中点,为什么
(3)取线段BC的中点D,那么点D表示什么数
22.(10分)如图,AD∥EF,∠1+∠2=180°.
(1)若∠1=50°,求∠BAD的度数.
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.
23.(14分)如图,O是直线AB上的一点,∠COD是直角,OE 平分∠BOC.
(1)若∠AOC=30°时,则∠DOE= .
(2)将图1中的∠COD绕顶点O顺时针旋转至图2的位置,其他条件不变,探究∠AOC和∠DOE之间的数量关系,写出你的结论,并说明理由.
(3)将图1中的∠COD绕顶点O顺时针旋转至图3的位置,其他条件不变,探究∠AOC和∠DOE之间的数量关系,写出你的结论,并说明理由.
24.(14分)中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了某区若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成:D.反对).并将调查结果绘制成折线统计图和扇形统计图(不完整).请根据图中提供的信息,解答下列问题.
(1)此次抽样调查中,共调查了 名中学生家长.
(2)扇形统计图中,表示A类型的扇形圆心角的度数为 .
(3)先求出C类型的人数,然后将图1中的折线统计图补充完整.
(4)根据抽样调查结果,请你估计该区18000名中学生家长中有多少名家长持反对态度
25.(14分)“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系.
请你根据图中给出的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系;赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米 乌龟每分钟爬多少米
(3)乌龟从出发到追上兔子用了多少分钟
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟
参考答案
1. B 2. A 3. C 4. D 5. C 6. C 7. C 8. C 9. C 10. C
11. B 【解析】如图,作EF∥AB,
∵AB∥CD,∴EF∥AB∥CD.
∵∠1=26°,∴∠DEF=∠1=26°.
∵∠2=74°,∴∠HEF=∠DEH-∠DEF=74°-26°=48°,
∴∠BHE=180°-∠HEF=132°,∴∠3=∠BHE=132°.故选B.
12. D 【解析】由图象可知,小华和小明的家离学校1200米,故A正确;根据图象,小华乘公共汽车,从出发到到达学校共用了13-8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.故选D.
13.-7
14. 【解析】∵∴.
15.4cm或16 cm 【解析】有两种情况:
(1)当点C在线段AB上时,如图①,AC=AB-BC.
又∵AB=10cm,BC=6cm,∴AC=10-6=4(cm);
(2)当点C在线段AB的延长线上时,如图②,AC=AB+BC.又∵AB=10cm,BC=6cm,∴AC=10+6=16(cm).
16.100° 17.12
18.120 【解析】摩托车比汽车晚到4-3=1(h),因为汽车和摩托车分别从A,B两地去同一城市C,从y轴上可看出A,B 两地的路程为20km,故汽车的速度为180÷3=60(km/h);摩托车的速度为(180-20)÷4=40(km/h);设出发xh后两车相遇,根据题意,得20+40x=60x,解得x=1,即出发1h 后两车相遇,180-60=120(km),即两车相遇时距离C地还有120km.故答案为:120.
19.解: (1)[(a+b) +( a-b) ][( 1-a)(a+1)+( b+1)(b-1)]
=(a +2ab+b +a -2ab+b )(1-a +b -1)
=2(a +b )(b -a )=2b -2a .
(2)(x +mx+3)(x +nx+3)=x +(mn+6)x +(3m+3n)x+(m+n)x +9.
∵关于x的多项式 (x +mx+3)(x +nx+3)的展开式中不含x 项,而三次项为5x ,
∴mn+6=0,m+n=5,∴mn=-6,m+n=5,故m=6,n=-1.
∴(m+n+1)(m+n-1)+(2m n-mn -m )÷(-m)
=(m+n) -1+( -2mn+n +m )
=(m+n) -1+[(m+n) -4mn]
=5 -1+[5 -4×( -6)]=73.
20.解: (1)∵(x+2)(y+2)=xy+2x+2y+4=xy+2(x+y)=20.且x+y=6,∴xy=20-2×6=8.
(2)∵x+y=6,xy=8,∴x +y =(x+y) -2xy=6 -2×8=20.
(3)∵x +y =20,xy=8,∴x +y =(x +y ) -2(xy) =20 -2×8 =272.
21.解:如图,
∵点A表示2.4,点B表示-3.6,点C表示-0.6,∴OA=2.4,OB=3.6,OC=0.6.
(1)线段AB=OA+OB=2.4+3.6=6.
(2)点C是线段AB的中点.理由如下:
∵AC=OA+OC=2.4+0.6=3,BC=OB-OC=3.6-0.6=3,∴AC=BC,即C是线段AB的中点.
(3)设D的坐标为x,即BD=CD,则有:(-0.6)-x=x-(-3.6),解得x=-2.1.
∴点D表示的数是-2.1.
22.(1)解:∵AD∥EF,∴∠BAD+∠2=180°.
∵∠1+∠2=180°,∴∠1=∠BAD.
∵∠1=50°,∴∠BAD=50°.
(2)证明:∵DG⊥AC,∴∠DGC=90°.
∵∠BAC=90°,∴∠BAC=∠DGC,∴AB∥DG,∴∠BAD=∠ADG.
由(1)得∠1=∠BAD,∴∠1=∠ADG,∴DG平分∠ADC.
23.解:(1)∵∠AOC=30°,∴∠BOC=180°-∠AOC=150°.
又∵∠COD是直角,OE平分∠BOC,
(2)∠AOC=2∠DOE.理由如下:
∵∠COD是直角,OE平分∠BOC,∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE)=2∠DOE.
(3)∠AOC=360°-2∠DOE.理由如下:
∵OE平分∠BOC,∴∠BOC=2∠COE,
∴∠AOC=180° -∠BOC=180° -2∠COE=180° -2(∠DOE-90°)=360°-2∠DOE.
24.解:(1)本次调查的家长有:30÷15%=200(名),故答案为200.
(2)A类型的扇形圆心角的度数为360°×15%=54°,故答案为54°.
(3)由题意可得,C类型的家长有:200-30-40-120=10(名),补全的折线统计图,如图所示.
(4)由题意,可得 (名),
即该市区18000名中学生家长中有10800名家长持反对态度.
25.解:(1)兔子 乌龟 1500
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50(米),∴乌龟每分钟爬50米.
(3)700÷50=14(分钟),∴乌龟用了14分钟追上了正在睡觉的兔子.
(4)∵48千米=48000米,
∴48000÷60=800(米/分),(1500-700)÷800=1(分钟),30+0.5-1×2=28.5(分钟),
∴兔子中间停下睡觉用了28.5分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
八年级下册数学期末测试题(一)
(时间:90分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.“柳条初弄绿,已觉春风驻.”每到春天,人们在欣赏桃红柳绿的同时,也被飞舞的柳絮所烦恼.据了解柳絮纤维的直径约为0.00105 cm,则0.00105用科学记数法可表示为( )
2.下列运算正确的是( )
3.若 则的值为 ( )
4.正方形边长为5厘米,若边长减少x(厘米),则面积减少y (平方厘米).下列说法正确的是 ( )
A.边长x是自变量,面积减少量y是因变量 B.边长是自变量,面积是因变量
C.上述关系式为 y=( 5-x) D.上述关系式为 y=5 -(5-x)
5.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以
④因为A,M,B在同一条直线上,且AM=BM,所以M是AB中点.
其中正确的是 ( )
A.①③④ B.④ C.②③④ D.③④
6.如图,赵老师在点O处观测到小明站位点A位于北偏西 的方向,同时观测到小刚站位点B在南偏的方向,那么∠AOB的大小是( )
7.如图,把一把含有45°角的三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 ( )
A.15° B.20° C.25° D.30°
8.如图,直线AB,CD,EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°,则∠BOG的度数为 ( )
A.90° B.60° C.30° D.无法确定
9.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有 ( )
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1个 B.2个 C.3个 D.4个
10.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,已成为城市交通出行的新方式.小明对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,下面对样本数据的四个判断:
①小明一共抽样调查了20人;
②当月使用“共享单车”30~40次的人数最多;
③当月使用“共享单车”不足30次的人数有15人;
④当月使用“共享单车”10~20次和40~50次的人数相同.其中合理的是 ( )
A.①② B.②③ C.②④ D.③④
11.如图是一款手推车的平面示意图,其中AB∥CD,∠1=26°,∠2=74°,那么∠3的度数为 ( )
A.100° B.132° C.142° D.154°
12.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图,则下列说法中错误的是 ( )
A.小明家和学校距离1200米 B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇 D.小明从家到学校的平均速度为80米/分
二、填空题(每小题4分,共24分)
13.计算:
14.已知则 的值为 .
15.已知线段AB=10cm,直线AB上有一点C,且BC=6cm,AC的长为 .
16.如图,OC和OD为∠AOB内的射线,OE平分∠AOC,OF平分∠DOB,若∠EOF=60°,∠COD=20°,则∠AOB的度数为 .
17.某中学七年级一班全体40名同学的综合素质评价“运动与健康”方面的等级统计图如图所示,其中评价为“A”等级的百分比是“D”等级的2倍,则评价为“A”等级有 人.
18.如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市C地,它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有 km.
三、解答题(共78分)
19.(8分)
(1)计算:;
(2)已知关于x的多项式的展开式中不含x 项,而三次项为.
化简求值:.
20.(8分)若x+y=6,且(x+2)(y+2)=24.
(1)求xy的值;
(2)求x +y 的值;
(3)求x +y 的值.
21.(10分)在数轴上,点A表示2.4,点B表示-3.6,点C表示-0.6.
(1)求线段AB的长.
(2)点C是不是线段AB的中点,为什么
(3)取线段BC的中点D,那么点D表示什么数
22.(10分)如图,AD∥EF,∠1+∠2=180°.
(1)若∠1=50°,求∠BAD的度数.
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.
23.(14分)如图,O是直线AB上的一点,∠COD是直角,OE 平分∠BOC.
(1)若∠AOC=30°时,则∠DOE= .
(2)将图1中的∠COD绕顶点O顺时针旋转至图2的位置,其他条件不变,探究∠AOC和∠DOE之间的数量关系,写出你的结论,并说明理由.
(3)将图1中的∠COD绕顶点O顺时针旋转至图3的位置,其他条件不变,探究∠AOC和∠DOE之间的数量关系,写出你的结论,并说明理由.
24.(14分)中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了某区若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成:D.反对).并将调查结果绘制成折线统计图和扇形统计图(不完整).请根据图中提供的信息,解答下列问题.
(1)此次抽样调查中,共调查了 名中学生家长.
(2)扇形统计图中,表示A类型的扇形圆心角的度数为 .
(3)先求出C类型的人数,然后将图1中的折线统计图补充完整.
(4)根据抽样调查结果,请你估计该区18000名中学生家长中有多少名家长持反对态度
25.(14分)“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系.
请你根据图中给出的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系;赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米 乌龟每分钟爬多少米
(3)乌龟从出发到追上兔子用了多少分钟
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟
参考答案
1. B 2. A 3. C 4. D 5. C 6. C 7. C 8. C 9. C 10. C
11. B 【解析】如图,作EF∥AB,
∵AB∥CD,∴EF∥AB∥CD.
∵∠1=26°,∴∠DEF=∠1=26°.
∵∠2=74°,∴∠HEF=∠DEH-∠DEF=74°-26°=48°,
∴∠BHE=180°-∠HEF=132°,∴∠3=∠BHE=132°.故选B.
12. D 【解析】由图象可知,小华和小明的家离学校1200米,故A正确;根据图象,小华乘公共汽车,从出发到到达学校共用了13-8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.故选D.
13.-7
14. 【解析】∵∴.
15.4cm或16 cm 【解析】有两种情况:
(1)当点C在线段AB上时,如图①,AC=AB-BC.
又∵AB=10cm,BC=6cm,∴AC=10-6=4(cm);
(2)当点C在线段AB的延长线上时,如图②,AC=AB+BC.又∵AB=10cm,BC=6cm,∴AC=10+6=16(cm).
16.100° 17.12
18.120 【解析】摩托车比汽车晚到4-3=1(h),因为汽车和摩托车分别从A,B两地去同一城市C,从y轴上可看出A,B 两地的路程为20km,故汽车的速度为180÷3=60(km/h);摩托车的速度为(180-20)÷4=40(km/h);设出发xh后两车相遇,根据题意,得20+40x=60x,解得x=1,即出发1h 后两车相遇,180-60=120(km),即两车相遇时距离C地还有120km.故答案为:120.
19.解: (1)[(a+b) +( a-b) ][( 1-a)(a+1)+( b+1)(b-1)]
=(a +2ab+b +a -2ab+b )(1-a +b -1)
=2(a +b )(b -a )=2b -2a .
(2)(x +mx+3)(x +nx+3)=x +(mn+6)x +(3m+3n)x+(m+n)x +9.
∵关于x的多项式 (x +mx+3)(x +nx+3)的展开式中不含x 项,而三次项为5x ,
∴mn+6=0,m+n=5,∴mn=-6,m+n=5,故m=6,n=-1.
∴(m+n+1)(m+n-1)+(2m n-mn -m )÷(-m)
=(m+n) -1+( -2mn+n +m )
=(m+n) -1+[(m+n) -4mn]
=5 -1+[5 -4×( -6)]=73.
20.解: (1)∵(x+2)(y+2)=xy+2x+2y+4=xy+2(x+y)=20.且x+y=6,∴xy=20-2×6=8.
(2)∵x+y=6,xy=8,∴x +y =(x+y) -2xy=6 -2×8=20.
(3)∵x +y =20,xy=8,∴x +y =(x +y ) -2(xy) =20 -2×8 =272.
21.解:如图,
∵点A表示2.4,点B表示-3.6,点C表示-0.6,∴OA=2.4,OB=3.6,OC=0.6.
(1)线段AB=OA+OB=2.4+3.6=6.
(2)点C是线段AB的中点.理由如下:
∵AC=OA+OC=2.4+0.6=3,BC=OB-OC=3.6-0.6=3,∴AC=BC,即C是线段AB的中点.
(3)设D的坐标为x,即BD=CD,则有:(-0.6)-x=x-(-3.6),解得x=-2.1.
∴点D表示的数是-2.1.
22.(1)解:∵AD∥EF,∴∠BAD+∠2=180°.
∵∠1+∠2=180°,∴∠1=∠BAD.
∵∠1=50°,∴∠BAD=50°.
(2)证明:∵DG⊥AC,∴∠DGC=90°.
∵∠BAC=90°,∴∠BAC=∠DGC,∴AB∥DG,∴∠BAD=∠ADG.
由(1)得∠1=∠BAD,∴∠1=∠ADG,∴DG平分∠ADC.
23.解:(1)∵∠AOC=30°,∴∠BOC=180°-∠AOC=150°.
又∵∠COD是直角,OE平分∠BOC,
(2)∠AOC=2∠DOE.理由如下:
∵∠COD是直角,OE平分∠BOC,∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE)=2∠DOE.
(3)∠AOC=360°-2∠DOE.理由如下:
∵OE平分∠BOC,∴∠BOC=2∠COE,
∴∠AOC=180° -∠BOC=180° -2∠COE=180° -2(∠DOE-90°)=360°-2∠DOE.
24.解:(1)本次调查的家长有:30÷15%=200(名),故答案为200.
(2)A类型的扇形圆心角的度数为360°×15%=54°,故答案为54°.
(3)由题意可得,C类型的家长有:200-30-40-120=10(名),补全的折线统计图,如图所示.
(4)由题意,可得 (名),
即该市区18000名中学生家长中有10800名家长持反对态度.
25.解:(1)兔子 乌龟 1500
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50(米),∴乌龟每分钟爬50米.
(3)700÷50=14(分钟),∴乌龟用了14分钟追上了正在睡觉的兔子.
(4)∵48千米=48000米,
∴48000÷60=800(米/分),(1500-700)÷800=1(分钟),30+0.5-1×2=28.5(分钟),
∴兔子中间停下睡觉用了28.5分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
