八年级下册数学期末测试题(二)(含解析)
文档属性
| 名称 | 八年级下册数学期末测试题(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 09:29:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级下册数学期末测试题(二)
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,遵义的红军烈士陵园集中了建国后在遵义各处找到的红军遗骨,故又称红军山,陵园正面是在纪念遵义会议五十周年时兴建的一座别具特色的纪念碑.从山脚一点A到纪念碑底部一点B,沿右边楼梯直行和沿左边弯曲的盘山公路走相比,缩短了行走的路程,其中蕴含的数学道理是 ( )
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.同一平面内垂直于同一条直线的两直线平行
2.下列说法错误的是( )
A.直线经过点A B.直线a,b相交于点A
C.点C在线段AB上 D.射线CD与线段AB有公共点
3.2019新型冠状病毒在2020年1月12日被世界卫生组织命名为2019-nCoV,它的平均直径大约为80~140纳米之间,已知1纳米米,将140纳米用科学记数法可表示为( )
米 米 米 米
4.下列计算正确的是 ( )
5.已知则 的值为( )
A.3 B.8
6.已知线段AB,延长AB到C,使D为AC的中点,若AB=9cm,则DC的长为 ( )
A.5cm B.6 cm C.7 cm D.5.5cm
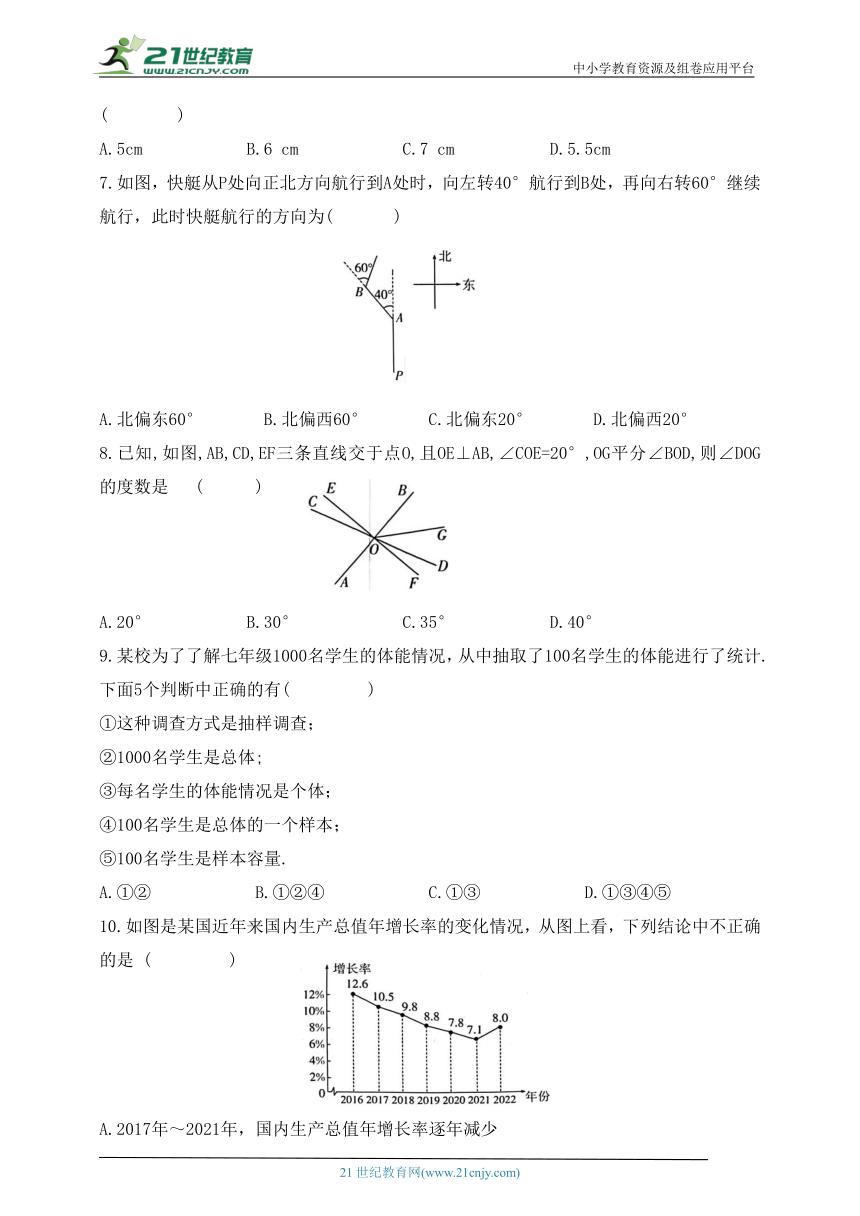
7.如图,快艇从P处向正北方向航行到A处时,向左转40°航行到B处,再向右转60°继续航行,此时快艇航行的方向为( )
A.北偏东60° B.北偏西60° C.北偏东20° D.北偏西20°
8.已知,如图,AB,CD,EF三条直线交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,则∠DOG的度数是 ( )
A.20° B.30° C.35° D.40°
9.某校为了了解七年级1000名学生的体能情况,从中抽取了100名学生的体能进行了统计.下面5个判断中正确的有( )
①这种调查方式是抽样调查;
②1000名学生是总体;
③每名学生的体能情况是个体;
④100名学生是总体的一个样本;
⑤100名学生是样本容量.
A.①② B.①②④ C.①③ D.①③④⑤
10.如图是某国近年来国内生产总值年增长率的变化情况,从图上看,下列结论中不正确的是 ( )
A.2017年~2021年,国内生产总值年增长率逐年减少
B.2022年,国内生产总值的年增长率开始回升
C.这7年中,每年的国内生产总值不断增长
D.这7年中,每年的国内生产总值有增有减
11.瓶子或者罐头盒等圆柱形的物体常常用如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如下表.则下列说法错误的是 ( )
层数n/层 1 2 3 4 5 …
物体总数y/个 1 3 6 10 15 …
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
12.自驾游是当今社会一种重要的旅游方式,五一放假期间玲玲一家人自驾去泰山游玩,如图描述了玲玲爸爸驾驶汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车在0~1小时的速度是60千米/时
B.汽车在2~3小时的速度比0~0.5小时的速度快
C.汽车行驶的平均速度为60千米/时
D.汽车从0.5小时到1.5小时的速度是80千米/时
二、填空题(每小题4分,共24分)
13.已知a+b=2,ab=-7,则(a-2)(b-2)= .
14.若n是正整数,且 则 的值 .
15.如图,∠AOC=90°,OC平分∠DOB,且∠BOA的度数是 .
16.如图,直线l ∥l ,AB⊥EF,∠1=20°,那么∠2= .
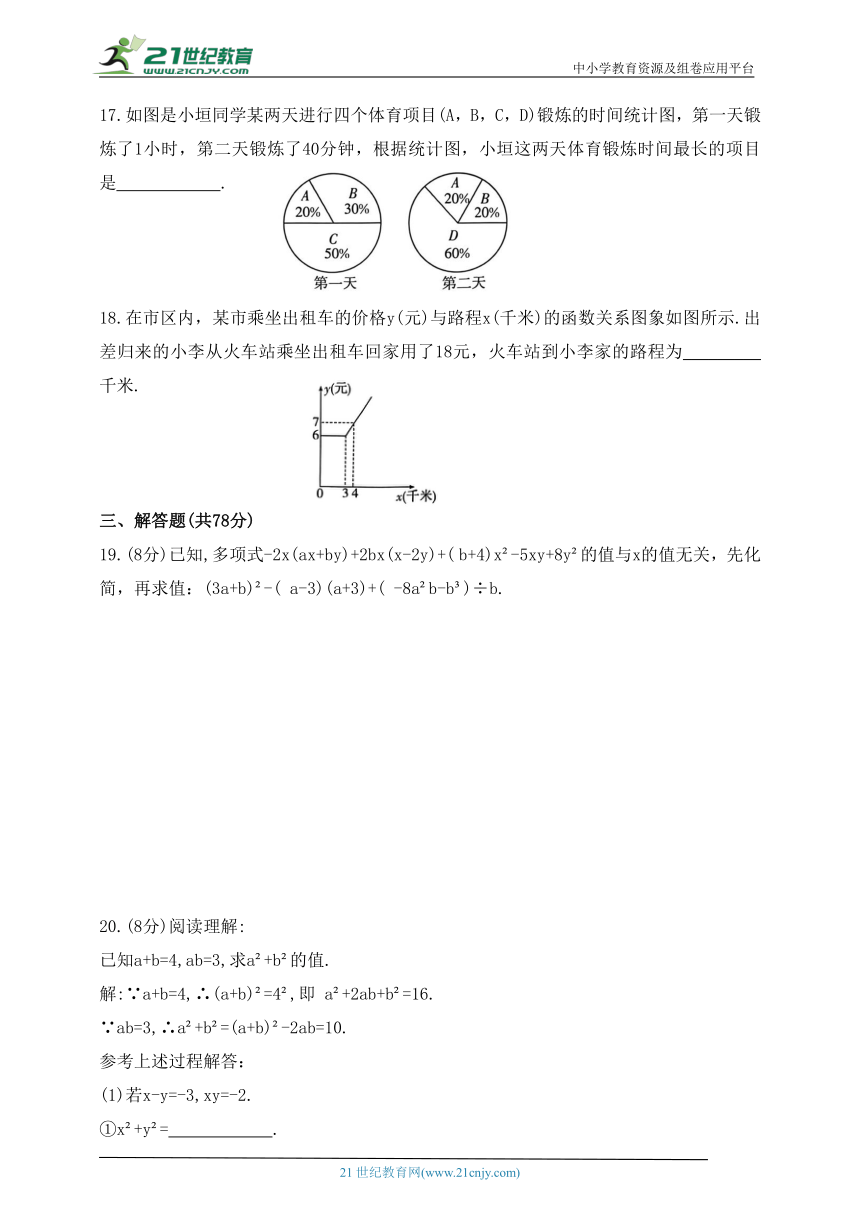
17.如图是小垣同学某两天进行四个体育项目(A,B,C,D)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是 .
18.在市区内,某市乘坐出租车的价格y(元)与路程x(千米)的函数关系图象如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为_________千米.
三、解答题(共78分)
19.(8分)已知,多项式-2x(ax+by)+2bx(x-2y)+( b+4)x -5xy+8y 的值与x的值无关,先化简,再求值:(3a+b) -( a-3)(a+3)+( -8a b-b )÷b.
20.(8分)阅读理解:
已知a+b=4,ab=3,求a +b 的值.
解:∵a+b=4,∴(a+b) =4 ,即 a +2ab+b =16.
∵ab=3,∴a +b =(a+b) -2ab=10.
参考上述过程解答:
(1)若x-y=-3,xy=-2.
①x +y = .
②求(x+y) 的值.
(2)若m+n-p=-10,(m-p)·n=-1,求 (m-p) +n 的值.
21.(10分)如图,已知点A,B,C,D,E在同一直线上,且AC=BD,E是线段BC的中点.
(1)点E是线段AD的中点吗 说明理由.
(2)当AD=10,AB=3时,求线段BE的长度.
22.(10分)如图,直线AB,CD,EF相交于点O,OG⊥CD.
(1)已知∠BOD=36°,求∠AOG的度数.
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗 说明理由.
23.(14分)为更有针对性地开展“学党史志愿服务”活动,某校开展了以“我最想参加的志愿服务小组”为主题的调查活动,围绕在“学习、体育、文艺、科普四个志愿服务小组中,你想参加哪一个小组 (必选且只选一个)”的问题在全校范围内,随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的统计图,其中想参加体育小组的占所调查人数的25%.
根据图中信息解决下列问题:
(1)针对这次调查:
①共抽取了 名学生进行问卷调查.
②想参加文艺小组的有 名学生;
③若绘制扇形统计图,则学习小组的扇形的圆心角为 °.
(2)若该校共有1200名学生,通过计算估计全校想参加科普小组的学生人数.
24.(14分)小华和小明是姐弟俩,某日早晨,小明7:40先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00赶到学校,他们从家到学校已走的路程s (米)和所用时间t(分钟)的关系图如图所示.请结合图中信息解答下列问题:
(1)小明家和学校的距离是 米;小明在广场向行人讲解卫生防疫常识所用的时间是 分钟.
(2)分别求小华的速度和小明从广场跑去学校的速度.
(3)求小华在广场看到小明时是几点几分
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次 (结果保留整数)
25.(14分)已知:AB∥CD,直线EF分别交AB,CD于点E,F,直线GH分别交AB,CD于点G,H.
(1)如图1,若∠BGH=80°,∠BEF=120°,EM平分∠AEF,HM平分∠GHC,求∠EMH的度数.
(2)如图2,HM平分∠GHC,EN平分∠BEF交MH的延长线于点N,探究∠MNE,∠BGH,∠BEF之间的数量关系,并说明理由.
(3)如图3,直线EF,GH交于点P,PQ平分∠FPH,FK 平分∠PFC,过P作PO∥FK,探究∠QPO与∠PHC之间的数量关系,并说明理由.
参考答案
1. B 2. C 3. B 4. B 5. A 6. B 7. C 8. C 9. C 10. D 11. C
12. D【解析】汽车在0~0.5小时的速度是:30÷0.5=60(千米/时),0.5~1.5小时的速度为:(110-30)÷1=80(千米/时),0~1小时的平均速度为:70÷1=70(千米/时),故A错误,不符合题意;汽车在0~0.5小时的速度为:30÷0.5=60(千米/时),2~3小时的速度为:(150-110)÷(3-2)=40(千米/时),所以汽车在2~3小时的速度比0~0.5小时的速度慢,故B错误,不符合题意;汽车行驶的平均速度为:150÷3=50(千米/时),故C错误,不符合题意;汽车从0.5小时到1.5小时的速度为:(110-30)÷(1.5-0.5)=80(千米/时),故D正确,符合题意.故选D.
13.-7
【解析】
【解析】∵OC平分∠DOB,∴∠BOC=∠DOC=22°39'.
∵∠AOC=90° ,∴∠BOA=90° -∠BOC=90° -
16.70° 【解析】如图,作OC∥.∵∥,∴OC∥∥.
∴∠3=∠1,∠2=∠4.∵∠1=20°,∴∠3=∠1=20°.
又∵AB⊥EF,∴∠BOF=90°.∴∠4=90°-∠3=90°-20°=70°.∴∠2=∠4=70°.
17. C 18.15
19.解:
∵代数式的值与x的值无关,
∴,解得
当时,上式
20.解:(1)①∵x-y=-3,∴(x-y) =( -3) ,x -2xy+y =9.
∵xy=-2,∴x +y =(x-y) +2xy=9+2x( -2)=5.
②∵(x+y) =x +2xy+y ,∴(x+y) =5+2×( -2)=5-4=1.
(2)∵m+n-p=-10,∴(m-p+n) =10 ,即 (m-p) +2(m-p) · n+n =100.
∵(m-p) · n=-1,∴(m-p) +n =(m-p+n) -2(m-p) · n=100-2×( -1)=100+2=102.
21.解:(1)点E是线段AD的中点.理由如下:
∵AC=BD,∴AC-BC=BD-BC,即AB=CD.
∵E是线段BC的中点,∴BE=CE,∴AB+BE=CD+CE.
即AE=ED,∴点E是AD的中点.
(2)∵AD=10,AB=3,∴BC=AD-2AB=10-2×3=4,
即线段BE的长度为2.
22.解:(1)∵∠BOD=36°(已知),∴∠AOC=∠BOD=36°(对顶角相等).
∵OG⊥CD(已知),∴∠COG=90°(垂直的定义),即∠AOC+∠AOG=90°,
∴∠AOG=90°-∠AOC=90°-36°=54°.
(2)OG是∠AOF的角平分线.理由如下:
∵OC平分∠AOE(已知),∴∠AOC=∠COE(角平分线的概念).
∵∠COG=90°(已证),∴∠AOC+∠AOG=90°.
∵∠COE+∠AOC+∠AOG+∠GOF=180°(平角的概念),
∴∠COE+∠GOF=90°(等式性质),∴∠AOG=∠GOF(等角的余角相等),
∴OG是∠AOF的角平分线(角平分线的概念).
23.解:(1)①15÷25%=60(名),故答案为:60;
②60-9-15-12=24(名),故答案为:24;
③扇形统计图中,学习类扇形的圆心角的度数是
故答案为:54.
(名),
即估计全校想参加科普小组的学生人数有240名.
24.解:(1)1280 6
(2)小华的速度为:1280÷(20-4)=80(米/分),
小明从广场跑去学校的速度为:
(1280-560)÷(20-14)=120(米/分).
(3)560÷80=7(分),40+4+7=51(分),
∴小华在广场看到小明时是7:51.
(分), (分),
∴在保证不迟到的情况下,小明最多可以讲解1次.
25.解:(1)如图1,过点M作MN∥AB.
∵AB∥CD,∴MN∥AB∥CD, ∴∠BGH=∠GHC=80°.
∵HM平分∠GHC,
∵∠BEF=120°,∴∠AEF=60°.
∵EM平分∠AEF,
∵MN∥AB∥CD,∴∠EMN=∠AEM=30°,∠HMN=∠MHC=40°,
∴∠EMH=∠EMN+∠HMN=30°+40°=70°.
理由如下:
如图2,过点N作NK∥CD.
∵AB∥CD,∴NK∥AB,∴∠ENK=∠BEN.
∵EN平分∠BEF.
∵NK∥CD,∴∠MHC=∠MNK.
∵HM平分∠GHC,
又∵AB∥CD,∴∠BGH=∠GHC,
∴∠MNE=∠ENK-∠MNK,
理由如下:
如图3,过点F作FS∥PH.
∵FS∥PH,∴∠PFS=∠FPH.
∵PQ平分∠FPH,∴∠FPH=2∠FPQ,∴∠PFS=2∠FPQ.
又∵FS∥PH,∴∠CFS=∠PHC,
∴∠PFC=∠CFS+∠PFS=∠PHC+2∠FPQ.
∵FK平分∠PFC,
∵PO∥FK,∴∠PFK=∠FPO.
∵∠QPO=∠FPO-∠FPQ,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
八年级下册数学期末测试题(二)
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,遵义的红军烈士陵园集中了建国后在遵义各处找到的红军遗骨,故又称红军山,陵园正面是在纪念遵义会议五十周年时兴建的一座别具特色的纪念碑.从山脚一点A到纪念碑底部一点B,沿右边楼梯直行和沿左边弯曲的盘山公路走相比,缩短了行走的路程,其中蕴含的数学道理是 ( )
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.同一平面内垂直于同一条直线的两直线平行
2.下列说法错误的是( )
A.直线经过点A B.直线a,b相交于点A
C.点C在线段AB上 D.射线CD与线段AB有公共点
3.2019新型冠状病毒在2020年1月12日被世界卫生组织命名为2019-nCoV,它的平均直径大约为80~140纳米之间,已知1纳米米,将140纳米用科学记数法可表示为( )
米 米 米 米
4.下列计算正确的是 ( )
5.已知则 的值为( )
A.3 B.8
6.已知线段AB,延长AB到C,使D为AC的中点,若AB=9cm,则DC的长为 ( )
A.5cm B.6 cm C.7 cm D.5.5cm
7.如图,快艇从P处向正北方向航行到A处时,向左转40°航行到B处,再向右转60°继续航行,此时快艇航行的方向为( )
A.北偏东60° B.北偏西60° C.北偏东20° D.北偏西20°
8.已知,如图,AB,CD,EF三条直线交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,则∠DOG的度数是 ( )
A.20° B.30° C.35° D.40°
9.某校为了了解七年级1000名学生的体能情况,从中抽取了100名学生的体能进行了统计.下面5个判断中正确的有( )
①这种调查方式是抽样调查;
②1000名学生是总体;
③每名学生的体能情况是个体;
④100名学生是总体的一个样本;
⑤100名学生是样本容量.
A.①② B.①②④ C.①③ D.①③④⑤
10.如图是某国近年来国内生产总值年增长率的变化情况,从图上看,下列结论中不正确的是 ( )
A.2017年~2021年,国内生产总值年增长率逐年减少
B.2022年,国内生产总值的年增长率开始回升
C.这7年中,每年的国内生产总值不断增长
D.这7年中,每年的国内生产总值有增有减
11.瓶子或者罐头盒等圆柱形的物体常常用如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如下表.则下列说法错误的是 ( )
层数n/层 1 2 3 4 5 …
物体总数y/个 1 3 6 10 15 …
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
12.自驾游是当今社会一种重要的旅游方式,五一放假期间玲玲一家人自驾去泰山游玩,如图描述了玲玲爸爸驾驶汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )
A.汽车在0~1小时的速度是60千米/时
B.汽车在2~3小时的速度比0~0.5小时的速度快
C.汽车行驶的平均速度为60千米/时
D.汽车从0.5小时到1.5小时的速度是80千米/时
二、填空题(每小题4分,共24分)
13.已知a+b=2,ab=-7,则(a-2)(b-2)= .
14.若n是正整数,且 则 的值 .
15.如图,∠AOC=90°,OC平分∠DOB,且∠BOA的度数是 .
16.如图,直线l ∥l ,AB⊥EF,∠1=20°,那么∠2= .
17.如图是小垣同学某两天进行四个体育项目(A,B,C,D)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是 .
18.在市区内,某市乘坐出租车的价格y(元)与路程x(千米)的函数关系图象如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为_________千米.
三、解答题(共78分)
19.(8分)已知,多项式-2x(ax+by)+2bx(x-2y)+( b+4)x -5xy+8y 的值与x的值无关,先化简,再求值:(3a+b) -( a-3)(a+3)+( -8a b-b )÷b.
20.(8分)阅读理解:
已知a+b=4,ab=3,求a +b 的值.
解:∵a+b=4,∴(a+b) =4 ,即 a +2ab+b =16.
∵ab=3,∴a +b =(a+b) -2ab=10.
参考上述过程解答:
(1)若x-y=-3,xy=-2.
①x +y = .
②求(x+y) 的值.
(2)若m+n-p=-10,(m-p)·n=-1,求 (m-p) +n 的值.
21.(10分)如图,已知点A,B,C,D,E在同一直线上,且AC=BD,E是线段BC的中点.
(1)点E是线段AD的中点吗 说明理由.
(2)当AD=10,AB=3时,求线段BE的长度.
22.(10分)如图,直线AB,CD,EF相交于点O,OG⊥CD.
(1)已知∠BOD=36°,求∠AOG的度数.
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗 说明理由.
23.(14分)为更有针对性地开展“学党史志愿服务”活动,某校开展了以“我最想参加的志愿服务小组”为主题的调查活动,围绕在“学习、体育、文艺、科普四个志愿服务小组中,你想参加哪一个小组 (必选且只选一个)”的问题在全校范围内,随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的统计图,其中想参加体育小组的占所调查人数的25%.
根据图中信息解决下列问题:
(1)针对这次调查:
①共抽取了 名学生进行问卷调查.
②想参加文艺小组的有 名学生;
③若绘制扇形统计图,则学习小组的扇形的圆心角为 °.
(2)若该校共有1200名学生,通过计算估计全校想参加科普小组的学生人数.
24.(14分)小华和小明是姐弟俩,某日早晨,小明7:40先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00赶到学校,他们从家到学校已走的路程s (米)和所用时间t(分钟)的关系图如图所示.请结合图中信息解答下列问题:
(1)小明家和学校的距离是 米;小明在广场向行人讲解卫生防疫常识所用的时间是 分钟.
(2)分别求小华的速度和小明从广场跑去学校的速度.
(3)求小华在广场看到小明时是几点几分
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次 (结果保留整数)
25.(14分)已知:AB∥CD,直线EF分别交AB,CD于点E,F,直线GH分别交AB,CD于点G,H.
(1)如图1,若∠BGH=80°,∠BEF=120°,EM平分∠AEF,HM平分∠GHC,求∠EMH的度数.
(2)如图2,HM平分∠GHC,EN平分∠BEF交MH的延长线于点N,探究∠MNE,∠BGH,∠BEF之间的数量关系,并说明理由.
(3)如图3,直线EF,GH交于点P,PQ平分∠FPH,FK 平分∠PFC,过P作PO∥FK,探究∠QPO与∠PHC之间的数量关系,并说明理由.
参考答案
1. B 2. C 3. B 4. B 5. A 6. B 7. C 8. C 9. C 10. D 11. C
12. D【解析】汽车在0~0.5小时的速度是:30÷0.5=60(千米/时),0.5~1.5小时的速度为:(110-30)÷1=80(千米/时),0~1小时的平均速度为:70÷1=70(千米/时),故A错误,不符合题意;汽车在0~0.5小时的速度为:30÷0.5=60(千米/时),2~3小时的速度为:(150-110)÷(3-2)=40(千米/时),所以汽车在2~3小时的速度比0~0.5小时的速度慢,故B错误,不符合题意;汽车行驶的平均速度为:150÷3=50(千米/时),故C错误,不符合题意;汽车从0.5小时到1.5小时的速度为:(110-30)÷(1.5-0.5)=80(千米/时),故D正确,符合题意.故选D.
13.-7
【解析】
【解析】∵OC平分∠DOB,∴∠BOC=∠DOC=22°39'.
∵∠AOC=90° ,∴∠BOA=90° -∠BOC=90° -
16.70° 【解析】如图,作OC∥.∵∥,∴OC∥∥.
∴∠3=∠1,∠2=∠4.∵∠1=20°,∴∠3=∠1=20°.
又∵AB⊥EF,∴∠BOF=90°.∴∠4=90°-∠3=90°-20°=70°.∴∠2=∠4=70°.
17. C 18.15
19.解:
∵代数式的值与x的值无关,
∴,解得
当时,上式
20.解:(1)①∵x-y=-3,∴(x-y) =( -3) ,x -2xy+y =9.
∵xy=-2,∴x +y =(x-y) +2xy=9+2x( -2)=5.
②∵(x+y) =x +2xy+y ,∴(x+y) =5+2×( -2)=5-4=1.
(2)∵m+n-p=-10,∴(m-p+n) =10 ,即 (m-p) +2(m-p) · n+n =100.
∵(m-p) · n=-1,∴(m-p) +n =(m-p+n) -2(m-p) · n=100-2×( -1)=100+2=102.
21.解:(1)点E是线段AD的中点.理由如下:
∵AC=BD,∴AC-BC=BD-BC,即AB=CD.
∵E是线段BC的中点,∴BE=CE,∴AB+BE=CD+CE.
即AE=ED,∴点E是AD的中点.
(2)∵AD=10,AB=3,∴BC=AD-2AB=10-2×3=4,
即线段BE的长度为2.
22.解:(1)∵∠BOD=36°(已知),∴∠AOC=∠BOD=36°(对顶角相等).
∵OG⊥CD(已知),∴∠COG=90°(垂直的定义),即∠AOC+∠AOG=90°,
∴∠AOG=90°-∠AOC=90°-36°=54°.
(2)OG是∠AOF的角平分线.理由如下:
∵OC平分∠AOE(已知),∴∠AOC=∠COE(角平分线的概念).
∵∠COG=90°(已证),∴∠AOC+∠AOG=90°.
∵∠COE+∠AOC+∠AOG+∠GOF=180°(平角的概念),
∴∠COE+∠GOF=90°(等式性质),∴∠AOG=∠GOF(等角的余角相等),
∴OG是∠AOF的角平分线(角平分线的概念).
23.解:(1)①15÷25%=60(名),故答案为:60;
②60-9-15-12=24(名),故答案为:24;
③扇形统计图中,学习类扇形的圆心角的度数是
故答案为:54.
(名),
即估计全校想参加科普小组的学生人数有240名.
24.解:(1)1280 6
(2)小华的速度为:1280÷(20-4)=80(米/分),
小明从广场跑去学校的速度为:
(1280-560)÷(20-14)=120(米/分).
(3)560÷80=7(分),40+4+7=51(分),
∴小华在广场看到小明时是7:51.
(分), (分),
∴在保证不迟到的情况下,小明最多可以讲解1次.
25.解:(1)如图1,过点M作MN∥AB.
∵AB∥CD,∴MN∥AB∥CD, ∴∠BGH=∠GHC=80°.
∵HM平分∠GHC,
∵∠BEF=120°,∴∠AEF=60°.
∵EM平分∠AEF,
∵MN∥AB∥CD,∴∠EMN=∠AEM=30°,∠HMN=∠MHC=40°,
∴∠EMH=∠EMN+∠HMN=30°+40°=70°.
理由如下:
如图2,过点N作NK∥CD.
∵AB∥CD,∴NK∥AB,∴∠ENK=∠BEN.
∵EN平分∠BEF.
∵NK∥CD,∴∠MHC=∠MNK.
∵HM平分∠GHC,
又∵AB∥CD,∴∠BGH=∠GHC,
∴∠MNE=∠ENK-∠MNK,
理由如下:
如图3,过点F作FS∥PH.
∵FS∥PH,∴∠PFS=∠FPH.
∵PQ平分∠FPH,∴∠FPH=2∠FPQ,∴∠PFS=2∠FPQ.
又∵FS∥PH,∴∠CFS=∠PHC,
∴∠PFC=∠CFS+∠PFS=∠PHC+2∠FPQ.
∵FK平分∠PFC,
∵PO∥FK,∴∠PFK=∠FPO.
∵∠QPO=∠FPO-∠FPQ,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
