数学人教A版(2019)必修第二册6.3.1平面向量基本定理 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.3.1平面向量基本定理 课件(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 34.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-19 21:48:04 | ||
图片预览






文档简介
(共26张PPT)
6.3.1
平面向量基本定理
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
学习目标
平面向量基本定理
1
平面向量基本定理应用
2
课堂小结
3
课后作业
4
PART.01
平面向量基本定理
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
平面向量基本定理
动人的旋律由基本音符Do,Re,Mi,Fa,So,La,Si组成
绚丽的色彩由红、黄、蓝三原色组成
在多样的向量世界中我们能否找到基本组成元素?
平面向量基本定理
我们知道,已知两个力,可以求出它们的合力;反过来,一个力也可以分解为两个力。
我们可以根据解决问题实际问题的需要,通过作平行四边形,将力F分解为多组大小、方向不同的分力。
。
平面向量基本定理
由力的分解得到启发,我们能否通过作平行四边形,将向量 分解为两个向量,使向量 是这两个向量的和呢?
平面向量基本定理
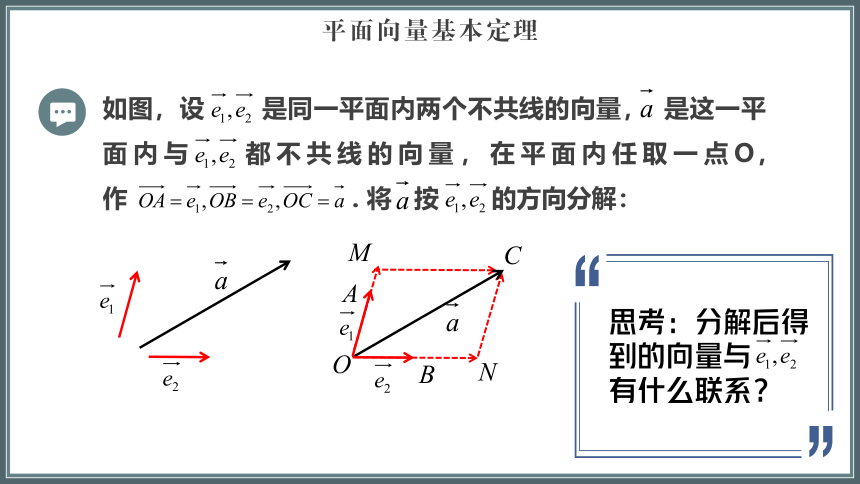
如图,设 是同一平面内两个不共线的向量, 是这一平面内与 都不共线的向量,在平面内任取一点O,作 . 将 按 的方向分解:
思考:分解后得到的向量与
有什么联系?
平面向量基本定理
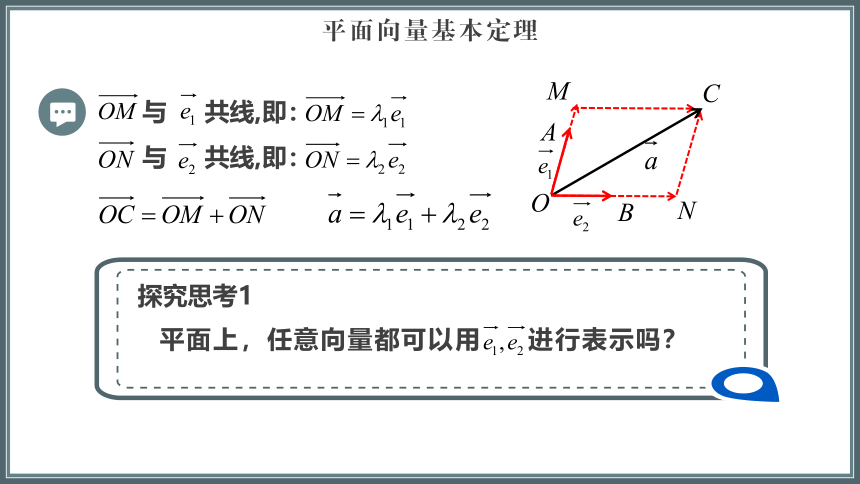
与 共线,即:
与 共线,即:
平面上,任意向量都可以用 进行表示吗?
探究思考1
平面向量基本定理
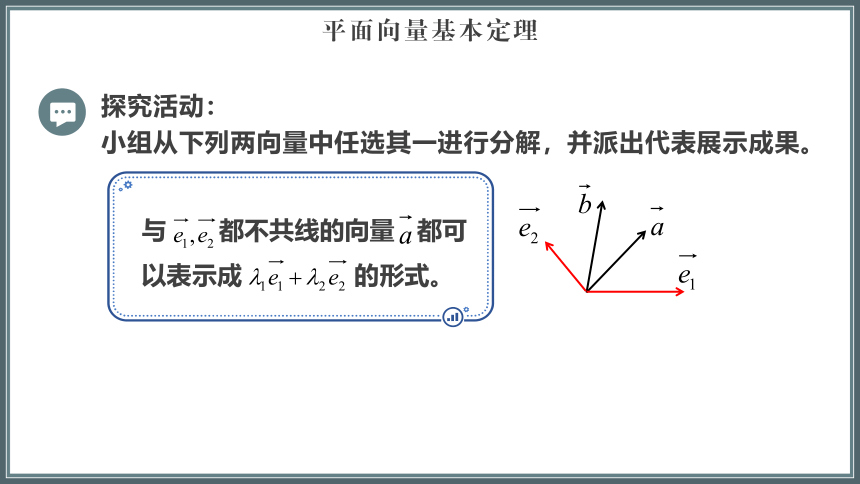
探究活动:
小组从下列两向量中任选其一进行分解,并派出代表展示成果。
与 都不共线的向量 都可以表示成 的形式。
平面向量基本定理
是与 或 共线的非零向量时 成立吗?
探究思考2
是与 共线的非零向量时 成立.
是与 共线的非零向量时 成立.
平面向量基本定理
是零向量时 成立吗?
探究思考3
是零向量时 成立.
平面向量基本定理
探究思考4
平面内任何一个向量 都可以表示成 的形式,那么这种表示是唯一的吗?(即 的系数是唯一的吗?)
平面向量基本定理
假设: ,
即
假设 不全为0,不妨设
则
由此可得 共线,与已知 不共线矛盾
则 全为0,即
所以表示形式是唯一的。
平面向量基本定理
如果 是同一平面内的两个 向量,那么对于这一平面内的任意向量 , 一对实数 ,使
不共线
有且只有
平面向量基本定理
基底:
若 不共线,我们把{ }叫做表示这一平面内所有向量的一个基底。
思考:平面向量基本定理中有哪些关键需要注意
PART.02
平面向量基本定理的应用
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
平面向量基本定理的应用
(多选)设{ }是平面内所有向量的一个基底,则下列四组向量中,能作为基底的是( )
A. 和
B. 和
C. 和
D. 和
ACD
平面向量基本定理的应用
如图, 不共线,且M为AB的中点,用 来表示 .
动手挑战并大胆分享你的求解思路
平面向量基本定理的应用
如图, 不共线,且E、F为AB的三等分点,用 来表示 .
平面向量基本定理的应用
如图, 不共线,且 ,用 来表示 .
类比思考:
平面向量基本定理的应用
思考探究:
如果A,B,C三点共线,点O是平面内任意一点,若 ,则 之间具有怎样的数量关系?
如果A,B,C三点共线,点O是平面内任意一点,若 ,则
平面向量基本定理的应用
例题解析:
如图,CD是△ABC的中线,且CD=AB,用向量方法证明△ABC是直角三角形。
证明:如图,设
则
于是△ABC是直角三角形。
PART.03
课堂小结
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
课堂小结
思想分享
知识分享
分享你在本堂课中的收获
方法分享
其它分享
PART.04
课后作业
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
课后作业
教材27页
练习1,2,3
教材36页
习题6.3 1
祝各位同学学习进步
—— END ——
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
6.3.1
平面向量基本定理
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
学习目标
平面向量基本定理
1
平面向量基本定理应用
2
课堂小结
3
课后作业
4
PART.01
平面向量基本定理
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
平面向量基本定理
动人的旋律由基本音符Do,Re,Mi,Fa,So,La,Si组成
绚丽的色彩由红、黄、蓝三原色组成
在多样的向量世界中我们能否找到基本组成元素?
平面向量基本定理
我们知道,已知两个力,可以求出它们的合力;反过来,一个力也可以分解为两个力。
我们可以根据解决问题实际问题的需要,通过作平行四边形,将力F分解为多组大小、方向不同的分力。
。
平面向量基本定理
由力的分解得到启发,我们能否通过作平行四边形,将向量 分解为两个向量,使向量 是这两个向量的和呢?
平面向量基本定理
如图,设 是同一平面内两个不共线的向量, 是这一平面内与 都不共线的向量,在平面内任取一点O,作 . 将 按 的方向分解:
思考:分解后得到的向量与
有什么联系?
平面向量基本定理
与 共线,即:
与 共线,即:
平面上,任意向量都可以用 进行表示吗?
探究思考1
平面向量基本定理
探究活动:
小组从下列两向量中任选其一进行分解,并派出代表展示成果。
与 都不共线的向量 都可以表示成 的形式。
平面向量基本定理
是与 或 共线的非零向量时 成立吗?
探究思考2
是与 共线的非零向量时 成立.
是与 共线的非零向量时 成立.
平面向量基本定理
是零向量时 成立吗?
探究思考3
是零向量时 成立.
平面向量基本定理
探究思考4
平面内任何一个向量 都可以表示成 的形式,那么这种表示是唯一的吗?(即 的系数是唯一的吗?)
平面向量基本定理
假设: ,
即
假设 不全为0,不妨设
则
由此可得 共线,与已知 不共线矛盾
则 全为0,即
所以表示形式是唯一的。
平面向量基本定理
如果 是同一平面内的两个 向量,那么对于这一平面内的任意向量 , 一对实数 ,使
不共线
有且只有
平面向量基本定理
基底:
若 不共线,我们把{ }叫做表示这一平面内所有向量的一个基底。
思考:平面向量基本定理中有哪些关键需要注意
PART.02
平面向量基本定理的应用
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
平面向量基本定理的应用
(多选)设{ }是平面内所有向量的一个基底,则下列四组向量中,能作为基底的是( )
A. 和
B. 和
C. 和
D. 和
ACD
平面向量基本定理的应用
如图, 不共线,且M为AB的中点,用 来表示 .
动手挑战并大胆分享你的求解思路
平面向量基本定理的应用
如图, 不共线,且E、F为AB的三等分点,用 来表示 .
平面向量基本定理的应用
如图, 不共线,且 ,用 来表示 .
类比思考:
平面向量基本定理的应用
思考探究:
如果A,B,C三点共线,点O是平面内任意一点,若 ,则 之间具有怎样的数量关系?
如果A,B,C三点共线,点O是平面内任意一点,若 ,则
平面向量基本定理的应用
例题解析:
如图,CD是△ABC的中线,且CD=AB,用向量方法证明△ABC是直角三角形。
证明:如图,设
则
于是△ABC是直角三角形。
PART.03
课堂小结
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
课堂小结
思想分享
知识分享
分享你在本堂课中的收获
方法分享
其它分享
PART.04
课后作业
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
课后作业
教材27页
练习1,2,3
教材36页
习题6.3 1
祝各位同学学习进步
—— END ——
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
