人教A版2019选修一 2.1.1 直线的倾斜角与斜率 课件(共22张PPT)
文档属性
| 名称 | 人教A版2019选修一 2.1.1 直线的倾斜角与斜率 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-19 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
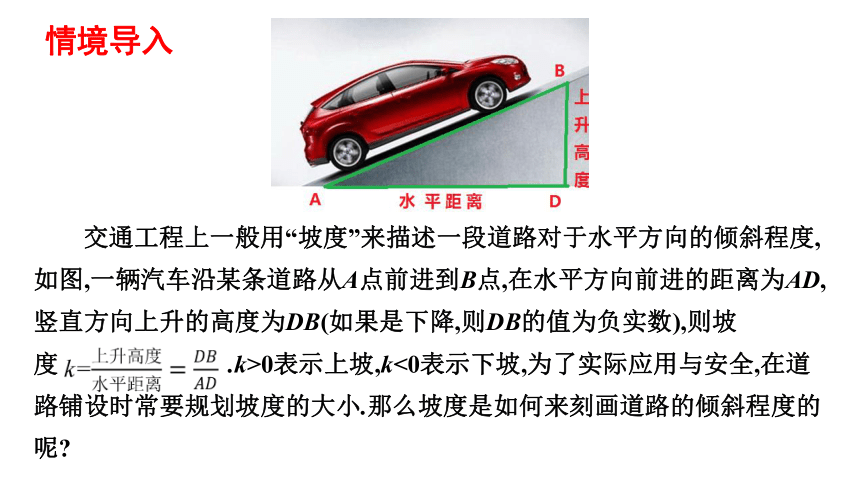
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.那么坡度是如何来刻画道路的倾斜程度的呢
情境导入
直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线
2.1.1 倾斜角与斜率
第二章 §2.1 直线的倾斜角与斜率
问题:确定一条直线的几何要素是什么
思考:
复习引入
y
x
l
O
A
B
O
P
x
y
l1
l2
l3
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
探究新知
1.方向
追问:这些直线的区别是它们的方向不同.如何表示这些直线的方向?
探究新知
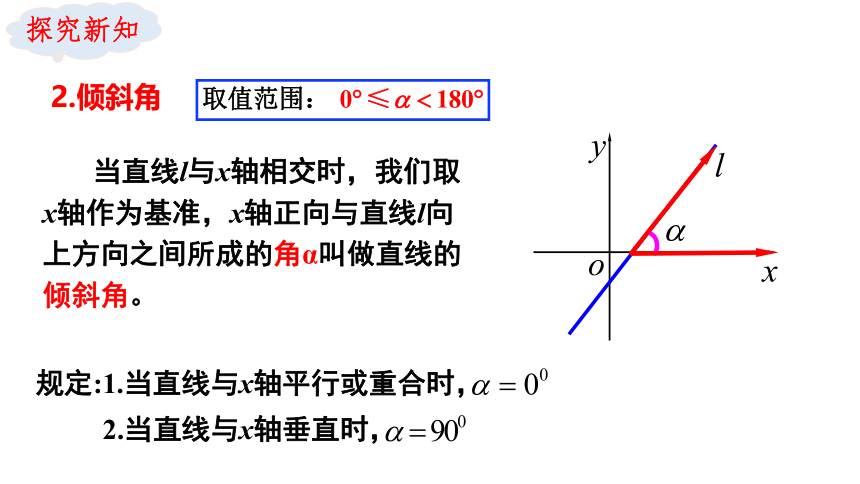
2.倾斜角
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线的
倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
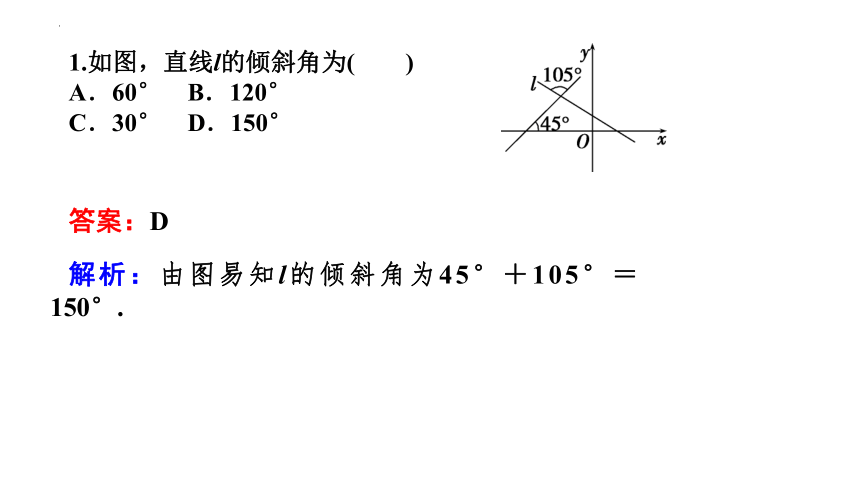
1.如图,直线l的倾斜角为( )
A.60° B.120°
C.30° D.150°
解析:由图易知l的倾斜角为45°+105°=150°.
答案:D
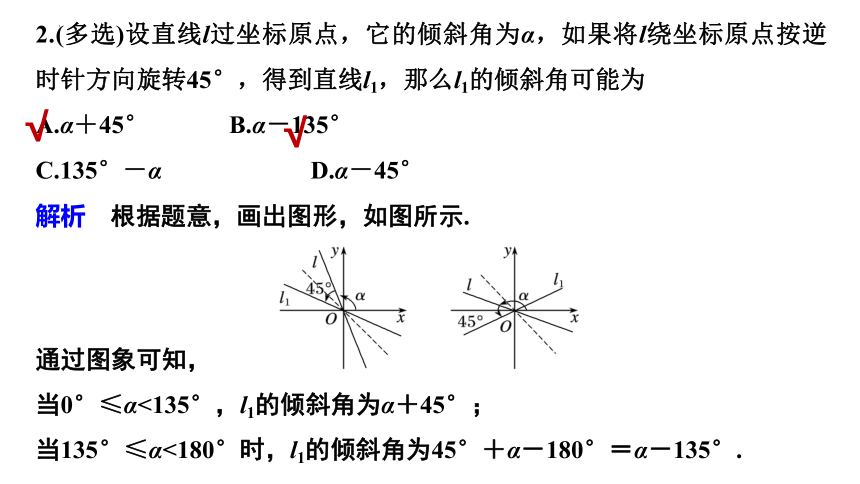
2.(多选)设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角可能为
A.α+45° B.α-135°
C.135°-α D.α-45°
√
√
解析 根据题意,画出图形,如图所示.
通过图象可知,
当0°≤α<135°,l1的倾斜角为α+45°;
当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.
下面我们进一步研究刻画直线倾斜程度的方法.
探究新知
O
x
y
3.倾斜角的正切值
O
x
y
P
P
O
x
y
P1
P2
O
x
y
P2
P1
P
P
O
x
y
P2
P1
O
x
y
P1
P2
P
探究新知
4. 斜率
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度.
5.直线上任意两点纵横坐标的差商
直线的斜率与P1和P2的顺序无关
追问:1.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,所以k =0 .
追问:2.当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:α=90°,斜率不存在,因为分母为0.
书P54 例1
斜率与倾斜角的对应关系
图示
倾斜角 α=0° 0°<α<90° 90°<α<180°
斜率 k>0 不存在
α=90°
k<0
0
当α∈[00, 900)
时,k随α增大
而增大, 且k≥0;
当α∈(900, 1800)
时,k随α增大而增
大,且k<0;
练习1 若45°≤ ≤135°, 则斜率k的取值范围为______________.
练习2 若-1≤k≤1, 则倾斜角 的取值范围为_________________.
[0°, 45°]∪[135°, 180°)
(-∞, -1]∪[1, +∞)
O
3.已知点A(2,3),B(-3,-2),若直线l过点P(1,1),且与线段AB始终没有交点,则直线l的斜率k的取值范围是
√
6.直线的方向向量
1.直线的倾斜角定义及其范围:
2.直线的斜率定义:
3.斜率公式:
课堂小结
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.那么坡度是如何来刻画道路的倾斜程度的呢
情境导入
直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线
2.1.1 倾斜角与斜率
第二章 §2.1 直线的倾斜角与斜率
问题:确定一条直线的几何要素是什么
思考:
复习引入
y
x
l
O
A
B
O
P
x
y
l1
l2
l3
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
探究新知
1.方向
追问:这些直线的区别是它们的方向不同.如何表示这些直线的方向?
探究新知
2.倾斜角
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线的
倾斜角。
规定:1.当直线与x轴平行或重合时,
2.当直线与x轴垂直时,
1.如图,直线l的倾斜角为( )
A.60° B.120°
C.30° D.150°
解析:由图易知l的倾斜角为45°+105°=150°.
答案:D
2.(多选)设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角可能为
A.α+45° B.α-135°
C.135°-α D.α-45°
√
√
解析 根据题意,画出图形,如图所示.
通过图象可知,
当0°≤α<135°,l1的倾斜角为α+45°;
当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.
下面我们进一步研究刻画直线倾斜程度的方法.
探究新知
O
x
y
3.倾斜角的正切值
O
x
y
P
P
O
x
y
P1
P2
O
x
y
P2
P1
P
P
O
x
y
P2
P1
O
x
y
P1
P2
P
探究新知
4. 斜率
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度.
5.直线上任意两点纵横坐标的差商
直线的斜率与P1和P2的顺序无关
追问:1.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,所以k =0 .
追问:2.当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:α=90°,斜率不存在,因为分母为0.
书P54 例1
斜率与倾斜角的对应关系
图示
倾斜角 α=0° 0°<α<90° 90°<α<180°
斜率 k>0 不存在
α=90°
k<0
0
当α∈[00, 900)
时,k随α增大
而增大, 且k≥0;
当α∈(900, 1800)
时,k随α增大而增
大,且k<0;
练习1 若45°≤ ≤135°, 则斜率k的取值范围为______________.
练习2 若-1≤k≤1, 则倾斜角 的取值范围为_________________.
[0°, 45°]∪[135°, 180°)
(-∞, -1]∪[1, +∞)
O
3.已知点A(2,3),B(-3,-2),若直线l过点P(1,1),且与线段AB始终没有交点,则直线l的斜率k的取值范围是
√
6.直线的方向向量
1.直线的倾斜角定义及其范围:
2.直线的斜率定义:
3.斜率公式:
课堂小结
