人教A版(2019)选择性必修第二册 错位相减法求和(教学设计)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 错位相减法求和(教学设计) |  | |
| 格式 | doc | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 08:38:14 | ||
图片预览

文档简介
《错位相减法求和》教学设计
一、目标分析
1.知识目标 使学生掌握等差、等比数列求通项的基本方法,掌握错位相减法求和,熟练解决数列中与错位相减法相关的综合问题。
2.能力目标 培养学生观察、归纳能力,在学习过程中,体会归纳思想、化归思想和方程思想并加深认识;通过等差、等比数列、通项与前n项和关系以及错位相减法之间的综合问题的探究,培养学生分析探索能力,增强运用公式解决综合问题的能力等.
3.情感目标 通过微视频引导学生经历直观感知、类比、转化,实际操作等交流探索活动,使学生经历数学思维的过程, 激发学生的学习兴趣,培养学生勤于思考,善于自主学习的良好习惯。小组合作,分享成功的快乐,体会集体力量的强大。.
二、教学重点、难点
重点 等差等比数列公式的灵活运用,错位相减法求和。
难点 数列相关知识与错位相减法求和间的综合应用。
三、教学模式与教法、学法 采用观看微视频,问题启发、类比、归纳总结相结合的教学方法,让学生掌握并灵活应用错位相减法求和解决数列综合问题。
教师的教法 翻转课堂教学法.
学生的学法 自主学习微视频,积极主动探究,效果检测,合作交流展示,。
四、教具:投影仪、多媒体课件。
五、教学环节
(一)A课成果展示 ,分享收获 (二)B课课标解读,知识梳理 (三)效果检测,合作探究 (四)分组展示,小结反思
六、教学过程
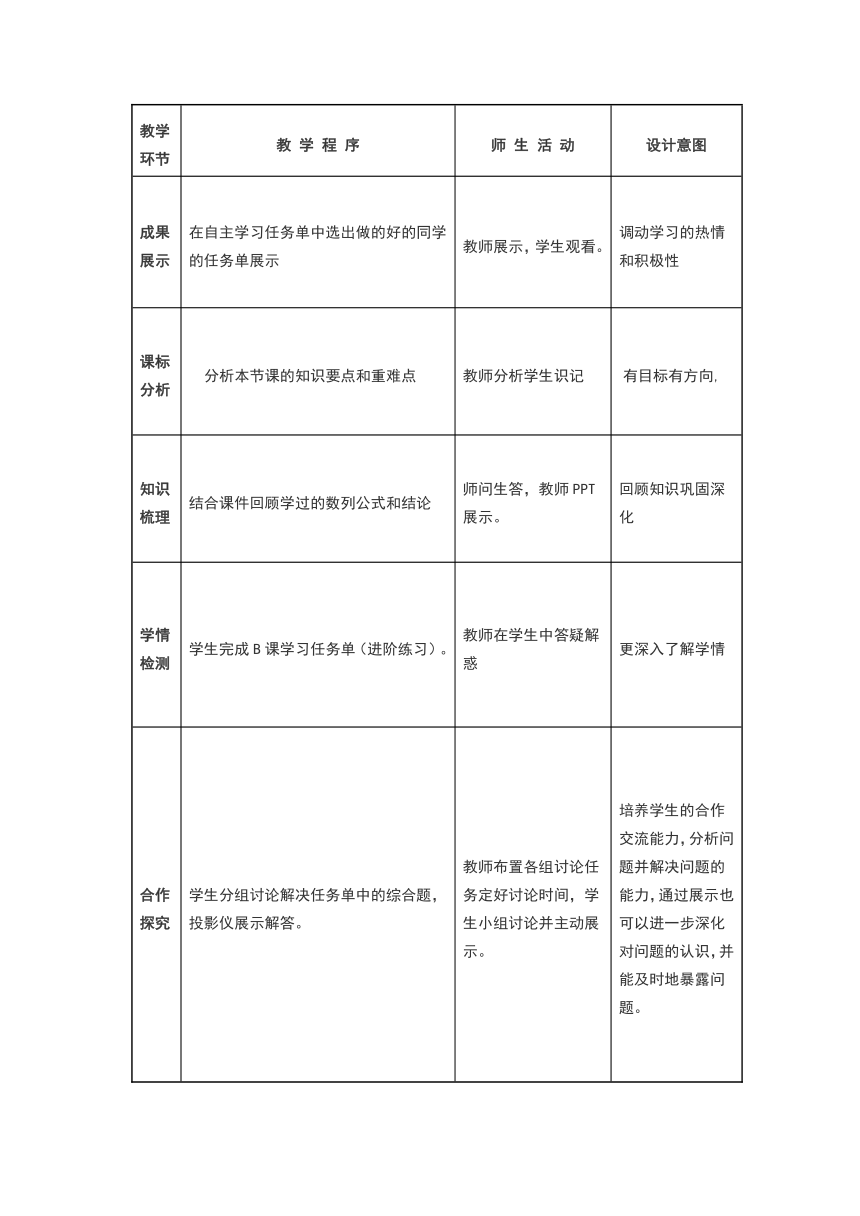
教学环节 教 学 程 序 师 生 活 动 设计意图
成果展示 在自主学习任务单中选出做的好的同学的任务单展示 教师展示,学生观看。 调动学习的热情和积极性
课标分析 分析本节课的知识要点和重难点 教师分析学生识记 有目标有方向,
知识梳理 结合课件回顾学过的数列公式和结论 师问生答,教师PPT展示。 回顾知识巩固深化
学情检测 学生完成B课学习任务单(进阶练习)。 教师在学生中答疑解惑 更深入了解学情
合作探究 学生分组讨论解决任务单中的综合题,投影仪展示解答。 教师布置各组讨论任务定好讨论时间,学生小组讨论并主动展示。 培养学生的合作交流能力,分析问题并解决问题的能力,通过展示也可以进一步深化对问题的认识,并能及时地暴露问题。
进阶练习 题型一 分类讨论求前n项和1.求数列 {nxn} 的前n项和 题型二 等差、等比数列与错位相减法求和 题型三 通项与前n项和的关系以及错位相减法求和3.已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.(1)求an,bn;(2)求数列{an·bn}的前n项和Tn.挑战高考 组(1)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导。组(2)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导,并PPT展示。组(3)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导,并PPT展示详细求解过程。学生自主探索,合作交流。组(4)学生代表投影展示过程。大家一起规范纠错。教师规范解题步骤。 引导学生动手实践,体会不同类型的数列其不同的求和方法的解题策略。培养学生用分类讨论的数学思想来思考问题. 深化学生对错位相减法求和的认识。知识适当的综合培养观察归纳等能力。培养学生严谨的语言表达能力和方程思想。进一步巩固深化知识和方法。让学生感受到综合题其实由单个基本问题通过不同方式结合而成。关键在于探寻知识间的迁移点,化归思想是解决问题的重要途径。亲临考题最前线,激发学生斗志,调动学生学习积极性,主动性。
小结反思归纳总结 【课堂总结】这节课主要学习哪种求和方法 这种求和方法在哪些题型中体现?体会到了哪些数学思想方法?反思 教师引导学生自主完成知识、思想方法的总结。 通过反思与小结使学生对本节课的知识有一个系统全面的认识。数学思想方法是数学的灵魂,引导学生自主完成类比、化归、分类讨论、方程等思想方法的总结,从而更好的理解数学的本质。
布 置 作 业 [课后反馈]课后作业:评测练习1、数列{an}中,a1=2,an+1=an+cn(c是不为零的常数,n=1,2,3,…),且a1,a2,a3成等比数列.(1)求c的值;(2)求{an}的通项公式;(3)求数列的前n项之和Tn.2、已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.(1)求an;(2)求数列{nan}的前n项和Tn.3、已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3).(1)求数列{an}的通项公式;(2)设bn=,求数列{bn}的前n项和Tn;(3)在(2)的条件下,对任意n∈N*,Tn>都成立,求整数m的最大值. 课后完成进一步巩固,深化理解。 学生课后自主完成。 巩固本节知识,培养学生积极主动、勇于探索的精神。
七、板书设计:
1 错位相减法2.等差数列的通项公式和求和公式
3.等比数列的通项公式和求和公式4.通项与前n项和关系
八、教学反思:
一、目标分析
1.知识目标 使学生掌握等差、等比数列求通项的基本方法,掌握错位相减法求和,熟练解决数列中与错位相减法相关的综合问题。
2.能力目标 培养学生观察、归纳能力,在学习过程中,体会归纳思想、化归思想和方程思想并加深认识;通过等差、等比数列、通项与前n项和关系以及错位相减法之间的综合问题的探究,培养学生分析探索能力,增强运用公式解决综合问题的能力等.
3.情感目标 通过微视频引导学生经历直观感知、类比、转化,实际操作等交流探索活动,使学生经历数学思维的过程, 激发学生的学习兴趣,培养学生勤于思考,善于自主学习的良好习惯。小组合作,分享成功的快乐,体会集体力量的强大。.
二、教学重点、难点
重点 等差等比数列公式的灵活运用,错位相减法求和。
难点 数列相关知识与错位相减法求和间的综合应用。
三、教学模式与教法、学法 采用观看微视频,问题启发、类比、归纳总结相结合的教学方法,让学生掌握并灵活应用错位相减法求和解决数列综合问题。
教师的教法 翻转课堂教学法.
学生的学法 自主学习微视频,积极主动探究,效果检测,合作交流展示,。
四、教具:投影仪、多媒体课件。
五、教学环节
(一)A课成果展示 ,分享收获 (二)B课课标解读,知识梳理 (三)效果检测,合作探究 (四)分组展示,小结反思
六、教学过程
教学环节 教 学 程 序 师 生 活 动 设计意图
成果展示 在自主学习任务单中选出做的好的同学的任务单展示 教师展示,学生观看。 调动学习的热情和积极性
课标分析 分析本节课的知识要点和重难点 教师分析学生识记 有目标有方向,
知识梳理 结合课件回顾学过的数列公式和结论 师问生答,教师PPT展示。 回顾知识巩固深化
学情检测 学生完成B课学习任务单(进阶练习)。 教师在学生中答疑解惑 更深入了解学情
合作探究 学生分组讨论解决任务单中的综合题,投影仪展示解答。 教师布置各组讨论任务定好讨论时间,学生小组讨论并主动展示。 培养学生的合作交流能力,分析问题并解决问题的能力,通过展示也可以进一步深化对问题的认识,并能及时地暴露问题。
进阶练习 题型一 分类讨论求前n项和1.求数列 {nxn} 的前n项和 题型二 等差、等比数列与错位相减法求和 题型三 通项与前n项和的关系以及错位相减法求和3.已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.(1)求an,bn;(2)求数列{an·bn}的前n项和Tn.挑战高考 组(1)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导。组(2)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导,并PPT展示。组(3)学生代表展示解答并讲解解题思路,同组学生补充,其他组学生点评或质疑。教师引导,并PPT展示详细求解过程。学生自主探索,合作交流。组(4)学生代表投影展示过程。大家一起规范纠错。教师规范解题步骤。 引导学生动手实践,体会不同类型的数列其不同的求和方法的解题策略。培养学生用分类讨论的数学思想来思考问题. 深化学生对错位相减法求和的认识。知识适当的综合培养观察归纳等能力。培养学生严谨的语言表达能力和方程思想。进一步巩固深化知识和方法。让学生感受到综合题其实由单个基本问题通过不同方式结合而成。关键在于探寻知识间的迁移点,化归思想是解决问题的重要途径。亲临考题最前线,激发学生斗志,调动学生学习积极性,主动性。
小结反思归纳总结 【课堂总结】这节课主要学习哪种求和方法 这种求和方法在哪些题型中体现?体会到了哪些数学思想方法?反思 教师引导学生自主完成知识、思想方法的总结。 通过反思与小结使学生对本节课的知识有一个系统全面的认识。数学思想方法是数学的灵魂,引导学生自主完成类比、化归、分类讨论、方程等思想方法的总结,从而更好的理解数学的本质。
布 置 作 业 [课后反馈]课后作业:评测练习1、数列{an}中,a1=2,an+1=an+cn(c是不为零的常数,n=1,2,3,…),且a1,a2,a3成等比数列.(1)求c的值;(2)求{an}的通项公式;(3)求数列的前n项之和Tn.2、已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.(1)求an;(2)求数列{nan}的前n项和Tn.3、已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3).(1)求数列{an}的通项公式;(2)设bn=,求数列{bn}的前n项和Tn;(3)在(2)的条件下,对任意n∈N*,Tn>都成立,求整数m的最大值. 课后完成进一步巩固,深化理解。 学生课后自主完成。 巩固本节知识,培养学生积极主动、勇于探索的精神。
七、板书设计:
1 错位相减法2.等差数列的通项公式和求和公式
3.等比数列的通项公式和求和公式4.通项与前n项和关系
八、教学反思:
