特殊平行四边形练习题二（无答案）

特殊平行四边形练习题二
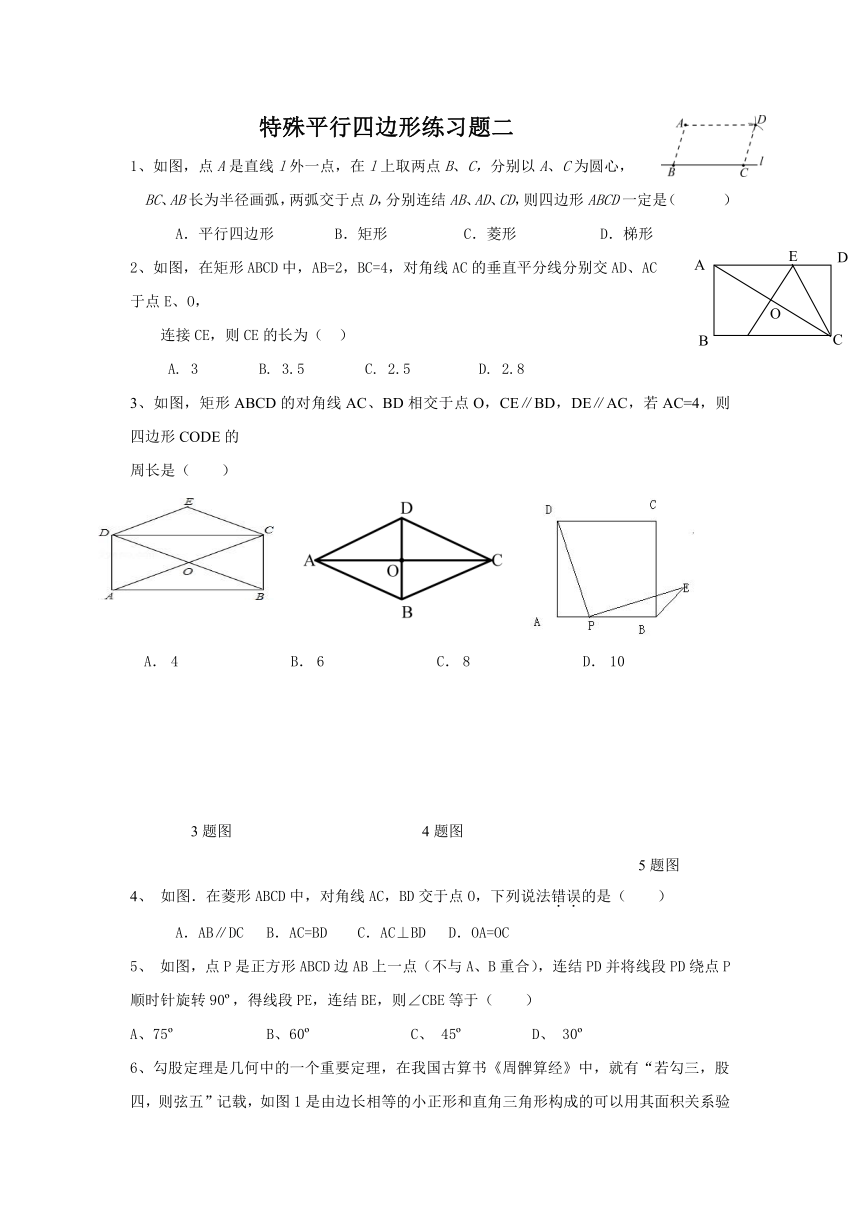
1、如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，
BC、AB长为半径画弧，两弧交于点D，分别连结AB、AD、CD，则四边形ABCD一定是（ ）
A．平行四边形 B．矩形 C．菱形 D．梯形
2、如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC
于点E、O，
连接CE，则CE的长为（ ）
A. 3 B. 3.5 C. 2.5 D. 2.8
3、如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形CODE的
周长是（　　）
　 A． 4 B． 6 C． 8 D． 10
3题图 4题图
5题图
4、 如图．在菱形ABCD中，对角线AC，BD交于点O，下列说法错误的是（ ）
A．AB∥DC B．AC=BD C．AC⊥BD D．OA=OC
5、 如图，点P是正方形ABCD边AB上一点（不与A、B重合），连结PD并将线段PD绕点P顺时针旋转90 ，得线段PE，连结BE，则∠CBE等于（ ）
A、75 B、60 C、 45 D、 30
6、勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中，就有“若勾三，股四，则弦五”记载，如图1是由边长相等的小正形和直角三角形构成的可以用其面积关系验证勾股定理。图2是由图1放入矩形内得到的，∠BAC=900,AB=3,AC=4,D,E,F,G,H,I都在矩形KLMJ的边上，则矩形KLMJ的面积为
(A)90 (B)100 (C)110 (D)121
7、如图，P是矩形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、
△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
①S1+S2=S3+S4 ② S2+S4= S1+ S3 ③若S3=2 S1，则S4=2 S2
④若S1= S2，则P点在矩形的对角线上
其中正确的结论的序号是_________________（把所有正确结论的序号都填在横线上）.
8、我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形。现有一个对角线分别为6cm和8cm的菱形，它的中点四边形的对角线长是 .
9、如图，CD与BE互相垂直平分，AD⊥DB,∠BDE=700，则∠CAD= 0.
10、如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50° ,求∠BAO的大小.
11、如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点.
（1）求证：△MBA≌△NDC；
（2）四边形MPNQ是什么样的特殊四边形？请说明理由.
12、如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE,∠A=∠D,AF=DC.
求证：四边形BCEF是平行四边形；
A
B
C
D
E
O
A
D
C
B
M
N
P
Q