沪科版七年级数学下第十章平行线和相交线复习课件
文档属性
| 名称 | 沪科版七年级数学下第十章平行线和相交线复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 42.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-03 09:59:34 | ||
图片预览




文档简介
课件21张PPT。第十章 平行线与相交线
回顾与思考学习目标:1,进一步理解和掌握邻补角,对顶角,垂线,平行线等有关定义及其性质。
2,进一步区别和掌握平行线的性质和判定,能正确利用平行线的性质和判定进行计算和证明。自学提纲:1,复习基本概念,性质,定理。
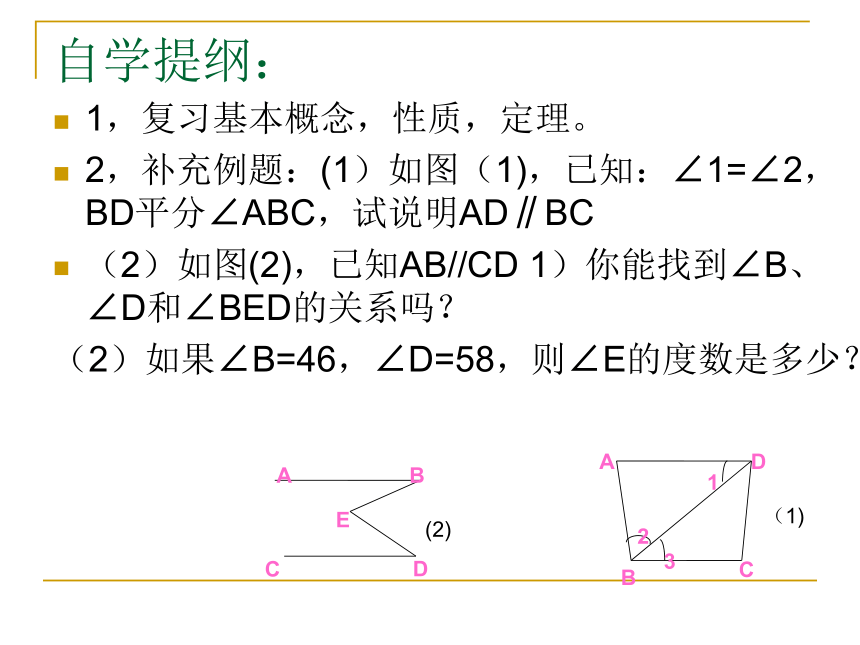
2,补充例题:(1)如图(1),已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC
(2)如图(2),已知AB//CD 1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?(1)(2)概念、性质填空:一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。二、性质:
_________的余角相等;
同角或等角的____相等;
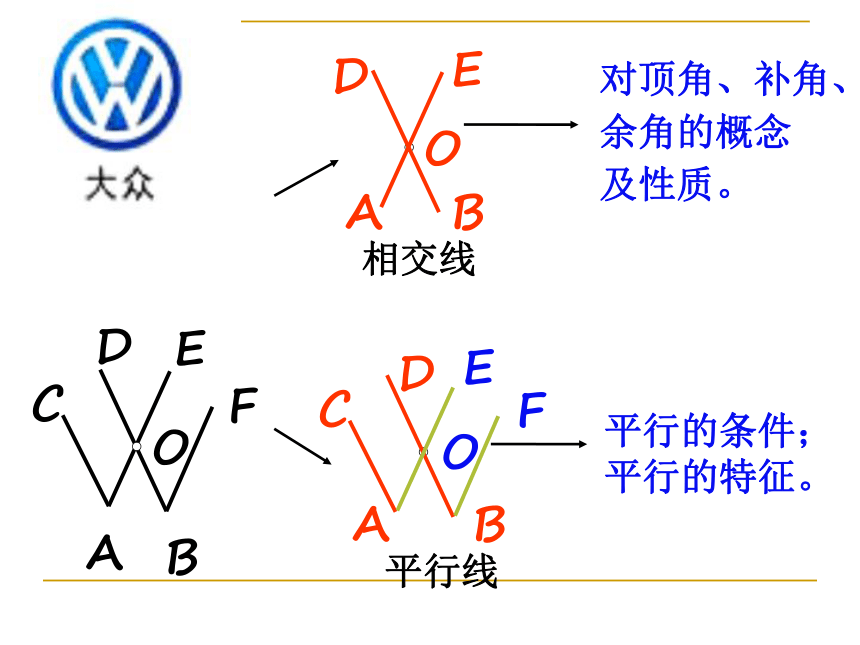
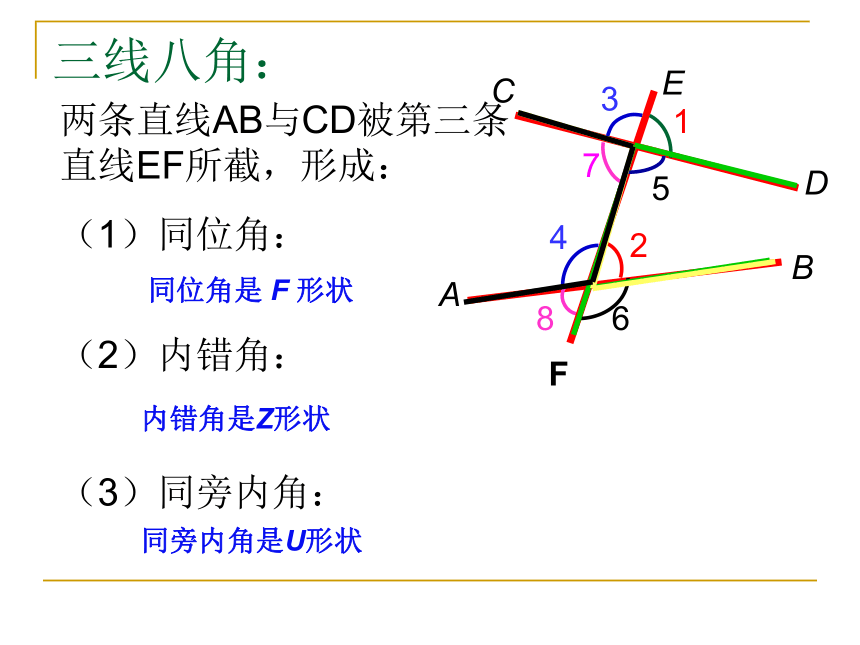
对顶角_____。直角补角对顶角同角或等角补角相等三线八角:两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
同位角是 F 形状内错角是Z形状同旁内角是U形状
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。一、平行线的判定方法:同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;二、平行线的特征:两直线平行,同位角相等;
两直线平行,内错角相等;
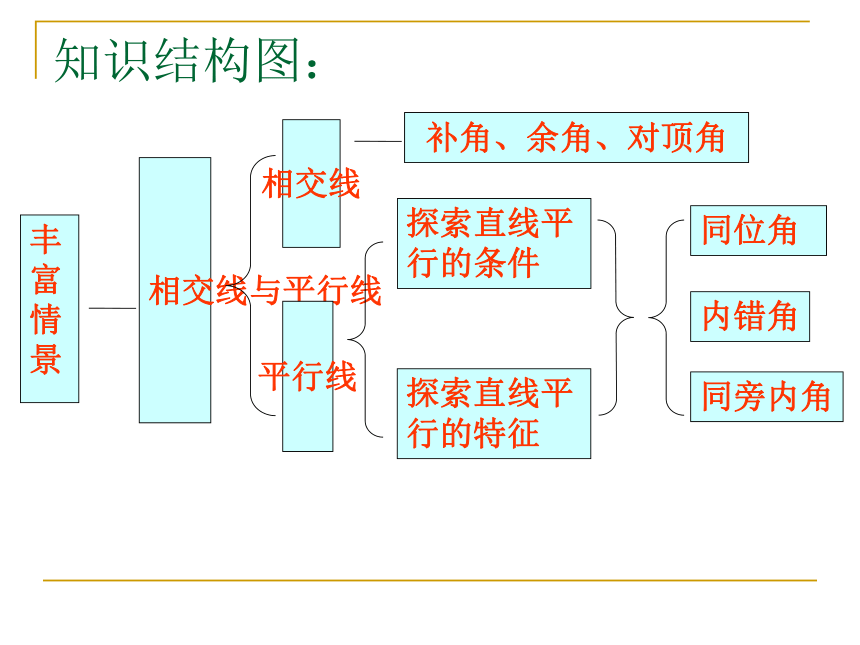
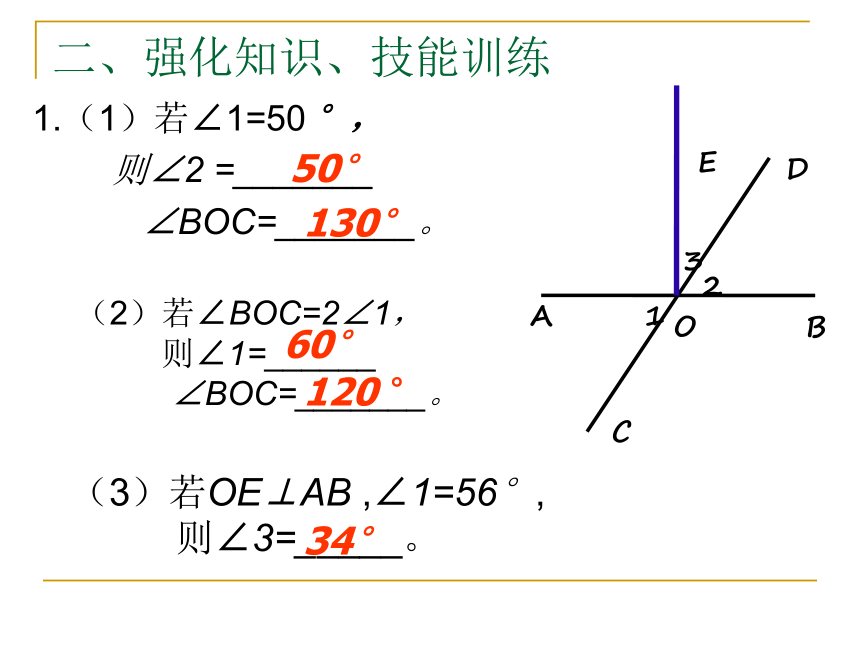
两直线平行,同旁内角互补。 知识结构图:二、强化知识、技能训练1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。 (2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。(3)若OE⊥AB ,∠1=56°,
则∠3=_____。60°120 °34°50°130°2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
=同角的余角相等2.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程) 解:∵AD∥BC ,∠A=115°, ∠D=110°
(已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
3.图中如果AC∥BD 、AE ∥BF ,那么∠A与∠B的关系如何?你是 怎样思考的?解:∵AC//BD,AE//BF(已知)
∴∠A=∠DOE
∠B=∠DOE
(两直线平行,同位角相等)
∴∠A=∠B(等量代换)4.已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180° 求证:AB//CD 证明:解一:∵∠1+∠EHB=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠EHB=∠2
(同角的补角相等)
∴AB//CD
(同位角相等,两直线平行)解二:∵∠1+∠AHG=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠AHG=∠2
(同角的补角相等)
∴AB//CD
(内错角相等,两直线平行)解三:∵∠1=∠BHG(对顶角相等)
∠1+∠2=180°(已知)
∴ ∠BHG+∠2=180°
(等量代换)
∴AB//CD
(同旁内角互补,两直线平行)证明:∵BD平分∠ABC(已知)
∴∠2=∠3(角平分线定义)
又∵∠2=∠1(已知)
∴∠3= ∠1(等量代换)
∴AD∥BC
(内错角相等,两直线平行)5.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC. 6.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
同位角相等,两直线平行两直线平行,内错角相等等量代换同位角相等,两直线平行7.如图已知AD∥BC,且DC⊥AD于D.(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)8.如图,已知AB//CD(1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?小结与思考:本节课复习了哪些内容?你有哪些收获?还存在哪些问题?课堂作业: 必做题:A组复习题,第4,7题。 选做题:B组第3题。 课外作业: 基础训练同步。谢谢!
2,进一步区别和掌握平行线的性质和判定,能正确利用平行线的性质和判定进行计算和证明。自学提纲:1,复习基本概念,性质,定理。
2,补充例题:(1)如图(1),已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC
(2)如图(2),已知AB//CD 1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?(1)(2)概念、性质填空:一、概念:
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。二、性质:
_________的余角相等;
同角或等角的____相等;
对顶角_____。直角补角对顶角同角或等角补角相等三线八角:两条直线AB与CD被第三条直线EF所截,形成:
(1)同位角:
(2)内错角:
(3)同旁内角:
同位角是 F 形状内错角是Z形状同旁内角是U形状
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。一、平行线的判定方法:同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;二、平行线的特征:两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。 知识结构图:二、强化知识、技能训练1.(1)若∠1=50 °,
则∠2 =_______
∠BOC=_______。 (2)若∠BOC=2∠1,
则∠1=______
∠BOC=_______。(3)若OE⊥AB ,∠1=56°,
则∠3=_____。60°120 °34°50°130°2. 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是_____________。
=同角的余角相等2.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(尝试用自己的方式书写说理过程) 解:∵AD∥BC ,∠A=115°, ∠D=110°
(已知)
∴∠A+ ∠B=180 °
∠D+ ∠C=180 °
(两直线平行,同旁内角互补)
∴∠B=180°﹣115°=65 °
∠C=180°-110°=70 °
3.图中如果AC∥BD 、AE ∥BF ,那么∠A与∠B的关系如何?你是 怎样思考的?解:∵AC//BD,AE//BF(已知)
∴∠A=∠DOE
∠B=∠DOE
(两直线平行,同位角相等)
∴∠A=∠B(等量代换)4.已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180° 求证:AB//CD 证明:解一:∵∠1+∠EHB=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠EHB=∠2
(同角的补角相等)
∴AB//CD
(同位角相等,两直线平行)解二:∵∠1+∠AHG=180°
(平角的定义)
∠1+∠2=180°(已知)
∴ ∠AHG=∠2
(同角的补角相等)
∴AB//CD
(内错角相等,两直线平行)解三:∵∠1=∠BHG(对顶角相等)
∠1+∠2=180°(已知)
∴ ∠BHG+∠2=180°
(等量代换)
∴AB//CD
(同旁内角互补,两直线平行)证明:∵BD平分∠ABC(已知)
∴∠2=∠3(角平分线定义)
又∵∠2=∠1(已知)
∴∠3= ∠1(等量代换)
∴AD∥BC
(内错角相等,两直线平行)5.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC. 6.如图已知∠1=∠ACB, ∠2=∠3.
求证:CD∥FH.
(小明写了相关的过程,但是却忘了写理由
请你帮他把理由补充完整)
解:∵ ∠1=∠ACB(已知)
∴DE∥BC( )
∴ ∠2 =∠DCF( )
又∵ ∠2=∠3(已知)
∴ ∠3 =∠DCF( )
∴ CD∥FH( )
同位角相等,两直线平行两直线平行,内错角相等等量代换同位角相等,两直线平行7.如图已知AD∥BC,且DC⊥AD于D.(1)DC与BC有怎样的位置关系?说说你的理由。
(2)你能说明∠1+∠2=180°吗?解:(1)∵ DC⊥AD于D(已知)
∴∠3=90°(垂直定义)
又∵ AD∥BC(已知)
∴∠3+∠DCB=180°
(两直线平行,同旁内角互补)
∴ ∠DCB=180°-90°=90°
因此 , DC⊥BC(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
又∵∠1=∠4(对顶角相等)
∴∠1+∠2=180°(等量代换)8.如图,已知AB//CD(1)你能找到∠B、∠D和∠BED的关系吗?
(2)如果∠B=46,∠D=58,则∠E的度数是多少?小结与思考:本节课复习了哪些内容?你有哪些收获?还存在哪些问题?课堂作业: 必做题:A组复习题,第4,7题。 选做题:B组第3题。 课外作业: 基础训练同步。谢谢!
