2.1直线的倾斜角与斜率 课件(共17张PPT)
文档属性
| 名称 | 2.1直线的倾斜角与斜率 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 22:32:31 | ||
图片预览




文档简介
(共17张PPT)
2.1 直线的倾斜角与斜率
【学习目标】
1、正确理解直线的倾斜角和斜率的概念;
2、掌握斜率公式的推导过程;
3、体会数形结合、分类讨论、 特殊到一般等数学思想;
【核心素养】
数学抽象、逻辑推理、数学运算。
思考:施州大桥上有若干条拉索,我们如何通过建立数学模型来描述这些拉索的不同位置?
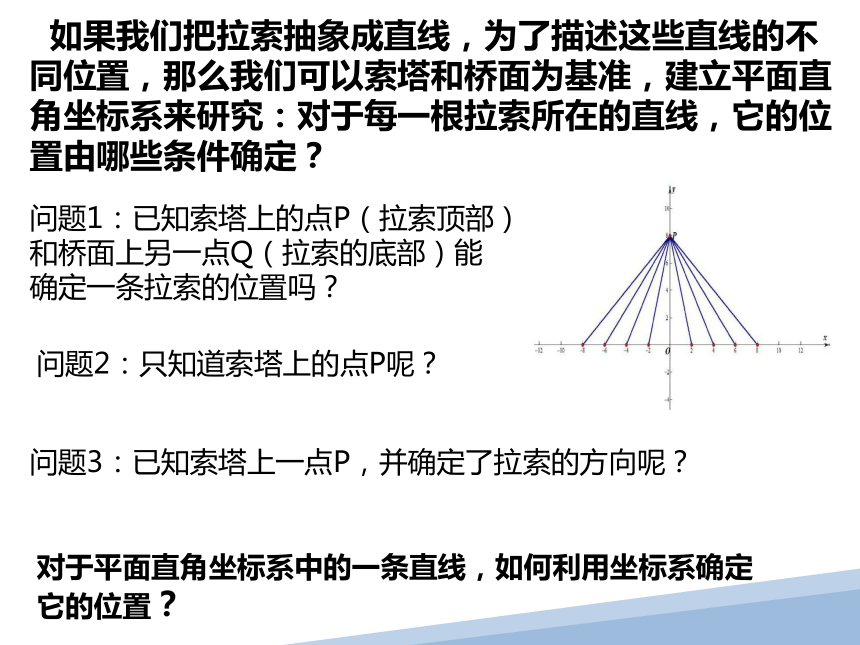
如果我们把拉索抽象成直线,为了描述这些直线的不同位置,那么我们可以索塔和桥面为基准,建立平面直角坐标系来研究:对于每一根拉索所在的直线,它的位置由哪些条件确定?
问题1:已知索塔上的点P(拉索顶部)和桥面上另一点Q(拉索的底部)能确定一条拉索的位置吗?
问题2:只知道索塔上的点P呢?
问题3:已知索塔上一点P,并确定了拉索的方向呢?
对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置?
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
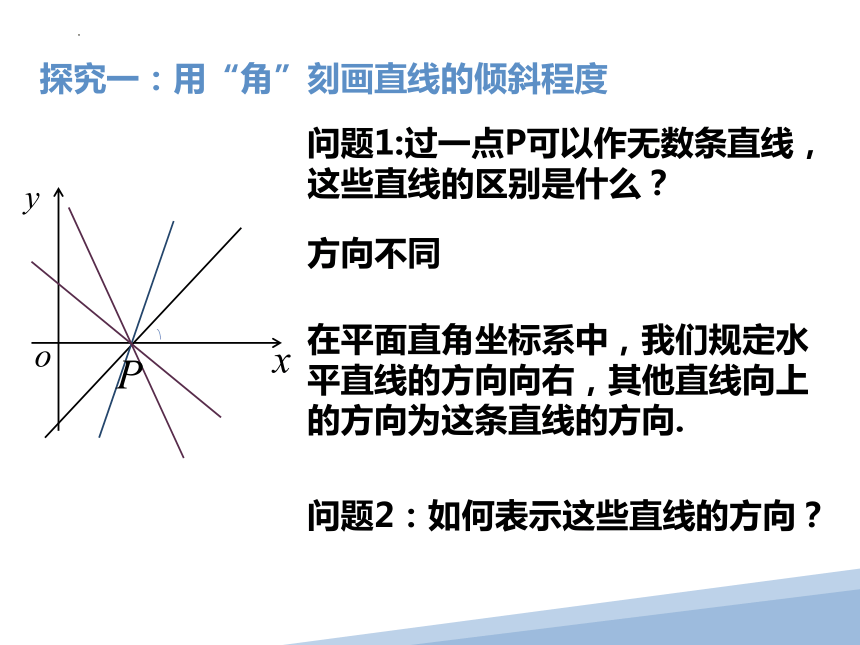
问题1:过一点P可以作无数条直线,这些直线的区别是什么?
探究一:用“角”刻画直线的倾斜程度
方向不同
问题2:如何表示这些直线的方向?
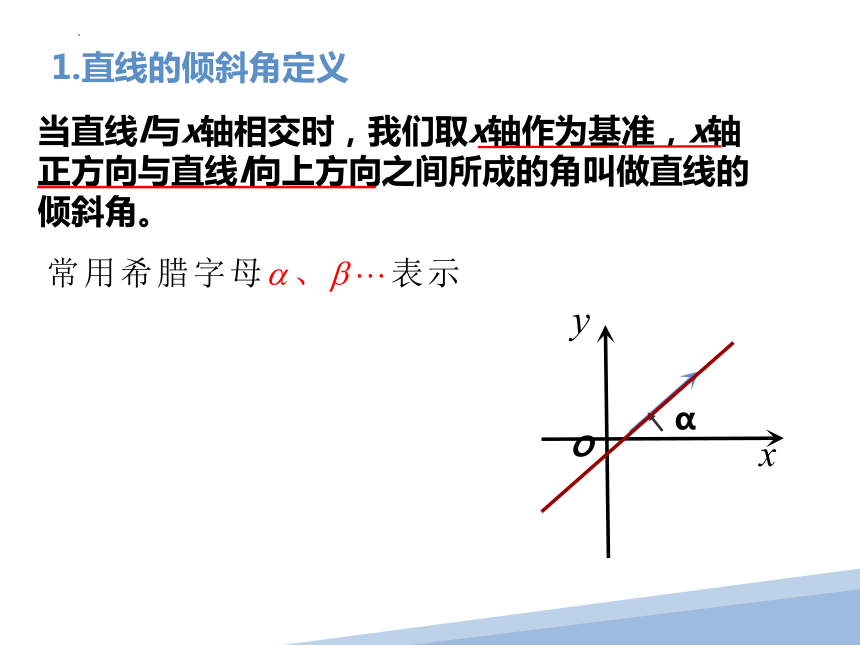
当直线l与x轴相交时,我们取x轴作为基准,x轴正方向与直线l向上方向之间所成的角叫做直线的倾斜角。
1.直线的倾斜角定义
O
α
2.倾斜角范围
我们规定直线l与x轴平行和重合时,倾斜角为0°。那么直线的倾斜角范围是?
所以:倾斜角范围:0°≤α<180°;
(3)方向不同的直线,其倾斜程度不同,倾斜角不相等.
注:(1)每一条直线都有一个确定的倾斜角;
(2)方向相同的直线,其倾斜程度相同,倾斜角相等;
在平面直角坐标系中,设直线 的倾斜角为 .
(1) 已知直线 经过 与 的坐标有什 么关系
(2)
(3)
探究二:用“斜率”刻画直线的倾斜程度
问题1:直线的倾斜角与直线上两点坐标有什么关系?
下面我们利用向量法探究上述问题.
O
α
O
O
O
O
O
k
a
O
根据正切函数图像与性质,探讨倾斜角与斜率的关系
倾斜角增大,斜率增大
倾斜角增大,斜率增大
定义:我们把一条直线的的倾斜角的正切值叫做这条直线
的斜率。斜率通常用小写字母k表示,即:
3.直线的斜率
综上所述,我们得到经过两点
的直线的斜率公式:
结论:
1、当直线与 x 轴平行或重合时,斜率为0,公式适用;
2、当直线与 x 轴垂直时,斜率不存在,公式不适用。
例1.下列说法正确的是( )
A.任一条直线都有倾斜角,所以任一条直线都有斜率;
B.直线的倾斜角越大,则直线的斜率越大:
C.两条直线倾斜角相等,则它们的斜率也相等;
D.两条直线斜率相等,则它们的倾斜角也相等;
D
典型例题
例2.
例3.如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、
BC、CA的斜率,并判断这些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角
解:
∴直线AB的倾斜角为零
当堂检测:请完成课本55页练习1-5题
谢谢聆听!
2.1 直线的倾斜角与斜率
【学习目标】
1、正确理解直线的倾斜角和斜率的概念;
2、掌握斜率公式的推导过程;
3、体会数形结合、分类讨论、 特殊到一般等数学思想;
【核心素养】
数学抽象、逻辑推理、数学运算。
思考:施州大桥上有若干条拉索,我们如何通过建立数学模型来描述这些拉索的不同位置?
如果我们把拉索抽象成直线,为了描述这些直线的不同位置,那么我们可以索塔和桥面为基准,建立平面直角坐标系来研究:对于每一根拉索所在的直线,它的位置由哪些条件确定?
问题1:已知索塔上的点P(拉索顶部)和桥面上另一点Q(拉索的底部)能确定一条拉索的位置吗?
问题2:只知道索塔上的点P呢?
问题3:已知索塔上一点P,并确定了拉索的方向呢?
对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置?
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
问题1:过一点P可以作无数条直线,这些直线的区别是什么?
探究一:用“角”刻画直线的倾斜程度
方向不同
问题2:如何表示这些直线的方向?
当直线l与x轴相交时,我们取x轴作为基准,x轴正方向与直线l向上方向之间所成的角叫做直线的倾斜角。
1.直线的倾斜角定义
O
α
2.倾斜角范围
我们规定直线l与x轴平行和重合时,倾斜角为0°。那么直线的倾斜角范围是?
所以:倾斜角范围:0°≤α<180°;
(3)方向不同的直线,其倾斜程度不同,倾斜角不相等.
注:(1)每一条直线都有一个确定的倾斜角;
(2)方向相同的直线,其倾斜程度相同,倾斜角相等;
在平面直角坐标系中,设直线 的倾斜角为 .
(1) 已知直线 经过 与 的坐标有什 么关系
(2)
(3)
探究二:用“斜率”刻画直线的倾斜程度
问题1:直线的倾斜角与直线上两点坐标有什么关系?
下面我们利用向量法探究上述问题.
O
α
O
O
O
O
O
k
a
O
根据正切函数图像与性质,探讨倾斜角与斜率的关系
倾斜角增大,斜率增大
倾斜角增大,斜率增大
定义:我们把一条直线的的倾斜角的正切值叫做这条直线
的斜率。斜率通常用小写字母k表示,即:
3.直线的斜率
综上所述,我们得到经过两点
的直线的斜率公式:
结论:
1、当直线与 x 轴平行或重合时,斜率为0,公式适用;
2、当直线与 x 轴垂直时,斜率不存在,公式不适用。
例1.下列说法正确的是( )
A.任一条直线都有倾斜角,所以任一条直线都有斜率;
B.直线的倾斜角越大,则直线的斜率越大:
C.两条直线倾斜角相等,则它们的斜率也相等;
D.两条直线斜率相等,则它们的倾斜角也相等;
D
典型例题
例2.
例3.如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、
BC、CA的斜率,并判断这些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角
解:
∴直线AB的倾斜角为零
当堂检测:请完成课本55页练习1-5题
谢谢聆听!
