3.1.3 函数的奇偶性 课件(共16张PPT)
文档属性
| 名称 | 3.1.3 函数的奇偶性 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-20 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
《函数的奇偶性》
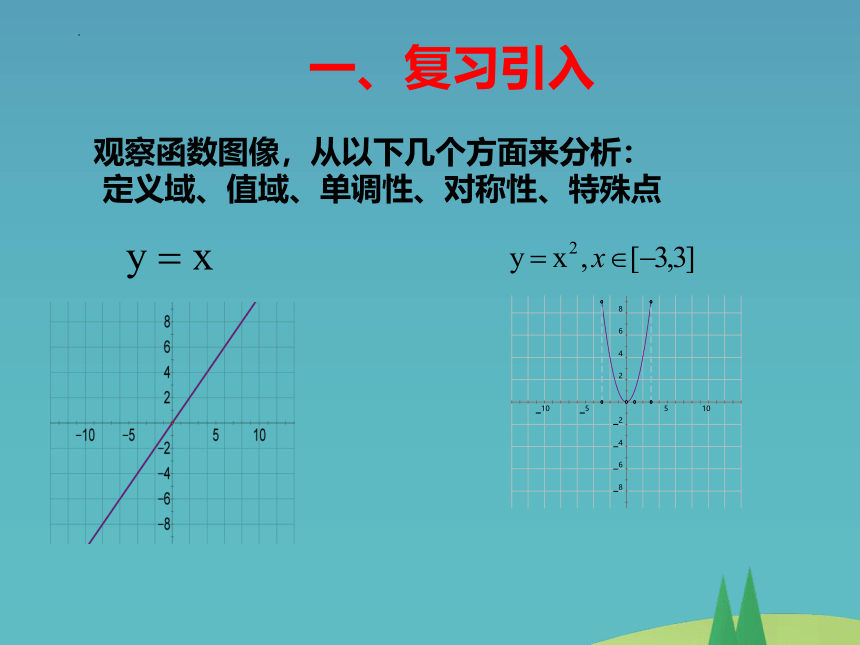
一、复习引入
观察函数图像,从以下几个方面来分析:
定义域、值域、单调性、对称性、特殊点
8
6
4
2
2
4
6
8
10
5
5
10
二、探究引导
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
g(-3)=9=g(3)
g(-2)=4=g(2)
g(-1)=1=g(1)
当自变量取相反数的时候,它们的函数值有什么关系?
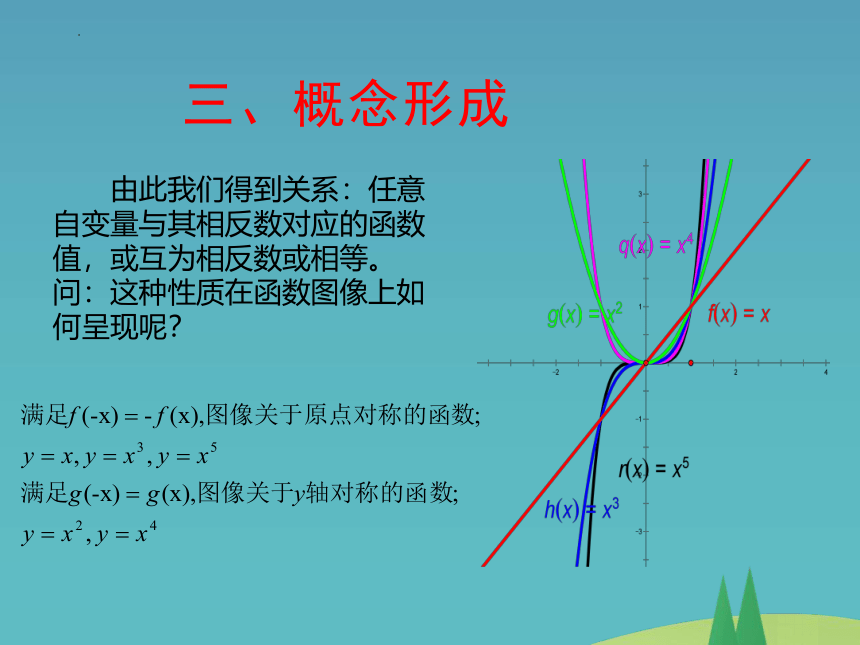
三、概念形成
由此我们得到关系:任意自变量与其相反数对应的函数值,或互为相反数或相等。
问:这种性质在函数图像上如何呈现呢?
奇函数
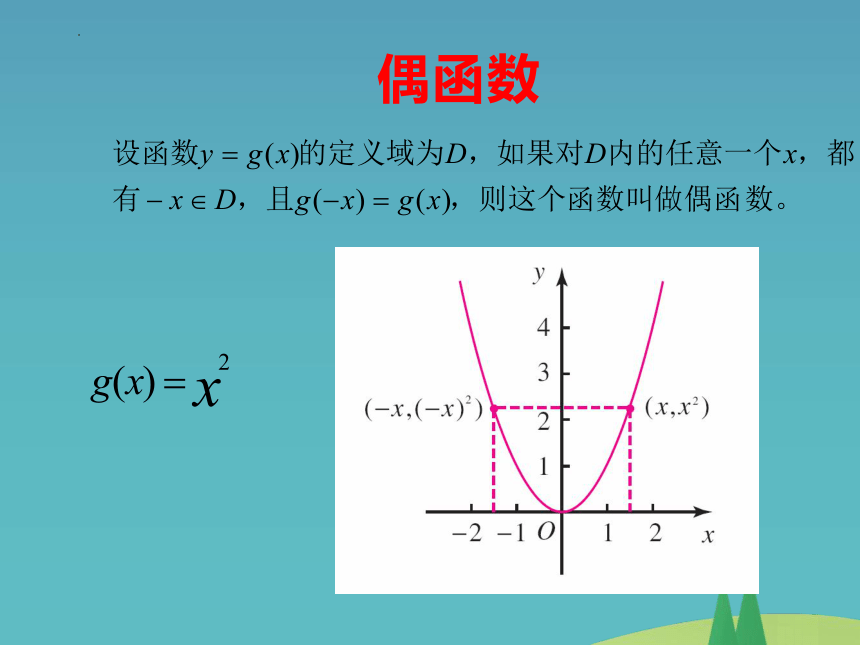
偶函数
四、概念深化
用定义判断函数奇偶性的步骤:
(1)、先求定义域,看是否关于原点对称;
若定义域不关于原点对称,则该函数一定是非奇非偶函数。
(2)、再判断f(-x)=-f(x)(或f(-x)+f(x)=0)
或f(-x)=f(x)(或f(-x)-f(x)=0)是否恒成立.
当f(x) ≠0时,还可以用f(-x)∕f(x)=±1来判断.
x
y
O
2
-2
例1 判断下列函数是否具有奇偶性
具有奇偶性的函数,其定义域有怎样的特点?
函数定义域关于原点对称.
变式练习
答案:
(1)非奇非偶函数; (2) 偶函数; (3) 偶函数;
(4)非奇非偶函数(5)既奇且偶函数
五、概念升华
观察函数f(x)=x和f(x)=1/x的图象(下图),这两个
函数图象有什么共同特征吗?
奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.
观察下面函数的图象,这两个函数图象有什么共同特征吗?
偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
f(x)=x2
f(x)=|x|
的大致图像是( )
x
y
x
y
x
y
x
y
A
B
C
D
例2 判断函数 的奇偶性。
解:函数f(x)的定义域是
∴ f(x)是奇函数
即
,关于原点对称
∵此时
∴
∵
∴
∴
课堂练习
判断下列函数的奇偶性:
本课小结
2、两个性质:
一个函数为奇函数 图象关于原点对称
一个函数为偶函数 图象关于y轴对称
谢谢大家!
《函数的奇偶性》
一、复习引入
观察函数图像,从以下几个方面来分析:
定义域、值域、单调性、对称性、特殊点
8
6
4
2
2
4
6
8
10
5
5
10
二、探究引导
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
g(-3)=9=g(3)
g(-2)=4=g(2)
g(-1)=1=g(1)
当自变量取相反数的时候,它们的函数值有什么关系?
三、概念形成
由此我们得到关系:任意自变量与其相反数对应的函数值,或互为相反数或相等。
问:这种性质在函数图像上如何呈现呢?
奇函数
偶函数
四、概念深化
用定义判断函数奇偶性的步骤:
(1)、先求定义域,看是否关于原点对称;
若定义域不关于原点对称,则该函数一定是非奇非偶函数。
(2)、再判断f(-x)=-f(x)(或f(-x)+f(x)=0)
或f(-x)=f(x)(或f(-x)-f(x)=0)是否恒成立.
当f(x) ≠0时,还可以用f(-x)∕f(x)=±1来判断.
x
y
O
2
-2
例1 判断下列函数是否具有奇偶性
具有奇偶性的函数,其定义域有怎样的特点?
函数定义域关于原点对称.
变式练习
答案:
(1)非奇非偶函数; (2) 偶函数; (3) 偶函数;
(4)非奇非偶函数(5)既奇且偶函数
五、概念升华
观察函数f(x)=x和f(x)=1/x的图象(下图),这两个
函数图象有什么共同特征吗?
奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.
观察下面函数的图象,这两个函数图象有什么共同特征吗?
偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
f(x)=x2
f(x)=|x|
的大致图像是( )
x
y
x
y
x
y
x
y
A
B
C
D
例2 判断函数 的奇偶性。
解:函数f(x)的定义域是
∴ f(x)是奇函数
即
,关于原点对称
∵此时
∴
∵
∴
∴
课堂练习
判断下列函数的奇偶性:
本课小结
2、两个性质:
一个函数为奇函数 图象关于原点对称
一个函数为偶函数 图象关于y轴对称
谢谢大家!
