2020-2021学年湖南省郴州市桂东县普乐九年一贯制学校八年级(上)期末数学试卷(含解析)
文档属性
| 名称 | 2020-2021学年湖南省郴州市桂东县普乐九年一贯制学校八年级(上)期末数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 313.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-21 10:41:18 | ||
图片预览




文档简介
2020-2021学年湖南省郴州市桂东县普乐九年一贯制学校八年级(上)期末数学试卷
一、选择题(每小题3分,本题共36分)
1.(3分)以下列各组数为边长,能构成三角形的是( )
A.1,,5 B.1,1,2 C.2,3,4 D.10,5,4
2.(3分)要使分式有意义,x应满足( )
A.x≠5 B.x≠﹣5
C.x≠5且x≠﹣5 D.x为任意实数
3.(3分)如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
4.(3分)下列各结论中,正确的是( )
A. B.
C. D.
5.(3分)已知等腰三角形的两边a、b满足=0,则此等腰三角形的周长为( )
A.7或8 B.6或10 C.6或7 D.7或10
6.(3分)计算的结果是( )
A.1 B.﹣1 C. D.
7.(3分)下列判断错误的是( )
A.代数式是分式
B.当时,分式没有意义
C.当时,分式有意义
D.当x=﹣3时,分式的值为0
8.(3分)如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
9.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.95° B.85° C.75° D.35°
10.(3分)已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
11.(3分)表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 乙方案
门号的月租费(元) 400 600
MAT手机价格(元) 15000 13000
注意事项:以上方案两年内不可变更月租费
A.500 B.516 C.517 D.600
12.(3分)对于任意的正数m,n定义运算※为m※n=计算(3※2)×(8※12)的结果为( )
A. B.20 C. D.2
二、填空题(每小题3分,本题共21分,)
13.(3分)二次根式中,a的取值范围是 .
14.(3分)若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 .
15.(3分)当a=﹣2018时,分式的值是 .
16.(3分)如图所示,DE∥BC,∠ADE=45°,∠DEB=25°,则∠ABE= 度.
17.(3分)在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2a+3b.如:1 5=﹣2×1+3×5=13.则不等式x 4<0的解集为 .
18.(3分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β= .
19.(3分)某次单词听写共20个单词,每个单词正确得10分,写错或不写扣5分,小明得分要超过90分,设他至少答对x道题,可以得不等式 .
三、解答题(本题共63分)
20.(8分)计算:
(1)(π﹣3)0﹣÷+(﹣1)﹣1;
(2)|﹣|+()﹣1﹣×.
21.(8分)解方程:
;
|x2﹣5|=4.
22.(6分)解不等式组,并把解集表示在数轴上.
23.(5分)先化简,在求值:,其中a=,b=2.
24.(8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
25.(6分)甲、乙两同学住在离学校1.8千米的A地,他们同时出发去学校,甲同学出发至100米时,发现书包忘在A地的家中,便立即返回,取了书包后立即从A地去学校,这样甲、乙二人同时到校.已知甲比乙每小时多走0.5千米,求甲、乙两人的速度.
26.(6分)如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=18°,且AD=AE,求∠EDC的度数.
27.(8分)某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
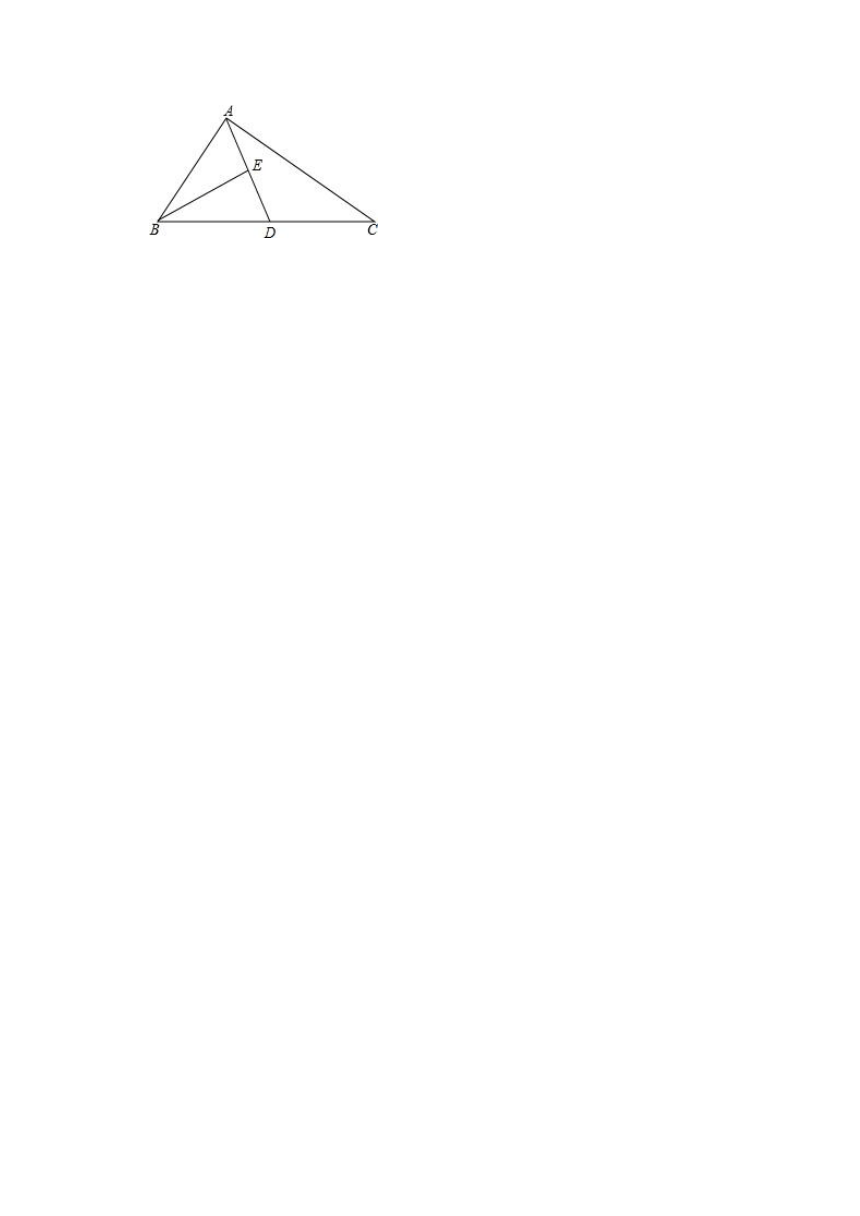
28.(8分)如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
2020-2021学年湖南省郴州市桂东县普乐九年一贯制学校八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,本题共36分)
1.(3分)以下列各组数为边长,能构成三角形的是( )
A.1,,5 B.1,1,2 C.2,3,4 D.10,5,4
【分析】根据两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
【解答】解:A、1+<5,不能组成三角形,故选项不符合题意;
B、1+1=2,不能组成三角形,故选项不符合题意;
C、2+3>4,能组成三角形,故选项符合题意;
D、4+5<10,不能组成三角形,故选项不符合题意.
故选:C.
2.(3分)要使分式有意义,x应满足( )
A.x≠5 B.x≠﹣5
C.x≠5且x≠﹣5 D.x为任意实数
【分析】分母为零,分式无意义;分母不为零,分式有意义.
【解答】解:根据分式有意义的条件,当分母x+5≠0,即x≠﹣5时,分式有意义.
∴要使分式有意义,x应满足x≠﹣5.
∴选项A、C、D错误.
故选:B.
3.(3分)如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
【分析】根据数轴上不等式解集的表示方法得出此不等式组的解集,再对各选项进行逐一判断即可.
【解答】解:由数轴上不等式解集的表示方法得出此不等式组的解集为:x≥﹣3,
A、不等式组的解集为x>﹣3,故A错误;
B、不等式组的解集为x≥﹣3,故B正确;
C、不等式组的解集为x<﹣3,故C错误;
D、不等式组的解集为﹣3<x<5,故D错误.
故选:B.
4.(3分)下列各结论中,正确的是( )
A. B.
C. D.
【分析】A、B、C、D都根据算术平方根的概念或平方根的概念逐条验算,采用排除法即可判断.
【解答】解:A、=﹣6,故选项正确;
B、=3,故选项错误;
C、=16,故选项错误;
D、,故选项错误.
故选:A.
5.(3分)已知等腰三角形的两边a、b满足=0,则此等腰三角形的周长为( )
A.7或8 B.6或10 C.6或7 D.7或10
【分析】首先根据绝对值和算术平方根均为非负数,可求出a、b的值.在等腰三角形腰和底不确定的情况下,要分类进行求解,前提等腰三角形的三边长要符合三角形的三边关系.
【解答】解:由题意,知:,解得
当a为等腰三角形的腰时,等腰三角形的三边长为2,2,3;符合三角形三边关系,
因此三角形的周长=2+2+3=7;
当b为等腰三角形的腰时,等腰三角形的三边长为3,3,2;符合三角形三边关系,
因此三角形的周长=3+3+2=8;
故选:A.
6.(3分)计算的结果是( )
A.1 B.﹣1 C. D.
【分析】几个分式相加减,根据分式加减法则进行运算,如果分式分母互为相反数,则先将其变为同分母分数,然后再直接相加减即可.
【解答】解:,故选:B.
7.(3分)下列判断错误的是( )
A.代数式是分式
B.当时,分式没有意义
C.当时,分式有意义
D.当x=﹣3时,分式的值为0
【分析】分式的分母中含有字母;分式的值为零时,分子为零,但是分母不为零.
【解答】解:A、代数式的分母中含有字母,所以该代数式是分式;故本选项判断正确;
B、当时,分式的分母为零,所以该分式没有意义;故本选项判断正确;
C、当时,分式的分子为零,分母不为零,所以该分式有意义;故本选项判断正确;
D、当x=﹣3时,分式的分母为零,该分式无意义;故本选项判断错误.
故选:D.
8.(3分)如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
【分析】根据三角形具有稳定性可得:沿对角线钉上1根木条即可.
【解答】解:根据三角形的稳定性可得他至少要再钉上1根木条,
故选:B.
9.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.95° B.85° C.75° D.35°
【分析】根据角平分线的定义求出∠ACD,根据三角形的外角的性质计算即可.
【解答】解:∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ACE=120°,
∴∠A=∠ACD﹣∠B=85°,
故选:B.
10.(3分)已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
【分析】根据不等式组的解集中共有5个整数解,求出a的范围即可.
【解答】解:∵不等式组的解集为2<x<a,共有5个整数,
∴x=3,4,5,6,7,
则a的范围为7<a≤8,
故选:A.
11.(3分)表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 乙方案
门号的月租费(元) 400 600
MAT手机价格(元) 15000 13000
注意事项:以上方案两年内不可变更月租费
A.500 B.516 C.517 D.600
【分析】由x的取值范围,结合题意找出甲、乙两种方案下两年的总花费各是多少,再由乙方案比甲方案便宜得出关于x的一元一次不等式,解不等式即可得出结论.
【解答】解:∵x为400到600之间的整数,
∴若小洁选择甲方案,需以通话费计算,若小洁选择乙方案,需以月租费计算,
甲方案使用两年总花费=24x+15000;乙方案使用两年总花费=24×600+13000=27400.
由已知得:24x+15000>27400,
解得:x>516,即x至少为517.
故选:C.
12.(3分)对于任意的正数m,n定义运算※为m※n=计算(3※2)×(8※12)的结果为( )
A. B.20 C. D.2
【分析】先利用新定义运算规定把式子(3※2)×(8※12)转化为实数运算,再按实数的混合运算求值.
【解答】解:(3※2)×(8※12)
=(﹣)×(+)
=(﹣)×(2+2)
=(﹣)×2×(+)
=2[()2﹣()2]
=2(3﹣2)
=2×1
=2.
故选:D.
二、填空题(每小题3分,本题共21分,)
13.(3分)二次根式中,a的取值范围是 a≥1 .
【分析】根据二次根式有意义的条件列出不等式,解不等式即可.
【解答】解:由题意得,a﹣1≥0,
解得,a≥1,
故答案为:a≥1.
14.(3分)若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 x<﹣3 .
【分析】先根据一元一次不等式的定义,2m+1=1且m﹣2≠0,先求出m的值是0;再把m=0代入不等式,整理得:﹣2x﹣1>5,然后利用不等式的基本性质将不等式两边同时加上1,再同时除以﹣2,不等号方向发生改变,求解即可.
【解答】解:根据不等式是一元一次不等式可得:2m+1=1且m﹣2≠0,∴m=0
∴原不等式化为:﹣2x﹣1>5
解得x<﹣3.
故答案为:x<﹣3.
15.(3分)当a=﹣2018时,分式的值是 ﹣2016 .
【分析】先将分式化简,再代入a的值即可.
【解答】解:
=
=a+2,
∵a=﹣2018,
∴原式=﹣2018+2=﹣2016,
故答案为:﹣2016.
16.(3分)如图所示,DE∥BC,∠ADE=45°,∠DEB=25°,则∠ABE= 20 度.
【分析】根据三角形的外角与内角的关系解答即可.
【解答】解:由∠ADE是三角形BDE的一个外角得∠ABE=∠ADE﹣∠DEB=45°﹣25°=20°.
故答案为:20.
17.(3分)在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2a+3b.如:1 5=﹣2×1+3×5=13.则不等式x 4<0的解集为 x>6 .
【分析】先根据所给的运算列出关于x的一元一次不等式,求出x的取值范围即可.
【解答】解:∵a b=﹣2a+3b,
∴x 4=﹣2x+3×4=﹣2x+12,
∵x 4<0,
∴﹣2x+12<0,解得x>6.
故答案为:x>6.
18.(3分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β= 240° .
【分析】本题可先根据等边三角形顶角的度数求出两底角的度数和,然后在四边形中根据四边形的内角和为360°,求出∠α+∠β的度数.
【解答】解:∵等边三角形的顶角为60°,
∴两底角和=180°﹣60°=120°;
∴∠α+∠β=360°﹣120°=240°
故答案是:240°.
19.(3分)某次单词听写共20个单词,每个单词正确得10分,写错或不写扣5分,小明得分要超过90分,设他至少答对x道题,可以得不等式 10x﹣5(20﹣x)>90 .
【分析】由小明写对x个单词,可得出小明写错或不写(20﹣x)个,利用得分=10×写对单词数量﹣5×写错或不写单词数量,结合小明得分要超过90分,即可得出关于x的一元一次不等式,此题得解.
【解答】解:∵某次单词听写共20个单词,且小明写对x个单词,
∴小明写错或不写(20﹣x)个.
根据题意得:10x﹣5(20﹣x)>90.
故答案为:10x﹣5(20﹣x)>90.
三、解答题(本题共63分)
20.(8分)计算:
(1)(π﹣3)0﹣÷+(﹣1)﹣1;
(2)|﹣|+()﹣1﹣×.
【分析】(1)先计算零次幂和负整数指数幂,再计算除法,最后算加减;
(2)先计算负整数指数幂,再算乘法化简绝对值,最后算加减.
【解答】解:(1)(π﹣3)0﹣÷+(﹣1)﹣1
=1﹣﹣1
=1﹣﹣1
=1﹣2﹣1
=﹣2;
(2)|﹣|+()﹣1﹣×
=+2﹣
=+2﹣
=2.
21.(8分)解方程:
;
|x2﹣5|=4.
【分析】(1)通过去分母、移项、合并同类项、x的系数化为1、检验解决此题.
(2)根据绝对值的定义,先去绝对值;再根据平方根的定义,求得x的值.
【解答】解:(1)由,得.
去分母,得2=2x﹣1﹣3.
移项,得2x=2+1+3.
合并同类项,得2x=6.
x的系数化为1,得x=3.
检验:当x=3时,2x﹣1≠0.
∴这个分式方程的解为x=3.
(2)∵|x2﹣5|=4,
∴x2﹣5=±4.
∴x2=9或1.
∴x=±3或±1.
22.(6分)解不等式组,并把解集表示在数轴上.
【分析】先求出每个不等式的解集,再求出不等式组的解集即可.
【解答】解:∵解不等式①得:x≥﹣1,
解不等式②得:x<0.8,
∴不等式组的解集为﹣1≤x<0.8,
在数轴上表示为:.
23.(5分)先化简,在求值:,其中a=,b=2.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将a的值代入计算即可.
【解答】解:原式=[﹣]÷
=
=a,
∵a=,
∴原式=a=.
24.(8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
【分析】(1)根据∠ACD=∠ADC,∠BCD=∠EDC=90°,可得∠ACB=∠ADE,进而运用SAS即可判定全等三角形;
(2)根据全等三角形对应角相等,运用五边形内角和,即可得到∠BAE的度数.
【解答】(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
25.(6分)甲、乙两同学住在离学校1.8千米的A地,他们同时出发去学校,甲同学出发至100米时,发现书包忘在A地的家中,便立即返回,取了书包后立即从A地去学校,这样甲、乙二人同时到校.已知甲比乙每小时多走0.5千米,求甲、乙两人的速度.
【分析】设甲的速度为x千米/时,乙的速度为(x﹣0.5)千米/时.根据两人到校所用的时间相等建立方程求出其解即可.
【解答】解:设甲的速度为x千米/时,乙的速度为(x﹣0.5)千米/时.
根据题意得:=,
解得:x=5,
经检验,x=5是原方程的根,符合题意.
所以乙的速度:5﹣0.5=4.5(千米/时).
答:甲的速度为5千米/时,乙的速度为4.5千米/时.
26.(6分)如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=18°,且AD=AE,求∠EDC的度数.
【分析】由等腰三角形的三线合一性质求得∠DAE,再根据等腰三角形的性质以及三角形内角和定理求得∠ADE,则可求得∠EDC.
【解答】解:∵AB=AC,AD⊥BC,
∴∠DAE=∠BAD=18°,
∵AD=AE,
∴∠ADE=(180°﹣∠DAE)=×(180°﹣18°)=81°,
∴∠EDC=90°﹣∠ADE=90°﹣81°=9°.
27.(8分)某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
【分析】(1)设该商店第一次购进水果x千克,则第二次购进水果2x千克,然后根据每千克的价格比第一次购进的价格贵了2元,列出方程求解即可;
(2)设每千克水果的标价是y元,然后根据两次购进水果全部售完,利润不低于950元列出不等式,然后求解即可得出答案.
【解答】解:(1)设该商店第一次购进水果x千克,则第二次购进这种水果2x千克.
由题意,得+2=,
解得x=100.
经检验,x=100是所列方程的解.
答:该商店第一次购进水果100千克.
(2)设每千克这种水果的标价是 y 元,则
(100+100×2﹣20) y+20×0.5 y≥1000+2400+950,
解得y≥15.
答:每千克这种水果的标价至少是15元.
28.(8分)如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
【分析】(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线即可得:E到BC边的距离为EF的长,然后过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
【解答】解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)过E作BC边的垂线,F为垂足,则EF为所求的E到BC边的距离,
过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴BC AG=40,即×10 AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF=AG=×8=4.
∴E到BC边的距离为4.
一、选择题(每小题3分,本题共36分)
1.(3分)以下列各组数为边长,能构成三角形的是( )
A.1,,5 B.1,1,2 C.2,3,4 D.10,5,4
2.(3分)要使分式有意义,x应满足( )
A.x≠5 B.x≠﹣5
C.x≠5且x≠﹣5 D.x为任意实数
3.(3分)如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
4.(3分)下列各结论中,正确的是( )
A. B.
C. D.
5.(3分)已知等腰三角形的两边a、b满足=0,则此等腰三角形的周长为( )
A.7或8 B.6或10 C.6或7 D.7或10
6.(3分)计算的结果是( )
A.1 B.﹣1 C. D.
7.(3分)下列判断错误的是( )
A.代数式是分式
B.当时,分式没有意义
C.当时,分式有意义
D.当x=﹣3时,分式的值为0
8.(3分)如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
9.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.95° B.85° C.75° D.35°
10.(3分)已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
11.(3分)表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 乙方案
门号的月租费(元) 400 600
MAT手机价格(元) 15000 13000
注意事项:以上方案两年内不可变更月租费
A.500 B.516 C.517 D.600
12.(3分)对于任意的正数m,n定义运算※为m※n=计算(3※2)×(8※12)的结果为( )
A. B.20 C. D.2
二、填空题(每小题3分,本题共21分,)
13.(3分)二次根式中,a的取值范围是 .
14.(3分)若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 .
15.(3分)当a=﹣2018时,分式的值是 .
16.(3分)如图所示,DE∥BC,∠ADE=45°,∠DEB=25°,则∠ABE= 度.
17.(3分)在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2a+3b.如:1 5=﹣2×1+3×5=13.则不等式x 4<0的解集为 .
18.(3分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β= .
19.(3分)某次单词听写共20个单词,每个单词正确得10分,写错或不写扣5分,小明得分要超过90分,设他至少答对x道题,可以得不等式 .
三、解答题(本题共63分)
20.(8分)计算:
(1)(π﹣3)0﹣÷+(﹣1)﹣1;
(2)|﹣|+()﹣1﹣×.
21.(8分)解方程:
;
|x2﹣5|=4.
22.(6分)解不等式组,并把解集表示在数轴上.
23.(5分)先化简,在求值:,其中a=,b=2.
24.(8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
25.(6分)甲、乙两同学住在离学校1.8千米的A地,他们同时出发去学校,甲同学出发至100米时,发现书包忘在A地的家中,便立即返回,取了书包后立即从A地去学校,这样甲、乙二人同时到校.已知甲比乙每小时多走0.5千米,求甲、乙两人的速度.
26.(6分)如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=18°,且AD=AE,求∠EDC的度数.
27.(8分)某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
28.(8分)如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
2020-2021学年湖南省郴州市桂东县普乐九年一贯制学校八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,本题共36分)
1.(3分)以下列各组数为边长,能构成三角形的是( )
A.1,,5 B.1,1,2 C.2,3,4 D.10,5,4
【分析】根据两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
【解答】解:A、1+<5,不能组成三角形,故选项不符合题意;
B、1+1=2,不能组成三角形,故选项不符合题意;
C、2+3>4,能组成三角形,故选项符合题意;
D、4+5<10,不能组成三角形,故选项不符合题意.
故选:C.
2.(3分)要使分式有意义,x应满足( )
A.x≠5 B.x≠﹣5
C.x≠5且x≠﹣5 D.x为任意实数
【分析】分母为零,分式无意义;分母不为零,分式有意义.
【解答】解:根据分式有意义的条件,当分母x+5≠0,即x≠﹣5时,分式有意义.
∴要使分式有意义,x应满足x≠﹣5.
∴选项A、C、D错误.
故选:B.
3.(3分)如图,数轴上表示的是下列哪个不等式组的解集( )
A. B. C. D.
【分析】根据数轴上不等式解集的表示方法得出此不等式组的解集,再对各选项进行逐一判断即可.
【解答】解:由数轴上不等式解集的表示方法得出此不等式组的解集为:x≥﹣3,
A、不等式组的解集为x>﹣3,故A错误;
B、不等式组的解集为x≥﹣3,故B正确;
C、不等式组的解集为x<﹣3,故C错误;
D、不等式组的解集为﹣3<x<5,故D错误.
故选:B.
4.(3分)下列各结论中,正确的是( )
A. B.
C. D.
【分析】A、B、C、D都根据算术平方根的概念或平方根的概念逐条验算,采用排除法即可判断.
【解答】解:A、=﹣6,故选项正确;
B、=3,故选项错误;
C、=16,故选项错误;
D、,故选项错误.
故选:A.
5.(3分)已知等腰三角形的两边a、b满足=0,则此等腰三角形的周长为( )
A.7或8 B.6或10 C.6或7 D.7或10
【分析】首先根据绝对值和算术平方根均为非负数,可求出a、b的值.在等腰三角形腰和底不确定的情况下,要分类进行求解,前提等腰三角形的三边长要符合三角形的三边关系.
【解答】解:由题意,知:,解得
当a为等腰三角形的腰时,等腰三角形的三边长为2,2,3;符合三角形三边关系,
因此三角形的周长=2+2+3=7;
当b为等腰三角形的腰时,等腰三角形的三边长为3,3,2;符合三角形三边关系,
因此三角形的周长=3+3+2=8;
故选:A.
6.(3分)计算的结果是( )
A.1 B.﹣1 C. D.
【分析】几个分式相加减,根据分式加减法则进行运算,如果分式分母互为相反数,则先将其变为同分母分数,然后再直接相加减即可.
【解答】解:,故选:B.
7.(3分)下列判断错误的是( )
A.代数式是分式
B.当时,分式没有意义
C.当时,分式有意义
D.当x=﹣3时,分式的值为0
【分析】分式的分母中含有字母;分式的值为零时,分子为零,但是分母不为零.
【解答】解:A、代数式的分母中含有字母,所以该代数式是分式;故本选项判断正确;
B、当时,分式的分母为零,所以该分式没有意义;故本选项判断正确;
C、当时,分式的分子为零,分母不为零,所以该分式有意义;故本选项判断正确;
D、当x=﹣3时,分式的分母为零,该分式无意义;故本选项判断错误.
故选:D.
8.(3分)如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少要再钉上木条的根数是( )
A.0 B.1 C.2 D.3
【分析】根据三角形具有稳定性可得:沿对角线钉上1根木条即可.
【解答】解:根据三角形的稳定性可得他至少要再钉上1根木条,
故选:B.
9.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.95° B.85° C.75° D.35°
【分析】根据角平分线的定义求出∠ACD,根据三角形的外角的性质计算即可.
【解答】解:∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ACE=120°,
∴∠A=∠ACD﹣∠B=85°,
故选:B.
10.(3分)已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
【分析】根据不等式组的解集中共有5个整数解,求出a的范围即可.
【解答】解:∵不等式组的解集为2<x<a,共有5个整数,
∴x=3,4,5,6,7,
则a的范围为7<a≤8,
故选:A.
11.(3分)表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 乙方案
门号的月租费(元) 400 600
MAT手机价格(元) 15000 13000
注意事项:以上方案两年内不可变更月租费
A.500 B.516 C.517 D.600
【分析】由x的取值范围,结合题意找出甲、乙两种方案下两年的总花费各是多少,再由乙方案比甲方案便宜得出关于x的一元一次不等式,解不等式即可得出结论.
【解答】解:∵x为400到600之间的整数,
∴若小洁选择甲方案,需以通话费计算,若小洁选择乙方案,需以月租费计算,
甲方案使用两年总花费=24x+15000;乙方案使用两年总花费=24×600+13000=27400.
由已知得:24x+15000>27400,
解得:x>516,即x至少为517.
故选:C.
12.(3分)对于任意的正数m,n定义运算※为m※n=计算(3※2)×(8※12)的结果为( )
A. B.20 C. D.2
【分析】先利用新定义运算规定把式子(3※2)×(8※12)转化为实数运算,再按实数的混合运算求值.
【解答】解:(3※2)×(8※12)
=(﹣)×(+)
=(﹣)×(2+2)
=(﹣)×2×(+)
=2[()2﹣()2]
=2(3﹣2)
=2×1
=2.
故选:D.
二、填空题(每小题3分,本题共21分,)
13.(3分)二次根式中,a的取值范围是 a≥1 .
【分析】根据二次根式有意义的条件列出不等式,解不等式即可.
【解答】解:由题意得,a﹣1≥0,
解得,a≥1,
故答案为:a≥1.
14.(3分)若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 x<﹣3 .
【分析】先根据一元一次不等式的定义,2m+1=1且m﹣2≠0,先求出m的值是0;再把m=0代入不等式,整理得:﹣2x﹣1>5,然后利用不等式的基本性质将不等式两边同时加上1,再同时除以﹣2,不等号方向发生改变,求解即可.
【解答】解:根据不等式是一元一次不等式可得:2m+1=1且m﹣2≠0,∴m=0
∴原不等式化为:﹣2x﹣1>5
解得x<﹣3.
故答案为:x<﹣3.
15.(3分)当a=﹣2018时,分式的值是 ﹣2016 .
【分析】先将分式化简,再代入a的值即可.
【解答】解:
=
=a+2,
∵a=﹣2018,
∴原式=﹣2018+2=﹣2016,
故答案为:﹣2016.
16.(3分)如图所示,DE∥BC,∠ADE=45°,∠DEB=25°,则∠ABE= 20 度.
【分析】根据三角形的外角与内角的关系解答即可.
【解答】解:由∠ADE是三角形BDE的一个外角得∠ABE=∠ADE﹣∠DEB=45°﹣25°=20°.
故答案为:20.
17.(3分)在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2a+3b.如:1 5=﹣2×1+3×5=13.则不等式x 4<0的解集为 x>6 .
【分析】先根据所给的运算列出关于x的一元一次不等式,求出x的取值范围即可.
【解答】解:∵a b=﹣2a+3b,
∴x 4=﹣2x+3×4=﹣2x+12,
∵x 4<0,
∴﹣2x+12<0,解得x>6.
故答案为:x>6.
18.(3分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β= 240° .
【分析】本题可先根据等边三角形顶角的度数求出两底角的度数和,然后在四边形中根据四边形的内角和为360°,求出∠α+∠β的度数.
【解答】解:∵等边三角形的顶角为60°,
∴两底角和=180°﹣60°=120°;
∴∠α+∠β=360°﹣120°=240°
故答案是:240°.
19.(3分)某次单词听写共20个单词,每个单词正确得10分,写错或不写扣5分,小明得分要超过90分,设他至少答对x道题,可以得不等式 10x﹣5(20﹣x)>90 .
【分析】由小明写对x个单词,可得出小明写错或不写(20﹣x)个,利用得分=10×写对单词数量﹣5×写错或不写单词数量,结合小明得分要超过90分,即可得出关于x的一元一次不等式,此题得解.
【解答】解:∵某次单词听写共20个单词,且小明写对x个单词,
∴小明写错或不写(20﹣x)个.
根据题意得:10x﹣5(20﹣x)>90.
故答案为:10x﹣5(20﹣x)>90.
三、解答题(本题共63分)
20.(8分)计算:
(1)(π﹣3)0﹣÷+(﹣1)﹣1;
(2)|﹣|+()﹣1﹣×.
【分析】(1)先计算零次幂和负整数指数幂,再计算除法,最后算加减;
(2)先计算负整数指数幂,再算乘法化简绝对值,最后算加减.
【解答】解:(1)(π﹣3)0﹣÷+(﹣1)﹣1
=1﹣﹣1
=1﹣﹣1
=1﹣2﹣1
=﹣2;
(2)|﹣|+()﹣1﹣×
=+2﹣
=+2﹣
=2.
21.(8分)解方程:
;
|x2﹣5|=4.
【分析】(1)通过去分母、移项、合并同类项、x的系数化为1、检验解决此题.
(2)根据绝对值的定义,先去绝对值;再根据平方根的定义,求得x的值.
【解答】解:(1)由,得.
去分母,得2=2x﹣1﹣3.
移项,得2x=2+1+3.
合并同类项,得2x=6.
x的系数化为1,得x=3.
检验:当x=3时,2x﹣1≠0.
∴这个分式方程的解为x=3.
(2)∵|x2﹣5|=4,
∴x2﹣5=±4.
∴x2=9或1.
∴x=±3或±1.
22.(6分)解不等式组,并把解集表示在数轴上.
【分析】先求出每个不等式的解集,再求出不等式组的解集即可.
【解答】解:∵解不等式①得:x≥﹣1,
解不等式②得:x<0.8,
∴不等式组的解集为﹣1≤x<0.8,
在数轴上表示为:.
23.(5分)先化简,在求值:,其中a=,b=2.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将a的值代入计算即可.
【解答】解:原式=[﹣]÷
=
=a,
∵a=,
∴原式=a=.
24.(8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
【分析】(1)根据∠ACD=∠ADC,∠BCD=∠EDC=90°,可得∠ACB=∠ADE,进而运用SAS即可判定全等三角形;
(2)根据全等三角形对应角相等,运用五边形内角和,即可得到∠BAE的度数.
【解答】(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
25.(6分)甲、乙两同学住在离学校1.8千米的A地,他们同时出发去学校,甲同学出发至100米时,发现书包忘在A地的家中,便立即返回,取了书包后立即从A地去学校,这样甲、乙二人同时到校.已知甲比乙每小时多走0.5千米,求甲、乙两人的速度.
【分析】设甲的速度为x千米/时,乙的速度为(x﹣0.5)千米/时.根据两人到校所用的时间相等建立方程求出其解即可.
【解答】解:设甲的速度为x千米/时,乙的速度为(x﹣0.5)千米/时.
根据题意得:=,
解得:x=5,
经检验,x=5是原方程的根,符合题意.
所以乙的速度:5﹣0.5=4.5(千米/时).
答:甲的速度为5千米/时,乙的速度为4.5千米/时.
26.(6分)如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=18°,且AD=AE,求∠EDC的度数.
【分析】由等腰三角形的三线合一性质求得∠DAE,再根据等腰三角形的性质以及三角形内角和定理求得∠ADE,则可求得∠EDC.
【解答】解:∵AB=AC,AD⊥BC,
∴∠DAE=∠BAD=18°,
∵AD=AE,
∴∠ADE=(180°﹣∠DAE)=×(180°﹣18°)=81°,
∴∠EDC=90°﹣∠ADE=90°﹣81°=9°.
27.(8分)某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
【分析】(1)设该商店第一次购进水果x千克,则第二次购进水果2x千克,然后根据每千克的价格比第一次购进的价格贵了2元,列出方程求解即可;
(2)设每千克水果的标价是y元,然后根据两次购进水果全部售完,利润不低于950元列出不等式,然后求解即可得出答案.
【解答】解:(1)设该商店第一次购进水果x千克,则第二次购进这种水果2x千克.
由题意,得+2=,
解得x=100.
经检验,x=100是所列方程的解.
答:该商店第一次购进水果100千克.
(2)设每千克这种水果的标价是 y 元,则
(100+100×2﹣20) y+20×0.5 y≥1000+2400+950,
解得y≥15.
答:每千克这种水果的标价至少是15元.
28.(8分)如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
【分析】(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线即可得:E到BC边的距离为EF的长,然后过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
【解答】解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)过E作BC边的垂线,F为垂足,则EF为所求的E到BC边的距离,
过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴BC AG=40,即×10 AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF=AG=×8=4.
∴E到BC边的距离为4.
同课章节目录
