6.2.3一元一次方程的应用 课件(共24张PPT)
文档属性
| 名称 | 6.2.3一元一次方程的应用 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 984.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-22 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.2.3一元一次方程的应用
华师大版 七年级 下册
教学目标
教学目标:1.掌握用一元一次方程解决实际问题的方法.
2.经历应用方程解决实际问题的过程,发展分析问题,解决
问题的能力,进一步体会方程模型的作用.
教学重点:用一元一次方程解决实际问题的一般步骤.
教学难点:找出实际问题中的等量关系,并根据等量关系列出方程.
新知导入
情境引入
小明用45元钱买了面值为2元和3元的邮票共20张,问他买了多少张面值为2元的邮票
分析:若设他买了x张面值为2元的邮票,则面值为3元的邮票为20-x张,
2元的一共用去2x元,3元的一共用去3(20-x)元
因为一共用去45元,所以可列方程
2x+3(20-x)=45
新知讲解
合作学习
例6 如图,天平的两个盘内分别盛有51g和45g的盐,问应从盘A中拿出多少盐放到盘B中,才能使两者所盛盐的质量相等
A 51g
B 45g
x g
A (51-x)g
B (45+x)g
分析 从盘A中拿出一些盐放到盘B中,使两盘所盛盐的质量相等,于是有这样的等量关系:
盘A现有盐的质量=盘B现有盐的质量.
用方程解决问题的关键
是弄清题意,找出等量关系.
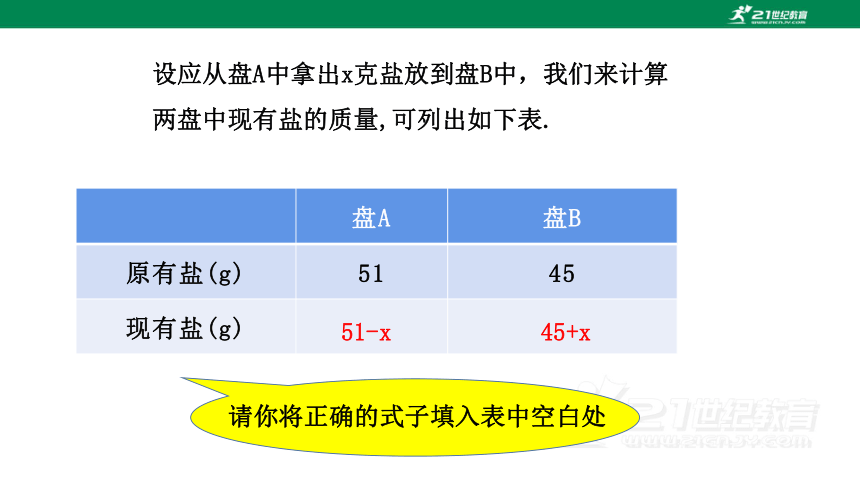
设应从盘A中拿出x克盐放到盘B中,我们来计算
两盘中现有盐的质量,可列出如下表.
盘A 盘B
原有盐(g) 51 45
现有盐(g)
请你将正确的式子填入表中空白处
51-x
45+x
解:设应从盘A中拿出x g盐放到盘B中,则根据题意,得
51-x=45+x.
解这个方程,得
x=3.
经检验,符合题意.
答:应从盘A中拿出3g盐放到盘B中.
提炼概念
解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数,
列,列一元一次方程
解,解方程
验,检验答案是否符合题意
答,解答
典例精讲
例7:学校团委组织65名新团员为学校建花坛搬砖.女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块.问这些新团员中有多少名男同学
读题,找找看,题目告诉了
我们哪些等量关系
分析 题目告诉了我们好几个等量关系,其中有这
样的等量关系:
男同学搬砖数+女同学搬砖数=搬砖总数.
分析
新团员中有x名男同学,列表如下
男同学 女同学 总数
参加人数(个) x 65
每人搬砖数(块) 8×4 6×4
共搬砖数(块) 1800
解:设新团员中有x名男同学,根据题意,得
32x+24(65-x)=1800.
解这个方程,得
x=30.
经检验,符合题意.
答:这些新团员中有30名男同学.
归纳概念
这一过程也可以简单地表述为:
概括
抽象
检验
问题
方程
解答
分析
求解
其中分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数(设元) ;
(2)找出问题所给出的等量关系,它反映了未知量与已知量之间的关系;
(3)对这个等量关系中涉及的量,列出所需的代数
式,根据等量关系,列出方程.
在设未知数和作出解答时,应注意量的单位.
课堂练习
1.一条山路,小明从山下往山顶走3小时还有1千米才到山顶,若从山顶走到山下只用150分钟,已知下山速度是上山速度的1.5倍,求山下到山顶的路程.设上山速度为x千米/分钟,则所列方程为( ).
D
2.某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
解:设前年这个学校购买了x台计算机,
根据题意得: x+2x+4x=140,
解得: x=20.
答:前年这个学校购买了20台计算机.
3.学校田径队的小刚在400米跑测试中,先以6m/s的速度,平均速度跑了大部分路程,最后8m/s的速度冲刺到达终点,成绩1分零5秒.问小刚在冲刺阶段花了多少时间?
分析
小刚在冲刺阶段花了y秒
6m/s 8m/s 总计
所花 时间
路程
y
65-y
400
65
解 设:小刚在冲刺阶段花了y秒
6(65-y)+8y=400
解得 y=5
答:小刚在冲刺阶段花了5秒
4.课外活动中一些学生分组参加活动,原来每组8人,后来重新编组.每组12人,这样比原来减少2组,问这些学生共有多少人?
分析
这些学生共有x人.
解 设这些学生共有x人.
解得 x=48
答:这些学生共有48人.
5.自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车,某出租车公司拟在今明两年共投资6000万元改造220辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改造费用是30万元,预计明年每辆无人驾驶出租车的改造费用可下降40%.求明年改造的无人驾驶出租车的数量.
解:设明年改造无人驾驶出租车x辆,则今年改造无人驾驶出租车(220-x)辆.
根据题意,
得30(220-x)+30x(1-40%)x=6000,
解得x=50.
答:明年改造的无人驾驶出租车有50辆.
课堂总结
归纳
用方程解决实际问题的过程
问题
方程
过程
分析
抽象
求解
检验
其中分析和抽象的过程通常包括:
1.弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
2.找出问题所给的等量关系,它反映了未知量与已知量之间的关系;
3.对这个等量关系中涉及的量,列出所需的代数式,根据等量关系,列出方程.
在设未知数和做出解答时,应注意量的单位.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.2.3一元一次方程的应用
华师大版 七年级 下册
教学目标
教学目标:1.掌握用一元一次方程解决实际问题的方法.
2.经历应用方程解决实际问题的过程,发展分析问题,解决
问题的能力,进一步体会方程模型的作用.
教学重点:用一元一次方程解决实际问题的一般步骤.
教学难点:找出实际问题中的等量关系,并根据等量关系列出方程.
新知导入
情境引入
小明用45元钱买了面值为2元和3元的邮票共20张,问他买了多少张面值为2元的邮票
分析:若设他买了x张面值为2元的邮票,则面值为3元的邮票为20-x张,
2元的一共用去2x元,3元的一共用去3(20-x)元
因为一共用去45元,所以可列方程
2x+3(20-x)=45
新知讲解
合作学习
例6 如图,天平的两个盘内分别盛有51g和45g的盐,问应从盘A中拿出多少盐放到盘B中,才能使两者所盛盐的质量相等
A 51g
B 45g
x g
A (51-x)g
B (45+x)g
分析 从盘A中拿出一些盐放到盘B中,使两盘所盛盐的质量相等,于是有这样的等量关系:
盘A现有盐的质量=盘B现有盐的质量.
用方程解决问题的关键
是弄清题意,找出等量关系.
设应从盘A中拿出x克盐放到盘B中,我们来计算
两盘中现有盐的质量,可列出如下表.
盘A 盘B
原有盐(g) 51 45
现有盐(g)
请你将正确的式子填入表中空白处
51-x
45+x
解:设应从盘A中拿出x g盐放到盘B中,则根据题意,得
51-x=45+x.
解这个方程,得
x=3.
经检验,符合题意.
答:应从盘A中拿出3g盐放到盘B中.
提炼概念
解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数,
列,列一元一次方程
解,解方程
验,检验答案是否符合题意
答,解答
典例精讲
例7:学校团委组织65名新团员为学校建花坛搬砖.女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块.问这些新团员中有多少名男同学
读题,找找看,题目告诉了
我们哪些等量关系
分析 题目告诉了我们好几个等量关系,其中有这
样的等量关系:
男同学搬砖数+女同学搬砖数=搬砖总数.
分析
新团员中有x名男同学,列表如下
男同学 女同学 总数
参加人数(个) x 65
每人搬砖数(块) 8×4 6×4
共搬砖数(块) 1800
解:设新团员中有x名男同学,根据题意,得
32x+24(65-x)=1800.
解这个方程,得
x=30.
经检验,符合题意.
答:这些新团员中有30名男同学.
归纳概念
这一过程也可以简单地表述为:
概括
抽象
检验
问题
方程
解答
分析
求解
其中分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数(设元) ;
(2)找出问题所给出的等量关系,它反映了未知量与已知量之间的关系;
(3)对这个等量关系中涉及的量,列出所需的代数
式,根据等量关系,列出方程.
在设未知数和作出解答时,应注意量的单位.
课堂练习
1.一条山路,小明从山下往山顶走3小时还有1千米才到山顶,若从山顶走到山下只用150分钟,已知下山速度是上山速度的1.5倍,求山下到山顶的路程.设上山速度为x千米/分钟,则所列方程为( ).
D
2.某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
解:设前年这个学校购买了x台计算机,
根据题意得: x+2x+4x=140,
解得: x=20.
答:前年这个学校购买了20台计算机.
3.学校田径队的小刚在400米跑测试中,先以6m/s的速度,平均速度跑了大部分路程,最后8m/s的速度冲刺到达终点,成绩1分零5秒.问小刚在冲刺阶段花了多少时间?
分析
小刚在冲刺阶段花了y秒
6m/s 8m/s 总计
所花 时间
路程
y
65-y
400
65
解 设:小刚在冲刺阶段花了y秒
6(65-y)+8y=400
解得 y=5
答:小刚在冲刺阶段花了5秒
4.课外活动中一些学生分组参加活动,原来每组8人,后来重新编组.每组12人,这样比原来减少2组,问这些学生共有多少人?
分析
这些学生共有x人.
解 设这些学生共有x人.
解得 x=48
答:这些学生共有48人.
5.自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车,某出租车公司拟在今明两年共投资6000万元改造220辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改造费用是30万元,预计明年每辆无人驾驶出租车的改造费用可下降40%.求明年改造的无人驾驶出租车的数量.
解:设明年改造无人驾驶出租车x辆,则今年改造无人驾驶出租车(220-x)辆.
根据题意,
得30(220-x)+30x(1-40%)x=6000,
解得x=50.
答:明年改造的无人驾驶出租车有50辆.
课堂总结
归纳
用方程解决实际问题的过程
问题
方程
过程
分析
抽象
求解
检验
其中分析和抽象的过程通常包括:
1.弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
2.找出问题所给的等量关系,它反映了未知量与已知量之间的关系;
3.对这个等量关系中涉及的量,列出所需的代数式,根据等量关系,列出方程.
在设未知数和做出解答时,应注意量的单位.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
