6.3.1 实践与探索 等积变形问题课件(共26张PPT)
文档属性
| 名称 | 6.3.1 实践与探索 等积变形问题课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-29 15:47:14 | ||
图片预览








文档简介
(共26张PPT)
6.3.1 实践与探索--等积变形问题
华师大版 七年级 下册
教学目标
教学目标:1.通过分析图形问题中的基本等量关系,建立方程解决问题.
2.进一步了解一元一次方程在解决实际问题中的应用.
教学重点:能利用一元一次方程解决简单的图形问题.
教学难点:借助立体及平面图形学会分析复杂问题中的数量关系和等量关系,建立一元一次方程,使实际问题数学化.
新知导入
情境引入
一个关于数学的童话故事
很久很久以前,有一个国王,他有一个非常漂亮的女儿,一年年,漂亮的公主长大了.为了给自己的女儿找到一个好的归宿,国王准备在全国范围内为自己的女儿招亲,因为这是一个农业大国,这个国家的人民非常勤劳。所以,国王要为自己女儿找到一个全国最勤劳最聪明的驸马.
亲爱的子民们:
如果你是20-25岁的年轻小伙子,你拥有勤劳的双手和智慧的头脑,你就有权来参加招亲.
参加招亲的年轻人都将得到一个长60米的栅栏,如果你用这个栅栏围成的长方形耕地种得了所有人中最多的粮食,那么你会成为驸马!
怎样才能围成最大的长方形呢?
新知讲解
合作学习
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
(1)如果长方形的宽是长的,求这个长方形的长和宽;
用一根长60厘米的铁丝围成一个长方形,
(3)若设长方形的面积为x平方厘米,能否直接列方程?
(1)解:设长为x,则宽为,
由题意得:2(x+)=60
解得:x=18
则
所以长为18厘米,宽为12厘米.
(2)解:设长为x,则宽为x-4,
由题意得:2(x+x-4)=60
解得:x=17
则x-4=17-4=13
面积=17×13=221(平方厘米)
所以长方形的面积是221平方厘米.
(3)设长方形的面积为x平方厘米,不能找出等量关系, 不能直接列出方程.
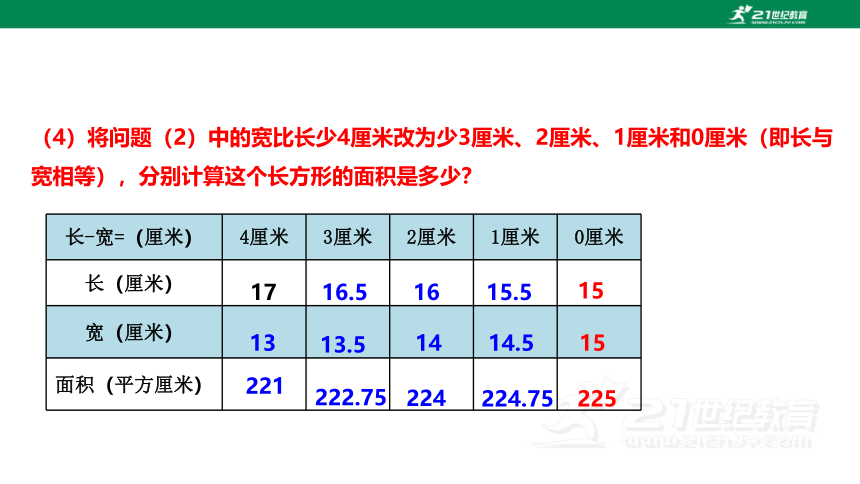
(4)将问题(2)中的宽比长少4厘米改为少3厘米、2厘米、1厘米和0厘米(即长与宽相等),分别计算这个长方形的面积是多少?
长-宽=(厘米) 4厘米 3厘米 2厘米 1厘米 0厘米
长(厘米)
宽(厘米)
面积(平方厘米)
17
13
16.5
13.5
16
14
15.5
14.5
15
15
221
222.75
224
224.75
225
提炼概念
注意:长-宽=?也就是长比宽多多少或者宽比长少多少.
观察以上数据,你能发现长方形的面积和长方形的长、宽之差有什么关系么?
长方形在周长一定的条件下,它的长与宽越接近,面积就越大;当长与宽相等,即成为正方形时,面积最大.
实际上,如果两个正数的和不变,当这两个数相等时,它们的积最大,通过以后的学习,我们就会知道其中的道理.
若 ,则
招亲启事
亲爱的子民们:
如果你是20-25岁的年轻小伙子,你拥有勤劳的双手和智慧的头脑,你就有权来参加招亲。
参加招亲的年轻人都将得到一个长60米的栅栏,如果你用这个栅栏围成的长方形耕地,并种得了所有人中最多的粮食,那么你会成为驸马!
现在有谁能回答国王提出的问题呢?
解:当长方形的长为15厘米,宽为15厘米时
长方形的面积最大,最大值=
实际上,若把这根铁丝围成任何封闭的平面图形(包括随意七凹八凸的不规则图形),面积最大的是圆。这里面的道理需要较为高深的数学知识,在以后的学习中,我们继续去探究其中的道理.
续接故事:如果没有要求围成方形地,那么,围成什么样形状的地,面积最大?
典例精讲
例: 如图,小明家打算靠墙(墙长14米)修建一个长方形的养鸡场,另三边用35米长的竹篱笆围成,小明的爸爸打算让鸡场的长比宽多2米,小明的妈妈打算让鸡场的长比宽多5米,你认为他们谁的设计合理 按照这种设计,鸡场的面积是多少平方米
解:设鸡场的宽为x米.
①若按小明爸爸的设计,则其长应为(x+2)米.
x+2+2x=35
x=11.
因为11+2=13(米)<墙长14米,
所以小明爸爸的设计合理,
这时鸡场的面积为13x11=143(平方米).
经检验:符合题意
②若按小明妈妈的设计,则其长应为(x+5)米.
x+5+2x=35
x=10.
因为10+5=15(米)>墙长14米,
所以小明妈妈的设计不合理.
经检验:不符合题意
归纳概念
提醒:运用一元一次方程解决实际问题时,要注意解的合理性,即所得结果必须符合实际情况,所以方程的解需要进行检验.
课堂练习
1.一个长方形的周长是40 cm,若将长减少8 cm,宽增加2 cm,长方形就变成了正方形,则正方形的边长为( )
A.6 cm B.7 cm C.8 cm D. 9 cm
B
2.根据图中给出的信息,可得正确的方程是( )
A
A. B.
C. D.
3. 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
解:设圆的半径为r m,则正方形的边长为
[r+2(π-2)]m.根据题意,得
答:铁丝的长为8π m,圆的面积较大.
因为4π×4>4π×π,所以16π>4π2,
所以圆的面积大.
正方形的面积为 [4+2(π-2)]2=4π2(m 2).
所以圆的面积是 π×42=16π(m 2),
所以铁丝的长为2πr=8π(m).
2πr=4(r+2π-4),解得 r=4.
4. 一种牙膏出口处直径为5 mm,小明每次刷牙都挤出1 cm长的牙膏,这样一支牙膏可以用36次,该品牌牙膏推出新包装,只是将出口处直径改为6 mm,小明还是按习惯每次挤出1 cm的牙膏,这样,这一支牙膏能用多少次?
5.周长为80厘米的铁丝,围成一个长方形.
(1)当长方形的长和宽为多少厘米时,面积最大?最大面积是多少?
(2)利用上面探究的结果,尝试下题:
若a>0,b>0且a+b=3,求ab的最大值.
6.某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的前提下,水箱的高度将由原先的4 m变为多少米?
解:设水箱的高变为x m:
π×22×4
π×1.62×x
=
解得 x=5
因此,水箱的高度变成了5 m.
课堂总结
应用一元一次方程
图形等长变化
应用一元一次方程解决实际问题的步骤
图形等积变化
列
⑤检
④解
设
审
⑥答
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.3.1 实践与探索--等积变形问题
华师大版 七年级 下册
教学目标
教学目标:1.通过分析图形问题中的基本等量关系,建立方程解决问题.
2.进一步了解一元一次方程在解决实际问题中的应用.
教学重点:能利用一元一次方程解决简单的图形问题.
教学难点:借助立体及平面图形学会分析复杂问题中的数量关系和等量关系,建立一元一次方程,使实际问题数学化.
新知导入
情境引入
一个关于数学的童话故事
很久很久以前,有一个国王,他有一个非常漂亮的女儿,一年年,漂亮的公主长大了.为了给自己的女儿找到一个好的归宿,国王准备在全国范围内为自己的女儿招亲,因为这是一个农业大国,这个国家的人民非常勤劳。所以,国王要为自己女儿找到一个全国最勤劳最聪明的驸马.
亲爱的子民们:
如果你是20-25岁的年轻小伙子,你拥有勤劳的双手和智慧的头脑,你就有权来参加招亲.
参加招亲的年轻人都将得到一个长60米的栅栏,如果你用这个栅栏围成的长方形耕地种得了所有人中最多的粮食,那么你会成为驸马!
怎样才能围成最大的长方形呢?
新知讲解
合作学习
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
(1)如果长方形的宽是长的,求这个长方形的长和宽;
用一根长60厘米的铁丝围成一个长方形,
(3)若设长方形的面积为x平方厘米,能否直接列方程?
(1)解:设长为x,则宽为,
由题意得:2(x+)=60
解得:x=18
则
所以长为18厘米,宽为12厘米.
(2)解:设长为x,则宽为x-4,
由题意得:2(x+x-4)=60
解得:x=17
则x-4=17-4=13
面积=17×13=221(平方厘米)
所以长方形的面积是221平方厘米.
(3)设长方形的面积为x平方厘米,不能找出等量关系, 不能直接列出方程.
(4)将问题(2)中的宽比长少4厘米改为少3厘米、2厘米、1厘米和0厘米(即长与宽相等),分别计算这个长方形的面积是多少?
长-宽=(厘米) 4厘米 3厘米 2厘米 1厘米 0厘米
长(厘米)
宽(厘米)
面积(平方厘米)
17
13
16.5
13.5
16
14
15.5
14.5
15
15
221
222.75
224
224.75
225
提炼概念
注意:长-宽=?也就是长比宽多多少或者宽比长少多少.
观察以上数据,你能发现长方形的面积和长方形的长、宽之差有什么关系么?
长方形在周长一定的条件下,它的长与宽越接近,面积就越大;当长与宽相等,即成为正方形时,面积最大.
实际上,如果两个正数的和不变,当这两个数相等时,它们的积最大,通过以后的学习,我们就会知道其中的道理.
若 ,则
招亲启事
亲爱的子民们:
如果你是20-25岁的年轻小伙子,你拥有勤劳的双手和智慧的头脑,你就有权来参加招亲。
参加招亲的年轻人都将得到一个长60米的栅栏,如果你用这个栅栏围成的长方形耕地,并种得了所有人中最多的粮食,那么你会成为驸马!
现在有谁能回答国王提出的问题呢?
解:当长方形的长为15厘米,宽为15厘米时
长方形的面积最大,最大值=
实际上,若把这根铁丝围成任何封闭的平面图形(包括随意七凹八凸的不规则图形),面积最大的是圆。这里面的道理需要较为高深的数学知识,在以后的学习中,我们继续去探究其中的道理.
续接故事:如果没有要求围成方形地,那么,围成什么样形状的地,面积最大?
典例精讲
例: 如图,小明家打算靠墙(墙长14米)修建一个长方形的养鸡场,另三边用35米长的竹篱笆围成,小明的爸爸打算让鸡场的长比宽多2米,小明的妈妈打算让鸡场的长比宽多5米,你认为他们谁的设计合理 按照这种设计,鸡场的面积是多少平方米
解:设鸡场的宽为x米.
①若按小明爸爸的设计,则其长应为(x+2)米.
x+2+2x=35
x=11.
因为11+2=13(米)<墙长14米,
所以小明爸爸的设计合理,
这时鸡场的面积为13x11=143(平方米).
经检验:符合题意
②若按小明妈妈的设计,则其长应为(x+5)米.
x+5+2x=35
x=10.
因为10+5=15(米)>墙长14米,
所以小明妈妈的设计不合理.
经检验:不符合题意
归纳概念
提醒:运用一元一次方程解决实际问题时,要注意解的合理性,即所得结果必须符合实际情况,所以方程的解需要进行检验.
课堂练习
1.一个长方形的周长是40 cm,若将长减少8 cm,宽增加2 cm,长方形就变成了正方形,则正方形的边长为( )
A.6 cm B.7 cm C.8 cm D. 9 cm
B
2.根据图中给出的信息,可得正确的方程是( )
A
A. B.
C. D.
3. 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
解:设圆的半径为r m,则正方形的边长为
[r+2(π-2)]m.根据题意,得
答:铁丝的长为8π m,圆的面积较大.
因为4π×4>4π×π,所以16π>4π2,
所以圆的面积大.
正方形的面积为 [4+2(π-2)]2=4π2(m 2).
所以圆的面积是 π×42=16π(m 2),
所以铁丝的长为2πr=8π(m).
2πr=4(r+2π-4),解得 r=4.
4. 一种牙膏出口处直径为5 mm,小明每次刷牙都挤出1 cm长的牙膏,这样一支牙膏可以用36次,该品牌牙膏推出新包装,只是将出口处直径改为6 mm,小明还是按习惯每次挤出1 cm的牙膏,这样,这一支牙膏能用多少次?
5.周长为80厘米的铁丝,围成一个长方形.
(1)当长方形的长和宽为多少厘米时,面积最大?最大面积是多少?
(2)利用上面探究的结果,尝试下题:
若a>0,b>0且a+b=3,求ab的最大值.
6.某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的前提下,水箱的高度将由原先的4 m变为多少米?
解:设水箱的高变为x m:
π×22×4
π×1.62×x
=
解得 x=5
因此,水箱的高度变成了5 m.
课堂总结
应用一元一次方程
图形等长变化
应用一元一次方程解决实际问题的步骤
图形等积变化
列
⑤检
④解
设
审
⑥答
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
