湖南省益阳市桃江县三校协作体2022-2023学年八年级上学期线上期末测试 数学试题 (含答案)
文档属性
| 名称 | 湖南省益阳市桃江县三校协作体2022-2023学年八年级上学期线上期末测试 数学试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-23 15:53:00 | ||
图片预览

文档简介
2022桃江县三校协作体线上期末测试
八年级数学
一、选择题(共12题,共48分)
如果一个数的立方根是这个数本身,那么这个数是
A. B. C. D. 或
把二次根式 化简为
A. B. C. D.
在式子 ,,,, 中,属于分式的有
A. 个 B. 个 C. 个 D. 个
下列各式中,正确的是
A. B.
C. D.
下列命题中的真命题是
A.相等的角是对顶角
B.内错角相等
C.如果 ,那么
D.两个角的两边分别平行,则这两个角相等
某个体户用 元购进单价相同的毛巾一批,留下 条自己用,而将其余的毛巾每条加价 元出售,售完后盈利 元,问他购进这批毛巾共几条?如果设这批毛巾共有 条,下面所列方程正确的有
A.
B.
C.
D.
下列各组数中,能作为一个三角形三边边长的是
A. ,, B. ,, C. ,, D. ,,
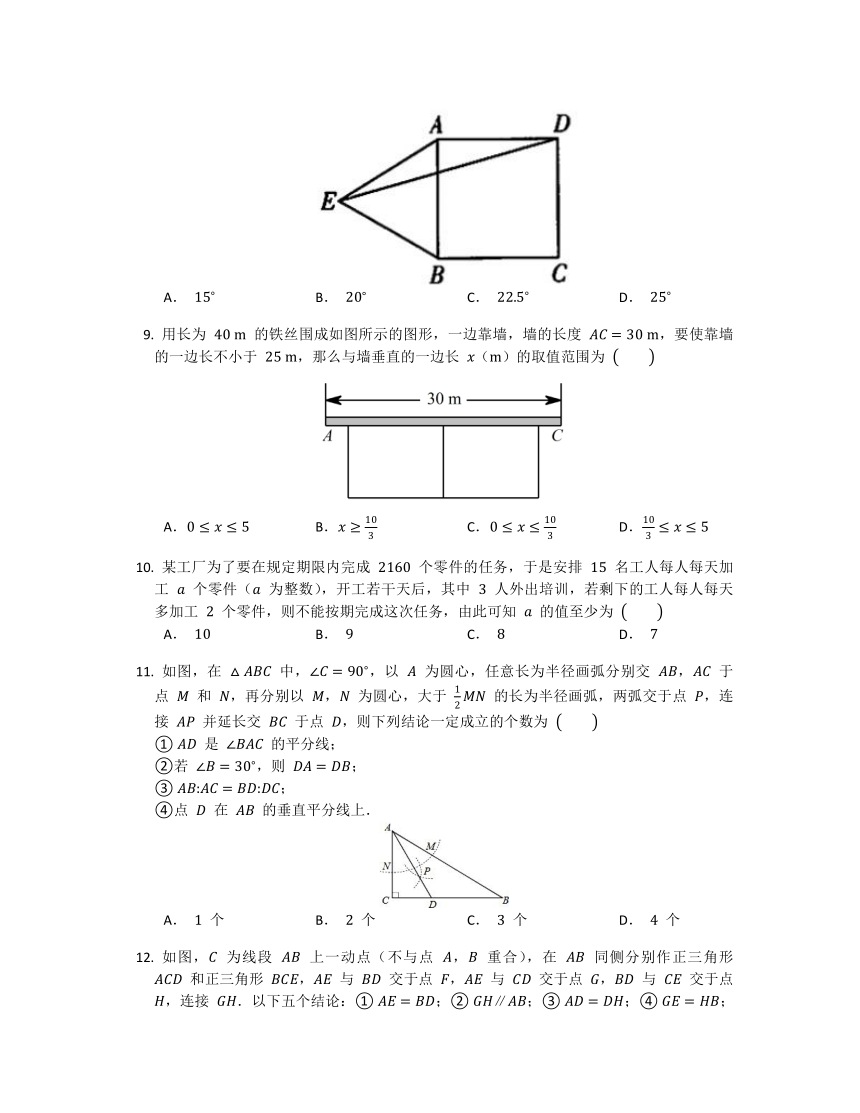
如图,以正方形 的边 为一边向外作等边三角形 ,则 的度数为
A. B. C. D.
用长为 的铁丝围成如图所示的图形,一边靠墙,墙的长度 ,要使靠墙的一边长不小于 ,那么与墙垂直的一边长 ()的取值范围为
A. B. C. D.
某工厂为了要在规定期限内完成 个零件的任务,于是安排 名工人每人每天加工 个零件( 为整数),开工若干天后,其中 人外出培训,若剩下的工人每人每天多加工 个零件,则不能按期完成这次任务,由此可知 的值至少为
A. B. C. D.
如图,在 中,,以 为圆心,任意长为半径画弧分别交 , 于点 和 ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,则下列结论一定成立的个数为
① 是 的平分线;
②若 ,则 ;
③ ;
④点 在 的垂直平分线上.
A. 个 B. 个 C. 个 D. 个
如图, 为线段 上一动点(不与点 , 重合),在 同侧分别作正三角形 和正三角形 , 与 交于点 , 与 交于点 , 与 交于点 ,连接 .以下五个结论:① ;② ;③ ;④ ;⑤ ,一定成立的是
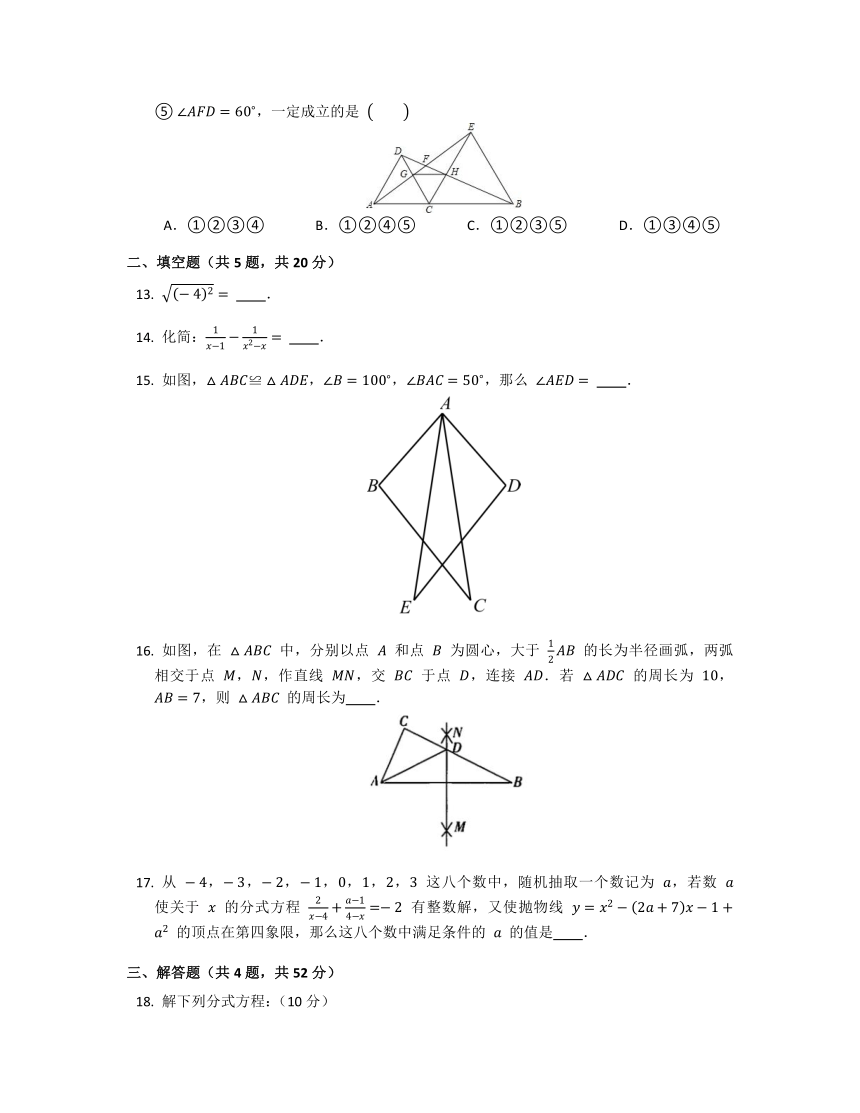
A.①②③④ B.①②④⑤ C.①②③⑤ D.①③④⑤
二、填空题(共5题,共20分)
.
化简: .
如图,,,,那么 .
如图,在 中,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 ,,作直线 ,交 于点 ,连接 .若 的周长为 ,,则 的周长为 .
从 ,,,,,,, 这八个数中,随机抽取一个数记为 ,若数 使关于 的分式方程 有整数解,又使抛物线 的顶点在第四象限,那么这八个数中满足条件的 的值是 .
三、解答题(共4题,共52分)
解下列分式方程:(10分)
(1) .
(2) .
某公司购买了一批 , 型芯片,其中 型芯片的单价比 型芯片的单价少 元,已知该公司用 元购买 型芯片的条数与用 元购买 型芯片的条数相等.(12分)
(1) 求该公司购买的 , 型芯片的单价各是多少元?
(2) 若两种芯片共购买了 条,且购买的总费用为 元,求购买了多少条 型芯片?
问题:在 中,,, 为 的平分线,探究 ,, 之间的数量关系.请你完成下列探究过程:(14分)
(1) 观察图形,猜想 ,, 之间的数量关系为 .
(2) 在对(1)中的猜想进行证明时,当推出 后,可进一步推出 度.
(3) 为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在 上截取 ,连接 ,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.
在平面直角坐标系中,已知点 ,,连接 .(16分)
(1) 如图①, 在 轴负半轴上,且 交 于点 、交 于点 ,求证:.
(2) 如图②,在()的条件下,连接 ,求证:.
(3) 如图③, 为 的中点, 是 轴上一个动点,连接 ,作 交 轴于 ,猜想 ,, 三条线段之间的数量关系,并说明理由.
答案
1-12 DADDC BCADB CB
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
17. 【答案】 ,
18. 【答案】
(1) 去分母得:解得:经检验 是增根,分式方程无解.
(2) 去分母得:去括号得:移项合并得:解得:经检验 是分式方程的解.
19. 【答案】
(1) 设 型芯片的单价为 元/条,则 型芯片的单价为 元/条,
根据题意得:解得:经检验, 是原方程的解,且符合题意.
.
答: 型芯片的单价为 元/条, 型芯片的单价为 元/条.
(2) 设购买 条 型芯片,则购买 条 型芯片,
根据题意得:解得:答:购买了 条 型芯片.
20. 【答案】
(1)
(2)
(3) 画出图形如图,在 上截取 ,连接 .
,,
,
.
,
,
.
,,
,,
.
,,
,
,
,
,
.
21. 【答案】
(1) ,,
,
,,
,
,
在 和 中,
.
(2) 如图,过点 作 ,,
,,
,
在 和 中,
,
,
,,,
平分 ,
.
(3) .
如图,连 ,
,,
,
,,
,
,
在 和 中,
,
,
.
八年级数学
一、选择题(共12题,共48分)
如果一个数的立方根是这个数本身,那么这个数是
A. B. C. D. 或
把二次根式 化简为
A. B. C. D.
在式子 ,,,, 中,属于分式的有
A. 个 B. 个 C. 个 D. 个
下列各式中,正确的是
A. B.
C. D.
下列命题中的真命题是
A.相等的角是对顶角
B.内错角相等
C.如果 ,那么
D.两个角的两边分别平行,则这两个角相等
某个体户用 元购进单价相同的毛巾一批,留下 条自己用,而将其余的毛巾每条加价 元出售,售完后盈利 元,问他购进这批毛巾共几条?如果设这批毛巾共有 条,下面所列方程正确的有
A.
B.
C.
D.
下列各组数中,能作为一个三角形三边边长的是
A. ,, B. ,, C. ,, D. ,,
如图,以正方形 的边 为一边向外作等边三角形 ,则 的度数为
A. B. C. D.
用长为 的铁丝围成如图所示的图形,一边靠墙,墙的长度 ,要使靠墙的一边长不小于 ,那么与墙垂直的一边长 ()的取值范围为
A. B. C. D.
某工厂为了要在规定期限内完成 个零件的任务,于是安排 名工人每人每天加工 个零件( 为整数),开工若干天后,其中 人外出培训,若剩下的工人每人每天多加工 个零件,则不能按期完成这次任务,由此可知 的值至少为
A. B. C. D.
如图,在 中,,以 为圆心,任意长为半径画弧分别交 , 于点 和 ,再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,则下列结论一定成立的个数为
① 是 的平分线;
②若 ,则 ;
③ ;
④点 在 的垂直平分线上.
A. 个 B. 个 C. 个 D. 个
如图, 为线段 上一动点(不与点 , 重合),在 同侧分别作正三角形 和正三角形 , 与 交于点 , 与 交于点 , 与 交于点 ,连接 .以下五个结论:① ;② ;③ ;④ ;⑤ ,一定成立的是
A.①②③④ B.①②④⑤ C.①②③⑤ D.①③④⑤
二、填空题(共5题,共20分)
.
化简: .
如图,,,,那么 .
如图,在 中,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 ,,作直线 ,交 于点 ,连接 .若 的周长为 ,,则 的周长为 .
从 ,,,,,,, 这八个数中,随机抽取一个数记为 ,若数 使关于 的分式方程 有整数解,又使抛物线 的顶点在第四象限,那么这八个数中满足条件的 的值是 .
三、解答题(共4题,共52分)
解下列分式方程:(10分)
(1) .
(2) .
某公司购买了一批 , 型芯片,其中 型芯片的单价比 型芯片的单价少 元,已知该公司用 元购买 型芯片的条数与用 元购买 型芯片的条数相等.(12分)
(1) 求该公司购买的 , 型芯片的单价各是多少元?
(2) 若两种芯片共购买了 条,且购买的总费用为 元,求购买了多少条 型芯片?
问题:在 中,,, 为 的平分线,探究 ,, 之间的数量关系.请你完成下列探究过程:(14分)
(1) 观察图形,猜想 ,, 之间的数量关系为 .
(2) 在对(1)中的猜想进行证明时,当推出 后,可进一步推出 度.
(3) 为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在 上截取 ,连接 ,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.
在平面直角坐标系中,已知点 ,,连接 .(16分)
(1) 如图①, 在 轴负半轴上,且 交 于点 、交 于点 ,求证:.
(2) 如图②,在()的条件下,连接 ,求证:.
(3) 如图③, 为 的中点, 是 轴上一个动点,连接 ,作 交 轴于 ,猜想 ,, 三条线段之间的数量关系,并说明理由.
答案
1-12 DADDC BCADB CB
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
17. 【答案】 ,
18. 【答案】
(1) 去分母得:解得:经检验 是增根,分式方程无解.
(2) 去分母得:去括号得:移项合并得:解得:经检验 是分式方程的解.
19. 【答案】
(1) 设 型芯片的单价为 元/条,则 型芯片的单价为 元/条,
根据题意得:解得:经检验, 是原方程的解,且符合题意.
.
答: 型芯片的单价为 元/条, 型芯片的单价为 元/条.
(2) 设购买 条 型芯片,则购买 条 型芯片,
根据题意得:解得:答:购买了 条 型芯片.
20. 【答案】
(1)
(2)
(3) 画出图形如图,在 上截取 ,连接 .
,,
,
.
,
,
.
,,
,,
.
,,
,
,
,
,
.
21. 【答案】
(1) ,,
,
,,
,
,
在 和 中,
.
(2) 如图,过点 作 ,,
,,
,
在 和 中,
,
,
,,,
平分 ,
.
(3) .
如图,连 ,
,,
,
,,
,
,
在 和 中,
,
,
.
同课章节目录
