发现潜藏的逻辑谬误 课件(共50张PPT)
文档属性
| 名称 | 发现潜藏的逻辑谬误 课件(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 统编版 | ||
| 科目 | 语文 | ||
| 更新时间 | 2023-01-23 17:40:53 | ||
图片预览











文档简介
(共50张PPT)
逻辑的力量
发现逻辑背后的谬误
下列话语中的“逻辑”是指什么
生物界遵循优胜劣汰、适者生存的逻辑。
我很难相信平行宇宙那一套逻辑。
他说的这番话完全不合逻辑。
福尔摩斯精通逻辑。
逻辑是一门独立的学问,大家都要学一点儿。
明确:在本单元中要学的逻辑是指思维的规律和推理、论证的本领。
(指规律、事理。)
(指道理、理论。)
(指思维的规律。)
(指推理和论证的本领。)
(指研究思维的形式和规律,研究推理和论证的科学——逻辑学。)
含义:心理学上认为,概念是人脑对客观事物本质的反映,这种反映是以词来标示和记载的。概念是思维活动的结果和产物,同时又是思维活动借以进行的单元。
一、何为“概念”
一、概 念
概念
内涵:
外延:
概念所反映的思维对象的本质特有的属性的总和。
概念所概括的思维对象的数量和范围。
一、概 念
解读概念的“内涵”
本质特征
个性
解读概念的“外延”
共性
一、概 念
一个概念的内涵越多,外延就越小,反之,内涵越少,外延就越大。这就是内涵与外延的反比关系。
“钢笔”这个概念的内涵,比“笔”的内涵要多。
“钢笔”有笔的一般特点外,还增加了“笔尖用金属制成,钢性的,用墨水书写”这一特点。
“钢笔”的外延比“笔”的外延要小,它把毛笔、铅笔、圆珠笔等都排除在外。
一、概 念
概念间的关系
全同关系
包含关系
交叉关系
矛盾关系
反对关系
如:“偷”与“窃”;“母亲”与“妈妈”
如:“马”与“白马”;“学生”与“中学生”
如:“教师”与“作家”;“青年”与“医生”
如:“战争”与“和平”;“真理”与“谬论”
如:“冠军”与“季军”
a
b
a
b
a
b
a
b
a
b
全同关系
包含关系
交叉关系
矛盾关系
反对关系
相容关系
全同关系”就是两个概念的外延完全相同。
包含关系”中一个概念是另一个概念的一部分。
“交叉关系”就是两个概念的外延有相同的部分,也有不同的部分。
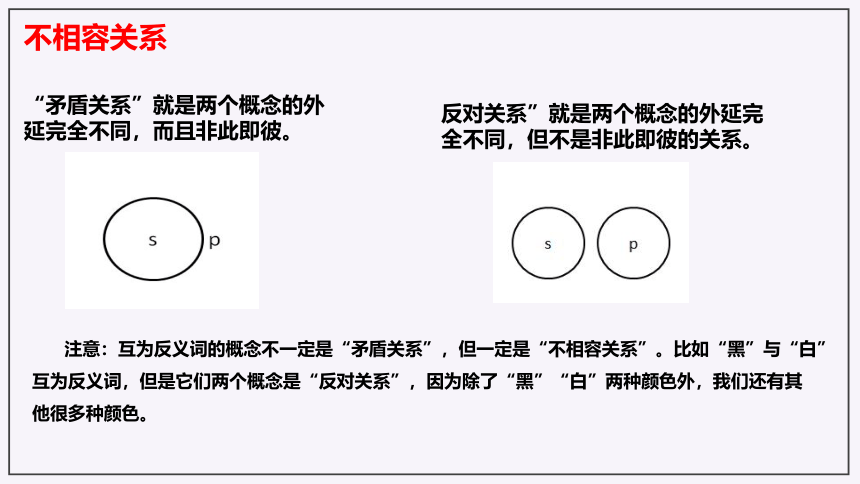
“矛盾关系”就是两个概念的外延完全不同,而且非此即彼。
不相容关系
反对关系”就是两个概念的外延完全不同,但不是非此即彼的关系。
注意:互为反义词的概念不一定是“矛盾关系”,但一定是“不相容关系”。比如“黑”与“白”互为反义词,但是它们两个概念是“反对关系”,因为除了“黑”“白”两种颜色外,我们还有其他很多种颜色。
二、命题
表达判断的句子。
定义:是运用概念进行判断的语言形式,是断定或陈述事物情况的思维单位。
如:① 中国革命是世界革命的一部分。
②李白和杜甫是同时代人。
明确逻辑规律 、发现逻辑谬误
女孩对男孩说:“我说一句关于你的话,如果对了,你告诉我这道题的答案,可以吗?”男孩想:“反正不管你说什么,我都说是错的。”但是女孩说完这句话后,男孩绞尽脑汁也想不出拒绝的方法,只好告诉女孩这道题的答案。
猜猜女孩说了什么?从逻辑上分析女孩这样说的原因。
女孩儿说:你不会把答案告诉我。
男孩有两种选择:说出题答案与不说题答案。
如果不说,则女孩说的就是事实,那么按照约定,男孩就得说出答案。即男孩无论做哪种选择都必须说出答案。
女孩对男孩说:“我说一句关于你的话,如果对了,你告诉我这道题的答案,可以吗?”男孩想:“反正不管你说什么,我都说是错的。”但是女孩说完这句话后,男孩绞尽脑汁也想不出拒绝的方法,只好告诉女孩这道题的答案。
猜猜女孩说了什么?从逻辑上分析女孩这样说的原因
第一种情况
女孩的回答:你不会把答案告诉我。(男孩的这正确答案:反正不管你说什么,我都说是错的。)
男孩:承认女孩说对了(男孩女孩有协议在先,女孩答案正确,依据协议男孩就告诉女孩这道题题的答案)
第二种情况
女孩的答案:你不会把答案告诉我。男孩:认为女孩说错了
答案错误,暗含事实是男孩会把答案告诉女孩。
(女孩说的“你不会把答案告诉我。”,与之相对的就是---你会把答案告诉我)
要么说出答案,要么不说,二者必居其一,这是排中律。
男孩如果不说答案,那就必须说答案,这是逻辑最不能容忍的一类现象——矛盾;任何一种观点都不能和自身的否定并存,这是逻辑不矛盾律。
看来男孩也是敬畏逻辑和信守承诺的。相信他给出的答案一定就是女孩所要的那道题的答案,这体现逻辑同一律。
男孩最终告知答案的决定,是建立在双方约定的规则以及女孩说出的话的基础之上,并经由严格的推理得出的。前提为真,推理合乎逻辑,这是逻辑的第四条规律——充足理由律。
逻辑的基本规律:
同一律
不矛盾律(矛盾律)
排中律
充足理由律
逻辑的基本规律
逻辑作为思维的规律,具有这四个基本规律——“同一律”“不矛盾律”“排中律”“充足理由律”。
“同一律”要求在同一思维过程中概念和判断具有确定性,始终保持如一。也就是概念间的关系应为“全同关系”。
“不矛盾律”要求相互否定的判断不能同真;“排中律”要求两个相互矛盾的判断必有一真。使用这两个规律时,概念间的关系应为“矛盾关系”,互为“矛盾关系”的两个概念不能同真但必有一真,也就是一定是一真一假。
“充足理由律”要求一个被断定为真的判断具备充足的理由。一个概念是另一个概念的原因,但结果的出现一定要有充足的理由。
01 同一律
同一律:在同一思维过程中的概念和命题都要始终保持一致,不得随意变更, 即A就是A。
概念同一:概念的内涵和外延必须保持一致。
命题同一:命题自身的意思和真假必须保持同一。
例如,“杜鹃”这一概念,有三种含义。但在同一思维过程中,“杜鹃”的内涵和外延应该是确定的,它不能同时既指花名,又指鸟名或人名,否则会造成思维的混乱。
(1)违反同一律的逻辑错误——偷换概念
在使用概念做出判断,或者运用判断进行推理的过程中,如果违反同一律,把不同的概念当成同一个概念来使用,所犯的逻辑错误叫混淆概念,或者偷换概念。
人是由猿猴进化而来的,张三是人。因此张三是猿猴进化而来的。
违反“同一律”
“人”概念:1.一个动物种类 2.这个种类的每一个个体。
小伙子:“你老是要这要那,不怕人家说你是‘高价姑娘‘吗?“
姑娘:“怕什么!裴多菲都说了,’生命诚可贵,爱情价更高‘嘛!”
显然,这位答话的姑娘故意偷换概念。我们知道,所谓“高价姑娘”的“价”,是“价格”)的“价”。人们用“高价姑娘”来贬斥那些把爱情当作商品进行交易的姑娘。而裴多菲诗中“爱情价更高”的“价”是“价值”的“价”。这句话是在赞美真正的爱情比生命还要宝贵。因此同一个“价”字表达的是不同的概念,但上述答话的姑娘却故意将它们混同起来,用前者偷换后者,这明显是违反同一律要求的逻辑错误。
偷 换 概 念
(2)违反同一律的逻辑错误——转移论题/偷换论题
讨论的焦点转移到另一个话题,从而逃避质疑或攻击。
例:妈妈问:“儿子,这次期中考试怎么考这么差啊?”
儿子说:“妈,你怎么老是跟我过不去啊!”
例 A: 你这个人怎么不讲理啊?
B: 我没给你讲过理吗?
02 矛盾律
矛盾律(不矛盾律),指在同一思维过程中,两个互相矛盾或互相反对的判断不能同真,必有一假,即“非A即B”。
互相矛盾和互相反对。
互相矛盾:两个命题互相矛盾,是指这两个命题不能同真,也不能同假。
互相反对:两个命题互相反对,是指这两个命题不能同真,但可以同假。
小明是个男孩子。
小明是个女孩子。
这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;
小明在写语文作业。
小明在写数学作业。
这两个命题是互相反对的,不能同真,但可以同假。
a
b
a
b
矛盾关系
反对关系
违反矛盾律的逻辑错误——自相矛盾
一个青年人很想到美国大发明家爱迪生的实验室去搞科研。经过努力,他终于见到了他所敬仰的爱迪生,很高兴地说:“我想发明一种万能溶液,它可以溶解世上的一切物品。爱迪生听后很惊奇地反问:
青年人一时语塞。
“那么你想用什么容器来装这种液体呢?”
有人主张多运动,有人不主张多运动,这两种观点我都赞同。
03 排中律
排中律
排中律指在同一思维过程中,两个互相矛盾的判断不能同假,必有一真。
区别:
排中律:必有一真 (不能同假)
只能用于两个相互矛盾的判断。
矛盾律:有一假或同假(不能同真)
两个互相矛盾的判断或两个互相反对的判断。
总结:如果是矛盾关系,那一定是一真一假。
如果是反对关系,有可能同假,有可能一真一假
a
b
矛盾关系
a
b
a
b
矛盾关系
反对关系
(1)侧重点不同:矛盾律规定互相否定的思想不能同真,必有一假;排中律规定互相矛盾的思想不能同假,必有一真。
(2)适用范围不同:矛盾律适用于“互相否定(矛盾或反对关系)的思想”;排中律只适用于“互相矛盾的思想”。排中律只适用于两个互相矛盾的判断,而不适用于两个互相反对的判断。这是因为,两个互相反对的判断可以同假,不必非得有一个为真。
(3)逻辑要求不同:矛盾律要求对互相否定的思想不得同时肯定;排中律要求对互相矛盾的思想不得同时否定。
矛盾律与排中律的区别
矛盾律与排中律的区别
排中律使用常见谬误——模棱两可
在同一思维过程中,两个互相矛盾的判断不能同真,也不能同假。如果同时肯定或否定,就犯了“两可”或“两不可”的错误,
他是这次车祸十多位遇难者中唯一幸免的人。
这篇文章的观点不能说是全面的,也不能说不全面。
我们处在奔向理想的不可逆转的潮流中——但这可能会改变。
不能同真——违反矛盾律(两可)
不能同假——违反排中律(两不可)
不能同真——违反矛盾律(两可)
排中律使用常见谬误——模棱两可
有人说冬天启动汽车需要预热一下发动机再起步行驶;有人说现在汽车技术成熟了,冬天启动汽车后不需要预热发动机,只要视野良好可立即起步行驶。这两种观点我都不赞成。
排中律使用常见谬误——假二择一
明明存在多种可能性,却说成只有两种可能,迫使对方作出自己所希望的选择,这叫“假二择一”“虚假两难”。
例:20世纪越战期间,美国一些人为反对越战的人张贴了标语:
美国:热爱它,要么离开它。
①留在美国且支持越战; ②留在美国但不支持越战;
③离开美国但支持越战; ④离开美国且不支持越战。
此标语屏蔽了②③,只给出了①④,目的在于①(且为道德绑架)
04 充足理由律
充足理由律
一个判断被断定为真必须要有充足的理由。如果没有充足理由,则该判断不能被断定为真。 即:B真,因为A真,并且A能推出B。
充足理由律使用常见谬误:
强加因果、推 不 出、没有理由、不当预设、轻率归纳、不当类比、循环论证
充足理由律使用常见谬误——强加因果
没有因果关系的事件,因为发生的时间相近等表面联系,就把它们看成是因果事件,叫作强加因果。
《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏要在这时候,——这就可见是一个谬种!”
分析:鲁迅的《祝福》中,鲁四老爷的这句话存在两个错误捆绑:一是把祥林嫂的死和祝福捆绑,二是把死和“谬种”捆绑。祥林嫂的死与年关的祝福活动,只是时间上接近的两件事,并无因果关系--不是祥林嫂自主选择或命中注定。明明没有因果关系的事件,因为发生的时间相近等表面联系,就把它们看成是因果事件,叫作强加因果,违反了充足理由律。
强加因果。一把祥林嫂的死与祝福捆绑。二是把“死”和“谬种”捆绑
强加因果
1、送来的时候还好好的,怎么到你们医院之后就不行了呢?
2、没撞,你为什么要扶?
3、小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。
推 不 出
别里科夫有一次看到他学校的同事柯瓦连科同他的姐姐华连卡在街上骑自行车,吓得脸色由青到白。第二天他到柯瓦连科家里,说:“您骑自行车,这种消遣,对青年的教育者来说,是绝对不合时宜的!”当柯瓦连科问他为什么时,他说:“难道这还用解释吗,……如果教师骑自行车,那还能希望学生做出什么好事来?他们所能做的就只有倒过来,用脑袋走路了!既然政府还没有发出通告,允许做这种事,那就做不得。”
别里科夫反对青年教育者骑自行车的理由有两个:一是“如果教师骑自行车,那还能希望学生做出什么好事来”,二是“政府还没有发出通告,允许做这种事”。这两个理由,前者是虚假的,犯了“理由虚假”的错误;后者虽然是真实的,但与“青年教育者不能骑自行车”的结论之间没有必然联系,犯了“推不出”的逻辑错误。总之,别里科夫的话违反了充足理由律。
充足理由律使用常见谬误——没有理由
① 你们不要相信他的话,他因生活作风有问题受过处分 (诉诸个人)
②我所主张的不过是大多数公众的观点,你反对我,就是在与公众作对。不信你问一问在场的人? (诉诸公众)
③我上有年迈的双目失明失去自理能力的老母,下有一个正在上小学的孩子,如果给我判刑,投入监狱,他们该怎么办呀!(诉诸怜悯)
④爱因斯坦都这么说,你竟敢不同意? (诉诸权威)
充足理由律使用常见谬误——不当预设
在问题中隐藏着前提,对方的回答无论是肯定还是否定,都意味着承认这个前提。而这个前提很有可能是虚假的。
以下是古希腊著名悲剧家索福克勒斯的悲剧《俄狄浦斯王》中俄狄浦斯的一段台词:你(克瑞翁)这人,你来干什么 你的脸皮这样厚 你分明是想谋害我,夺取我的王位,还有脸来我家吗 喂,当着众神,你说吧:你是不是把我看成了懦夫和傻子,才打算这样干 你狡猾地向我爬过来,你以为我不会发觉你的诡计,发觉了也不能提防吗 你的企图岂不是太愚蠢吗
俄狄浦斯问了一连串问题,克瑞翁都无法回答,因为他无论是答“是”还是答“否”,都等于承认了算夺王位的意图。不当预设在生活很常见。
充足理由律使用常见谬误——轻率归纳
金银铜铁受热后体积都会膨胀,因此,所有金属受热后体积都会膨胀。
前提真不一定保证结论真,尤其在考察数量少,样本不具有代表性的情况下
盘点盖茨、乔布斯、戴尔、扎克伯格等世界级富豪,辍学是他们走向成功的关键一步,这让人不得不思考正规的国民教育对创业者是否真的必要。
国民教育对创业者并不真的必要。
说话者用少部分大学或预科辍学的例子质疑整个国民教育对所有创业者的必要性,是不妥当。
充足理由律使用常见谬误——不当类比
类比推理,是根据两个或两类对象某些属性相似或相同,进而推出它们另一属性也相似或相同的推理。
A具有C属性和D属性
B具有C属性
B也具有D属性
若将两类没有可比性,“假相似”的对象进行比对,进而得出结论,这样的作法称为”不当类比”
充足理由律使用常见谬误——不当类比
太阳是被创造出来照亮地球的。人们总是移动火把去照亮房子,而不是移动房子去被火把照亮。因此,只能是太阳绕着地球转,而不是地球绕着太阳转。
类比前提:太阳和地球的关系=火把与房子的关系
但是两者并不相似。火把确实可以照亮房子,却不能说太阳是用于照亮地球的。
充足理由律使用常见谬误——循环论证
尚待证明的结论不能出现或暗含在前提中,否则就是循环论证。循环论证的本质是“因为A,所以A”
我骂(你)卖国贼,所以我是爱国者。爱国者的话是最有价值的,所以我的话是不错的,我的话既然不错,你就是卖国贼无疑了!(鲁迅《论辩的魂灵》)
商人都是唯利是图的,如果不唯利是图,那就不是商人了。
课 堂 练 习
分析下面的例子,指出其中的逻辑错误:
①鲁迅的作品不是一天能读完的,《孔乙己》是鲁迅的作品,所以,《孔乙己》不是一天能读完的。
②庄子曰:“请循其本。子曰‘汝安知鱼乐’云者,既已知吾知之而问我,我知之濠上也。
分析: 第一个“作品”是鲁迅“所有”作品的总称,第二个“作品”是“各个”作品的通称,看起来表述一样,其实不是一个概念,所以造成推理的错误。“鲁迅的作品”和“《孔乙己》”是“包含关系”,不是“全同关系”,这样的情况就是“偷换概念”,违反“同一律”。
分析:安,在问句中通常有两种用法,一种表示“怎么” ,另一种表示“在哪里”。庄子和 惠子一开始是围绕“人能不能以及怎么能知道鱼快乐”的话题进行的。但到最后,庄子突然偷换概念,把“安”用于表示“在哪里”,并以“知之濠上”作结 庄子回答的“安”是“哪里”的意思,惠子问的是“你怎么知道鱼是快乐的”,是问原因,庄子回答“是在濠上这个地方知道的”,是答地点,答非所问,违反了“同一律”。
违反同一律的逻辑错误——偷换概念、转移论题/偷换论题
违反不矛盾律(矛盾律)的逻辑错误——自相矛盾
排中律使用常见谬误——模棱两可、假二择一
充足理由律使用常见谬误:
强加因果、推 不 出、没有理由、不当预设、轻率归纳、不当类比、循环论证
课 堂 练 习
客人的意思是“手指将汤弄脏了”服务员理解成“担心烫手”,违反“同一律”。
③“服务员同志,请当心,你的手指浸到我的汤里去了。“
“没有关系,汤不烫,我不痛。”
分析:顾客想表达的是提醒甚至抗议,关注的是他的饭菜的卫生问题;服务员却把问题转移成自己有没有被烫的问题。应该说服务员的答话颇为狡黠,但考虑到其做法确实有损顾客的权益,而又有逃避责任的意思,可以认定其答话是典型的“偷换论题”的谬误,同样违反了同一律。
④“我是答应您昨天来修门铃没错。可我来了三次,每次按门铃,都没有人来开门,我只好走了。”
分析:一般来说,需要修门铃就是因为门铃坏了,又怎么能指望“每次按门铃”就“有人来开门”呢 说话人或是真的未意识到其中的问题,或是为自己的不守信而开脱,总之都犯了自相矛盾的错误,违反了不矛盾律。
课 堂 练 习
⑤在法国某地,一个耍戏法的人招揽观众:“快来快来,这里有拿破仑的头骨。”围观的一个人说:“奇怪,听说拿破仑的脑袋是很大的,这个头骨怎么和普通人的没有区别啊?”耍戏法的人解释道:“没错,这是拿破仑小时候的头骨。”
分析:“拿破仑小时候的头骨”被保留下来则意味着拿破仑死于童年。而耍戏法的用拿破仑的名号来招揽观众,显然指的是活到成年后叱咤风云的拿破仑。这个有名的拿破仑1821年5月5日(52岁)病逝于南大西洋圣赫勒拿岛,又何来“小时候的头骨” “拿破仑死于童年”和“拿破仑死于成年之后”两者必有一假,耍戏法的违反了不矛盾律。
⑥有人说,《红楼梦》值得读,有人说不值得,两种意见我都不赞成:读,太花时间;不读,又有点儿可惜。
“值得读”和“不值得读”是“相互矛盾关系”,必有一真,不能同为假,不能 都否定,都否定违反“排中律”。
课 堂 练 习
⑦不薄之谓厚,不白之谓黑。
⑧《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏在这时候,——这就可见是一个谬种!”
⑨你是否已经停止了对我的毁谤?请回答“是”或者“不是”!
分析:薄厚之间存在着中间状态,白黑之间还有灰。说话人屏蔽了中间状态,只呈现出两种端的情形,让人在两个极端之间作出判断或选择。这其实是在并非矛盾(有第三种可能存在)的情形下使用排中律,属于排中律使用不当。
用一个人的死亡时间,推测出“是一个谬种”的结论,谬种”的理由是死得不是时候,这个理由并不充足,违反“充足理由律”。
分析:“你是否已经停止了对我的毁谤”这个问题,隐藏着一个前提:对方此前一直在毁谤说话人。对方的回答无论肯定还是否定,都意味着承认这个前提。而这个前提很可能是虚假的。可以把这种错误叫作“不当预设”。违反了“充足理由律”。
10、《儒林外史》第三回中,范进中举前,胡屠户说:“不要失了你的时了!你自己只觉得中了一个相公,就‘癞虾蟆想吃起天鹅肉’来!......你不看见城里张府上那些老爷,都有万贯家私,一个个方面大耳,像你这尖嘴猴腮,也该撒抛尿自己照照!不三不四,就想天鹅屁吃!”范进中举后,胡屠户说:“我的这个贤婿,才学又高,品貌又好,就是城里头那张府、周府这些老爷,也没有我女婿这样一个体面的相貌!”
胡屠户对范进中举前后的态度自相矛盾了,违反了“不矛盾律”。
水到渠成辨谬误
违反“同一律”就会犯“偷换概念”“混淆概念”的逻辑错误,主要表现为“划分不当”“发生歧义”“以偏概全”等;违反“不矛盾律”就会犯“自相矛盾”的逻辑错误;违反“排中律”就会犯“模棱两可”的逻辑错误;违反“充足理由律”就会犯“强加因果”的逻辑错误。
所以,同学们平时还要多留心注意存在逻辑错误的话语,分析其错误的原因,明确病句除了语法性的错误外,还要注意“不合逻辑”的逻辑性病句。
课堂检测
1、我们的孩子在小学和初中成绩都很好,怎么到了你们高中就下滑了呢?
强加因果充足理由律
2、我很相信一位哲人的名言:世界上没有什么东西是可信的。
违反不矛盾律
3、蚊子战胜了狮子,狮子战胜了其他一切动物,所以,蚊子战胜了其他一切动物。
违背了充足理由律
4、你的意见既正确又全面,我毫无意见。不过,有几个地方还需要商榷一下。
违背了不矛盾律
逻辑的力量
发现逻辑背后的谬误
下列话语中的“逻辑”是指什么
生物界遵循优胜劣汰、适者生存的逻辑。
我很难相信平行宇宙那一套逻辑。
他说的这番话完全不合逻辑。
福尔摩斯精通逻辑。
逻辑是一门独立的学问,大家都要学一点儿。
明确:在本单元中要学的逻辑是指思维的规律和推理、论证的本领。
(指规律、事理。)
(指道理、理论。)
(指思维的规律。)
(指推理和论证的本领。)
(指研究思维的形式和规律,研究推理和论证的科学——逻辑学。)
含义:心理学上认为,概念是人脑对客观事物本质的反映,这种反映是以词来标示和记载的。概念是思维活动的结果和产物,同时又是思维活动借以进行的单元。
一、何为“概念”
一、概 念
概念
内涵:
外延:
概念所反映的思维对象的本质特有的属性的总和。
概念所概括的思维对象的数量和范围。
一、概 念
解读概念的“内涵”
本质特征
个性
解读概念的“外延”
共性
一、概 念
一个概念的内涵越多,外延就越小,反之,内涵越少,外延就越大。这就是内涵与外延的反比关系。
“钢笔”这个概念的内涵,比“笔”的内涵要多。
“钢笔”有笔的一般特点外,还增加了“笔尖用金属制成,钢性的,用墨水书写”这一特点。
“钢笔”的外延比“笔”的外延要小,它把毛笔、铅笔、圆珠笔等都排除在外。
一、概 念
概念间的关系
全同关系
包含关系
交叉关系
矛盾关系
反对关系
如:“偷”与“窃”;“母亲”与“妈妈”
如:“马”与“白马”;“学生”与“中学生”
如:“教师”与“作家”;“青年”与“医生”
如:“战争”与“和平”;“真理”与“谬论”
如:“冠军”与“季军”
a
b
a
b
a
b
a
b
a
b
全同关系
包含关系
交叉关系
矛盾关系
反对关系
相容关系
全同关系”就是两个概念的外延完全相同。
包含关系”中一个概念是另一个概念的一部分。
“交叉关系”就是两个概念的外延有相同的部分,也有不同的部分。
“矛盾关系”就是两个概念的外延完全不同,而且非此即彼。
不相容关系
反对关系”就是两个概念的外延完全不同,但不是非此即彼的关系。
注意:互为反义词的概念不一定是“矛盾关系”,但一定是“不相容关系”。比如“黑”与“白”互为反义词,但是它们两个概念是“反对关系”,因为除了“黑”“白”两种颜色外,我们还有其他很多种颜色。
二、命题
表达判断的句子。
定义:是运用概念进行判断的语言形式,是断定或陈述事物情况的思维单位。
如:① 中国革命是世界革命的一部分。
②李白和杜甫是同时代人。
明确逻辑规律 、发现逻辑谬误
女孩对男孩说:“我说一句关于你的话,如果对了,你告诉我这道题的答案,可以吗?”男孩想:“反正不管你说什么,我都说是错的。”但是女孩说完这句话后,男孩绞尽脑汁也想不出拒绝的方法,只好告诉女孩这道题的答案。
猜猜女孩说了什么?从逻辑上分析女孩这样说的原因。
女孩儿说:你不会把答案告诉我。
男孩有两种选择:说出题答案与不说题答案。
如果不说,则女孩说的就是事实,那么按照约定,男孩就得说出答案。即男孩无论做哪种选择都必须说出答案。
女孩对男孩说:“我说一句关于你的话,如果对了,你告诉我这道题的答案,可以吗?”男孩想:“反正不管你说什么,我都说是错的。”但是女孩说完这句话后,男孩绞尽脑汁也想不出拒绝的方法,只好告诉女孩这道题的答案。
猜猜女孩说了什么?从逻辑上分析女孩这样说的原因
第一种情况
女孩的回答:你不会把答案告诉我。(男孩的这正确答案:反正不管你说什么,我都说是错的。)
男孩:承认女孩说对了(男孩女孩有协议在先,女孩答案正确,依据协议男孩就告诉女孩这道题题的答案)
第二种情况
女孩的答案:你不会把答案告诉我。男孩:认为女孩说错了
答案错误,暗含事实是男孩会把答案告诉女孩。
(女孩说的“你不会把答案告诉我。”,与之相对的就是---你会把答案告诉我)
要么说出答案,要么不说,二者必居其一,这是排中律。
男孩如果不说答案,那就必须说答案,这是逻辑最不能容忍的一类现象——矛盾;任何一种观点都不能和自身的否定并存,这是逻辑不矛盾律。
看来男孩也是敬畏逻辑和信守承诺的。相信他给出的答案一定就是女孩所要的那道题的答案,这体现逻辑同一律。
男孩最终告知答案的决定,是建立在双方约定的规则以及女孩说出的话的基础之上,并经由严格的推理得出的。前提为真,推理合乎逻辑,这是逻辑的第四条规律——充足理由律。
逻辑的基本规律:
同一律
不矛盾律(矛盾律)
排中律
充足理由律
逻辑的基本规律
逻辑作为思维的规律,具有这四个基本规律——“同一律”“不矛盾律”“排中律”“充足理由律”。
“同一律”要求在同一思维过程中概念和判断具有确定性,始终保持如一。也就是概念间的关系应为“全同关系”。
“不矛盾律”要求相互否定的判断不能同真;“排中律”要求两个相互矛盾的判断必有一真。使用这两个规律时,概念间的关系应为“矛盾关系”,互为“矛盾关系”的两个概念不能同真但必有一真,也就是一定是一真一假。
“充足理由律”要求一个被断定为真的判断具备充足的理由。一个概念是另一个概念的原因,但结果的出现一定要有充足的理由。
01 同一律
同一律:在同一思维过程中的概念和命题都要始终保持一致,不得随意变更, 即A就是A。
概念同一:概念的内涵和外延必须保持一致。
命题同一:命题自身的意思和真假必须保持同一。
例如,“杜鹃”这一概念,有三种含义。但在同一思维过程中,“杜鹃”的内涵和外延应该是确定的,它不能同时既指花名,又指鸟名或人名,否则会造成思维的混乱。
(1)违反同一律的逻辑错误——偷换概念
在使用概念做出判断,或者运用判断进行推理的过程中,如果违反同一律,把不同的概念当成同一个概念来使用,所犯的逻辑错误叫混淆概念,或者偷换概念。
人是由猿猴进化而来的,张三是人。因此张三是猿猴进化而来的。
违反“同一律”
“人”概念:1.一个动物种类 2.这个种类的每一个个体。
小伙子:“你老是要这要那,不怕人家说你是‘高价姑娘‘吗?“
姑娘:“怕什么!裴多菲都说了,’生命诚可贵,爱情价更高‘嘛!”
显然,这位答话的姑娘故意偷换概念。我们知道,所谓“高价姑娘”的“价”,是“价格”)的“价”。人们用“高价姑娘”来贬斥那些把爱情当作商品进行交易的姑娘。而裴多菲诗中“爱情价更高”的“价”是“价值”的“价”。这句话是在赞美真正的爱情比生命还要宝贵。因此同一个“价”字表达的是不同的概念,但上述答话的姑娘却故意将它们混同起来,用前者偷换后者,这明显是违反同一律要求的逻辑错误。
偷 换 概 念
(2)违反同一律的逻辑错误——转移论题/偷换论题
讨论的焦点转移到另一个话题,从而逃避质疑或攻击。
例:妈妈问:“儿子,这次期中考试怎么考这么差啊?”
儿子说:“妈,你怎么老是跟我过不去啊!”
例 A: 你这个人怎么不讲理啊?
B: 我没给你讲过理吗?
02 矛盾律
矛盾律(不矛盾律),指在同一思维过程中,两个互相矛盾或互相反对的判断不能同真,必有一假,即“非A即B”。
互相矛盾和互相反对。
互相矛盾:两个命题互相矛盾,是指这两个命题不能同真,也不能同假。
互相反对:两个命题互相反对,是指这两个命题不能同真,但可以同假。
小明是个男孩子。
小明是个女孩子。
这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;
小明在写语文作业。
小明在写数学作业。
这两个命题是互相反对的,不能同真,但可以同假。
a
b
a
b
矛盾关系
反对关系
违反矛盾律的逻辑错误——自相矛盾
一个青年人很想到美国大发明家爱迪生的实验室去搞科研。经过努力,他终于见到了他所敬仰的爱迪生,很高兴地说:“我想发明一种万能溶液,它可以溶解世上的一切物品。爱迪生听后很惊奇地反问:
青年人一时语塞。
“那么你想用什么容器来装这种液体呢?”
有人主张多运动,有人不主张多运动,这两种观点我都赞同。
03 排中律
排中律
排中律指在同一思维过程中,两个互相矛盾的判断不能同假,必有一真。
区别:
排中律:必有一真 (不能同假)
只能用于两个相互矛盾的判断。
矛盾律:有一假或同假(不能同真)
两个互相矛盾的判断或两个互相反对的判断。
总结:如果是矛盾关系,那一定是一真一假。
如果是反对关系,有可能同假,有可能一真一假
a
b
矛盾关系
a
b
a
b
矛盾关系
反对关系
(1)侧重点不同:矛盾律规定互相否定的思想不能同真,必有一假;排中律规定互相矛盾的思想不能同假,必有一真。
(2)适用范围不同:矛盾律适用于“互相否定(矛盾或反对关系)的思想”;排中律只适用于“互相矛盾的思想”。排中律只适用于两个互相矛盾的判断,而不适用于两个互相反对的判断。这是因为,两个互相反对的判断可以同假,不必非得有一个为真。
(3)逻辑要求不同:矛盾律要求对互相否定的思想不得同时肯定;排中律要求对互相矛盾的思想不得同时否定。
矛盾律与排中律的区别
矛盾律与排中律的区别
排中律使用常见谬误——模棱两可
在同一思维过程中,两个互相矛盾的判断不能同真,也不能同假。如果同时肯定或否定,就犯了“两可”或“两不可”的错误,
他是这次车祸十多位遇难者中唯一幸免的人。
这篇文章的观点不能说是全面的,也不能说不全面。
我们处在奔向理想的不可逆转的潮流中——但这可能会改变。
不能同真——违反矛盾律(两可)
不能同假——违反排中律(两不可)
不能同真——违反矛盾律(两可)
排中律使用常见谬误——模棱两可
有人说冬天启动汽车需要预热一下发动机再起步行驶;有人说现在汽车技术成熟了,冬天启动汽车后不需要预热发动机,只要视野良好可立即起步行驶。这两种观点我都不赞成。
排中律使用常见谬误——假二择一
明明存在多种可能性,却说成只有两种可能,迫使对方作出自己所希望的选择,这叫“假二择一”“虚假两难”。
例:20世纪越战期间,美国一些人为反对越战的人张贴了标语:
美国:热爱它,要么离开它。
①留在美国且支持越战; ②留在美国但不支持越战;
③离开美国但支持越战; ④离开美国且不支持越战。
此标语屏蔽了②③,只给出了①④,目的在于①(且为道德绑架)
04 充足理由律
充足理由律
一个判断被断定为真必须要有充足的理由。如果没有充足理由,则该判断不能被断定为真。 即:B真,因为A真,并且A能推出B。
充足理由律使用常见谬误:
强加因果、推 不 出、没有理由、不当预设、轻率归纳、不当类比、循环论证
充足理由律使用常见谬误——强加因果
没有因果关系的事件,因为发生的时间相近等表面联系,就把它们看成是因果事件,叫作强加因果。
《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏要在这时候,——这就可见是一个谬种!”
分析:鲁迅的《祝福》中,鲁四老爷的这句话存在两个错误捆绑:一是把祥林嫂的死和祝福捆绑,二是把死和“谬种”捆绑。祥林嫂的死与年关的祝福活动,只是时间上接近的两件事,并无因果关系--不是祥林嫂自主选择或命中注定。明明没有因果关系的事件,因为发生的时间相近等表面联系,就把它们看成是因果事件,叫作强加因果,违反了充足理由律。
强加因果。一把祥林嫂的死与祝福捆绑。二是把“死”和“谬种”捆绑
强加因果
1、送来的时候还好好的,怎么到你们医院之后就不行了呢?
2、没撞,你为什么要扶?
3、小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。
推 不 出
别里科夫有一次看到他学校的同事柯瓦连科同他的姐姐华连卡在街上骑自行车,吓得脸色由青到白。第二天他到柯瓦连科家里,说:“您骑自行车,这种消遣,对青年的教育者来说,是绝对不合时宜的!”当柯瓦连科问他为什么时,他说:“难道这还用解释吗,……如果教师骑自行车,那还能希望学生做出什么好事来?他们所能做的就只有倒过来,用脑袋走路了!既然政府还没有发出通告,允许做这种事,那就做不得。”
别里科夫反对青年教育者骑自行车的理由有两个:一是“如果教师骑自行车,那还能希望学生做出什么好事来”,二是“政府还没有发出通告,允许做这种事”。这两个理由,前者是虚假的,犯了“理由虚假”的错误;后者虽然是真实的,但与“青年教育者不能骑自行车”的结论之间没有必然联系,犯了“推不出”的逻辑错误。总之,别里科夫的话违反了充足理由律。
充足理由律使用常见谬误——没有理由
① 你们不要相信他的话,他因生活作风有问题受过处分 (诉诸个人)
②我所主张的不过是大多数公众的观点,你反对我,就是在与公众作对。不信你问一问在场的人? (诉诸公众)
③我上有年迈的双目失明失去自理能力的老母,下有一个正在上小学的孩子,如果给我判刑,投入监狱,他们该怎么办呀!(诉诸怜悯)
④爱因斯坦都这么说,你竟敢不同意? (诉诸权威)
充足理由律使用常见谬误——不当预设
在问题中隐藏着前提,对方的回答无论是肯定还是否定,都意味着承认这个前提。而这个前提很有可能是虚假的。
以下是古希腊著名悲剧家索福克勒斯的悲剧《俄狄浦斯王》中俄狄浦斯的一段台词:你(克瑞翁)这人,你来干什么 你的脸皮这样厚 你分明是想谋害我,夺取我的王位,还有脸来我家吗 喂,当着众神,你说吧:你是不是把我看成了懦夫和傻子,才打算这样干 你狡猾地向我爬过来,你以为我不会发觉你的诡计,发觉了也不能提防吗 你的企图岂不是太愚蠢吗
俄狄浦斯问了一连串问题,克瑞翁都无法回答,因为他无论是答“是”还是答“否”,都等于承认了算夺王位的意图。不当预设在生活很常见。
充足理由律使用常见谬误——轻率归纳
金银铜铁受热后体积都会膨胀,因此,所有金属受热后体积都会膨胀。
前提真不一定保证结论真,尤其在考察数量少,样本不具有代表性的情况下
盘点盖茨、乔布斯、戴尔、扎克伯格等世界级富豪,辍学是他们走向成功的关键一步,这让人不得不思考正规的国民教育对创业者是否真的必要。
国民教育对创业者并不真的必要。
说话者用少部分大学或预科辍学的例子质疑整个国民教育对所有创业者的必要性,是不妥当。
充足理由律使用常见谬误——不当类比
类比推理,是根据两个或两类对象某些属性相似或相同,进而推出它们另一属性也相似或相同的推理。
A具有C属性和D属性
B具有C属性
B也具有D属性
若将两类没有可比性,“假相似”的对象进行比对,进而得出结论,这样的作法称为”不当类比”
充足理由律使用常见谬误——不当类比
太阳是被创造出来照亮地球的。人们总是移动火把去照亮房子,而不是移动房子去被火把照亮。因此,只能是太阳绕着地球转,而不是地球绕着太阳转。
类比前提:太阳和地球的关系=火把与房子的关系
但是两者并不相似。火把确实可以照亮房子,却不能说太阳是用于照亮地球的。
充足理由律使用常见谬误——循环论证
尚待证明的结论不能出现或暗含在前提中,否则就是循环论证。循环论证的本质是“因为A,所以A”
我骂(你)卖国贼,所以我是爱国者。爱国者的话是最有价值的,所以我的话是不错的,我的话既然不错,你就是卖国贼无疑了!(鲁迅《论辩的魂灵》)
商人都是唯利是图的,如果不唯利是图,那就不是商人了。
课 堂 练 习
分析下面的例子,指出其中的逻辑错误:
①鲁迅的作品不是一天能读完的,《孔乙己》是鲁迅的作品,所以,《孔乙己》不是一天能读完的。
②庄子曰:“请循其本。子曰‘汝安知鱼乐’云者,既已知吾知之而问我,我知之濠上也。
分析: 第一个“作品”是鲁迅“所有”作品的总称,第二个“作品”是“各个”作品的通称,看起来表述一样,其实不是一个概念,所以造成推理的错误。“鲁迅的作品”和“《孔乙己》”是“包含关系”,不是“全同关系”,这样的情况就是“偷换概念”,违反“同一律”。
分析:安,在问句中通常有两种用法,一种表示“怎么” ,另一种表示“在哪里”。庄子和 惠子一开始是围绕“人能不能以及怎么能知道鱼快乐”的话题进行的。但到最后,庄子突然偷换概念,把“安”用于表示“在哪里”,并以“知之濠上”作结 庄子回答的“安”是“哪里”的意思,惠子问的是“你怎么知道鱼是快乐的”,是问原因,庄子回答“是在濠上这个地方知道的”,是答地点,答非所问,违反了“同一律”。
违反同一律的逻辑错误——偷换概念、转移论题/偷换论题
违反不矛盾律(矛盾律)的逻辑错误——自相矛盾
排中律使用常见谬误——模棱两可、假二择一
充足理由律使用常见谬误:
强加因果、推 不 出、没有理由、不当预设、轻率归纳、不当类比、循环论证
课 堂 练 习
客人的意思是“手指将汤弄脏了”服务员理解成“担心烫手”,违反“同一律”。
③“服务员同志,请当心,你的手指浸到我的汤里去了。“
“没有关系,汤不烫,我不痛。”
分析:顾客想表达的是提醒甚至抗议,关注的是他的饭菜的卫生问题;服务员却把问题转移成自己有没有被烫的问题。应该说服务员的答话颇为狡黠,但考虑到其做法确实有损顾客的权益,而又有逃避责任的意思,可以认定其答话是典型的“偷换论题”的谬误,同样违反了同一律。
④“我是答应您昨天来修门铃没错。可我来了三次,每次按门铃,都没有人来开门,我只好走了。”
分析:一般来说,需要修门铃就是因为门铃坏了,又怎么能指望“每次按门铃”就“有人来开门”呢 说话人或是真的未意识到其中的问题,或是为自己的不守信而开脱,总之都犯了自相矛盾的错误,违反了不矛盾律。
课 堂 练 习
⑤在法国某地,一个耍戏法的人招揽观众:“快来快来,这里有拿破仑的头骨。”围观的一个人说:“奇怪,听说拿破仑的脑袋是很大的,这个头骨怎么和普通人的没有区别啊?”耍戏法的人解释道:“没错,这是拿破仑小时候的头骨。”
分析:“拿破仑小时候的头骨”被保留下来则意味着拿破仑死于童年。而耍戏法的用拿破仑的名号来招揽观众,显然指的是活到成年后叱咤风云的拿破仑。这个有名的拿破仑1821年5月5日(52岁)病逝于南大西洋圣赫勒拿岛,又何来“小时候的头骨” “拿破仑死于童年”和“拿破仑死于成年之后”两者必有一假,耍戏法的违反了不矛盾律。
⑥有人说,《红楼梦》值得读,有人说不值得,两种意见我都不赞成:读,太花时间;不读,又有点儿可惜。
“值得读”和“不值得读”是“相互矛盾关系”,必有一真,不能同为假,不能 都否定,都否定违反“排中律”。
课 堂 练 习
⑦不薄之谓厚,不白之谓黑。
⑧《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏在这时候,——这就可见是一个谬种!”
⑨你是否已经停止了对我的毁谤?请回答“是”或者“不是”!
分析:薄厚之间存在着中间状态,白黑之间还有灰。说话人屏蔽了中间状态,只呈现出两种端的情形,让人在两个极端之间作出判断或选择。这其实是在并非矛盾(有第三种可能存在)的情形下使用排中律,属于排中律使用不当。
用一个人的死亡时间,推测出“是一个谬种”的结论,谬种”的理由是死得不是时候,这个理由并不充足,违反“充足理由律”。
分析:“你是否已经停止了对我的毁谤”这个问题,隐藏着一个前提:对方此前一直在毁谤说话人。对方的回答无论肯定还是否定,都意味着承认这个前提。而这个前提很可能是虚假的。可以把这种错误叫作“不当预设”。违反了“充足理由律”。
10、《儒林外史》第三回中,范进中举前,胡屠户说:“不要失了你的时了!你自己只觉得中了一个相公,就‘癞虾蟆想吃起天鹅肉’来!......你不看见城里张府上那些老爷,都有万贯家私,一个个方面大耳,像你这尖嘴猴腮,也该撒抛尿自己照照!不三不四,就想天鹅屁吃!”范进中举后,胡屠户说:“我的这个贤婿,才学又高,品貌又好,就是城里头那张府、周府这些老爷,也没有我女婿这样一个体面的相貌!”
胡屠户对范进中举前后的态度自相矛盾了,违反了“不矛盾律”。
水到渠成辨谬误
违反“同一律”就会犯“偷换概念”“混淆概念”的逻辑错误,主要表现为“划分不当”“发生歧义”“以偏概全”等;违反“不矛盾律”就会犯“自相矛盾”的逻辑错误;违反“排中律”就会犯“模棱两可”的逻辑错误;违反“充足理由律”就会犯“强加因果”的逻辑错误。
所以,同学们平时还要多留心注意存在逻辑错误的话语,分析其错误的原因,明确病句除了语法性的错误外,还要注意“不合逻辑”的逻辑性病句。
课堂检测
1、我们的孩子在小学和初中成绩都很好,怎么到了你们高中就下滑了呢?
强加因果充足理由律
2、我很相信一位哲人的名言:世界上没有什么东西是可信的。
违反不矛盾律
3、蚊子战胜了狮子,狮子战胜了其他一切动物,所以,蚊子战胜了其他一切动物。
违背了充足理由律
4、你的意见既正确又全面,我毫无意见。不过,有几个地方还需要商榷一下。
违背了不矛盾律
