圆周角和圆心角的关系-----中考链接能力提升题(附答案)
文档属性
| 名称 | 圆周角和圆心角的关系-----中考链接能力提升题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 185.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-03 10:03:38 | ||
图片预览



文档简介
圆周角和圆心角的关系
-----中考链接能力提升题
一.选择题(共12小题)
1.(2013 自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A. 3 B. 4 C. 5 D. 8
2.(2013 珠海)如图, ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A. 36° B. 46° C. 27° D. 63°
3.(2013 湛江)如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
A. 25° B. 35° C. 55° D. 70°
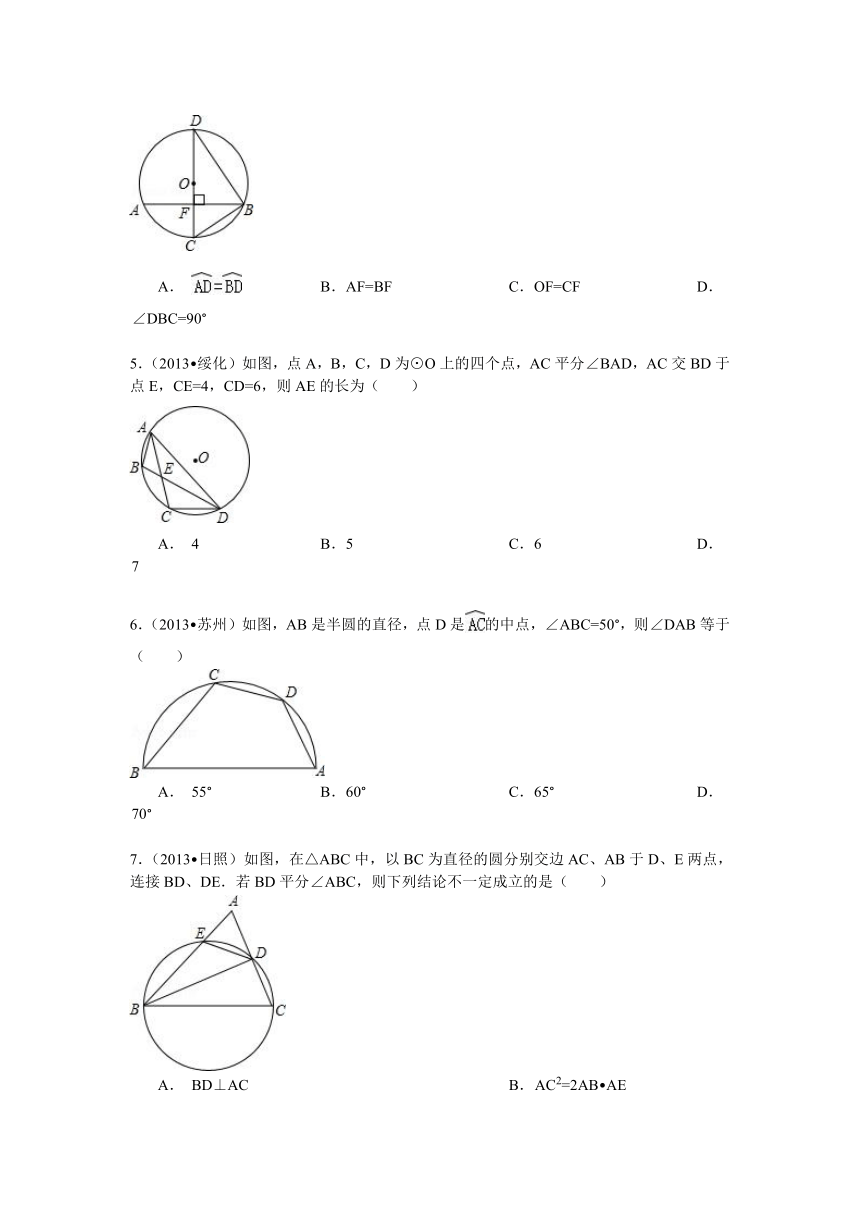
4.(2013 宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A. B. AF=BF C. OF=CF D. ∠DBC=90°
5.(2013 绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )
A. 4 B. 5 C. 6 D. 7
6.(2013 苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A. 55° B. 60° C. 65° D. 70°
7.(2013 日照)如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A. BD⊥AC B. AC2=2AB AE
C.△ADE是等腰三角形 D. BC=2AD
8.(2013 南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )
A. 4 B. 5 C. 4 D. 3
9.(2013 济南)如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为( )
A. 2 B. 3 C. 4 D. 6
10.(2013 临沂)如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是( )
A. 75° B. 60° C. 45° D. 30°
11.(2013 红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是( )
A. AD=DC B. C. ∠ADB=∠ACB D. ∠DAB=∠CBA
12.(2013 黑龙江)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
A. 3 B. 2 C. 3 D. 2
二.填空题(共6小题)
13.(2013 淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB= _________ .
14.(2013 黔西南州)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 _________ .
15.(2013 盘锦)如图,⊙O直径AB=8,∠CBD=30°,则CD= _________ .
16.(2013 常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= _________ .
17.(2012 徐州)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD= _________ .
18.(2012 泰安)如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 _________ .
三.解答题(共4小题)
19.(2013 武汉)如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°.求证:AC=AP;
(2)如图②,若sin∠BPC=,求tan∠PAB的值.
20.(2013 温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
21.(2013 哈尔滨)如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.
(1)求证:AB=AC
(2)若BD=4,BO=2,求AD的长.
22.(2012 大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.
参考答案
一.选择题(共12小题)
1. C2. A.3. B.4. C.5. B.6. C.7. D.8. B.9. C.10. B.11. D.12. A.
二.填空题(共6小题)
13. .14. 50°.15. 4.16. 2.17. .18. .
三.解答题(共4小题)
19. 解:(1)∵∠BPC=60°,∴∠BAC=60°,∵AB=AC,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,∴∠APC=∠ABC=60°,而点P是的中点,∴∠ACP=∠ACB=30°,∴∠PAC=90°,∴tan∠PCA==tan30°=,∴AC=PA;
(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,
∵AB=AC,∴AD平分BC,∴点O在AD上,连结OB,则∠BOD=∠BAC,∵∠BPC=∠BAC,∴sin∠BOD=sin∠BPC==,设OB=25x,则BD=24x,∴OD==7x,在Rt△ABD中,AD=25x+7x=32x,BD=24x,∴AB==40x,∵点P是的中点,∴OP垂直平分AB,∴AE=AB=20x,∠AEP=∠AEO=90°,在Rt△AEO中,OE==15x,∴PE=OP﹣OE=25x﹣15x=10x,在Rt△APE中,tan∠PAE===,即tan∠PAB的值为.
20.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,又∵DC=CB,∴AD=AB,∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.
21.解:(1)连接BE,CD,∵BC是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°,在Rt△ABE和Rt△ACD中,∵,∴△ABE≌△ACD,∴AB=AC.
(2)∵BO=2,∴BC=4,在Rt△BDC中,CD==8,设AD=x,则AC=AB=x+4,在Rt△ADC中,82+x2=(x+4)2,解得:x=6.即AD=6.
22.解:(1)连接BD,
∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°,∵D是AC中点,∴BD是AC的垂直平分线,∴AB=BC,∴∠A=∠C,∵∠ABC=120°,∴∠A=∠C=30°,即∠ACB=30°;
(2)过点A作AE⊥BC于点E,∵BC=3,∠ACB=30°,∠BDC=90°,∴cos30°==,∴CD=,∵AD=CD,∴AC=3,∵在Rt△AEC中,∠ACE=30°,∴AE=×3=.
-----中考链接能力提升题
一.选择题(共12小题)
1.(2013 自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A. 3 B. 4 C. 5 D. 8
2.(2013 珠海)如图, ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A. 36° B. 46° C. 27° D. 63°
3.(2013 湛江)如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
A. 25° B. 35° C. 55° D. 70°
4.(2013 宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A. B. AF=BF C. OF=CF D. ∠DBC=90°
5.(2013 绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )
A. 4 B. 5 C. 6 D. 7
6.(2013 苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A. 55° B. 60° C. 65° D. 70°
7.(2013 日照)如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A. BD⊥AC B. AC2=2AB AE
C.△ADE是等腰三角形 D. BC=2AD
8.(2013 南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )
A. 4 B. 5 C. 4 D. 3
9.(2013 济南)如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为( )
A. 2 B. 3 C. 4 D. 6
10.(2013 临沂)如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是( )
A. 75° B. 60° C. 45° D. 30°
11.(2013 红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是( )
A. AD=DC B. C. ∠ADB=∠ACB D. ∠DAB=∠CBA
12.(2013 黑龙江)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
A. 3 B. 2 C. 3 D. 2
二.填空题(共6小题)
13.(2013 淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB= _________ .
14.(2013 黔西南州)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 _________ .
15.(2013 盘锦)如图,⊙O直径AB=8,∠CBD=30°,则CD= _________ .
16.(2013 常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= _________ .
17.(2012 徐州)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD= _________ .
18.(2012 泰安)如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 _________ .
三.解答题(共4小题)
19.(2013 武汉)如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°.求证:AC=AP;
(2)如图②,若sin∠BPC=,求tan∠PAB的值.
20.(2013 温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
21.(2013 哈尔滨)如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.
(1)求证:AB=AC
(2)若BD=4,BO=2,求AD的长.
22.(2012 大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.
参考答案
一.选择题(共12小题)
1. C2. A.3. B.4. C.5. B.6. C.7. D.8. B.9. C.10. B.11. D.12. A.
二.填空题(共6小题)
13. .14. 50°.15. 4.16. 2.17. .18. .
三.解答题(共4小题)
19. 解:(1)∵∠BPC=60°,∴∠BAC=60°,∵AB=AC,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,∴∠APC=∠ABC=60°,而点P是的中点,∴∠ACP=∠ACB=30°,∴∠PAC=90°,∴tan∠PCA==tan30°=,∴AC=PA;
(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,
∵AB=AC,∴AD平分BC,∴点O在AD上,连结OB,则∠BOD=∠BAC,∵∠BPC=∠BAC,∴sin∠BOD=sin∠BPC==,设OB=25x,则BD=24x,∴OD==7x,在Rt△ABD中,AD=25x+7x=32x,BD=24x,∴AB==40x,∵点P是的中点,∴OP垂直平分AB,∴AE=AB=20x,∠AEP=∠AEO=90°,在Rt△AEO中,OE==15x,∴PE=OP﹣OE=25x﹣15x=10x,在Rt△APE中,tan∠PAE===,即tan∠PAB的值为.
20.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,又∵DC=CB,∴AD=AB,∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.
21.解:(1)连接BE,CD,∵BC是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°,在Rt△ABE和Rt△ACD中,∵,∴△ABE≌△ACD,∴AB=AC.
(2)∵BO=2,∴BC=4,在Rt△BDC中,CD==8,设AD=x,则AC=AB=x+4,在Rt△ADC中,82+x2=(x+4)2,解得:x=6.即AD=6.
22.解:(1)连接BD,
∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°,∵D是AC中点,∴BD是AC的垂直平分线,∴AB=BC,∴∠A=∠C,∵∠ABC=120°,∴∠A=∠C=30°,即∠ACB=30°;
(2)过点A作AE⊥BC于点E,∵BC=3,∠ACB=30°,∠BDC=90°,∴cos30°==,∴CD=,∵AD=CD,∴AC=3,∵在Rt△AEC中,∠ACE=30°,∴AE=×3=.
