高二数学人教A版2019选择性必修第三册 8.1 成对数据的统计相关性(分层练习)(含解析)
文档属性
| 名称 | 高二数学人教A版2019选择性必修第三册 8.1 成对数据的统计相关性(分层练习)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-24 07:46:49 | ||
图片预览



文档简介
8.1 成对数据的统计相关性
基 础 练
巩固新知 夯实基础
1.(多选)在下列各图中,两个变量具有线性相关关系的图是( )
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r43.对于线性相关系数r,叙述正确的是( )
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
4.有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如表:
平均气温/℃ -2 -3 -5 -6
销售额/万元 20 23 27 30
则该商品销售额与平均气温有( )
A.无任何关系 B.正相关关系
C.负相关关系 D.函数关系
5.观察下列关于两个变量x和y的三个散点图,它们从左到右的对应关系依次为( )
A.正相关、负相关、不相关 B.负相关、不相关、正相关
C.负相关、正相关、不相关 D.正相关、不相关、负相关
6.某公司在2019年上半年的收入x(单位:万元)与月支出y(单位:万元)的统计资料如表所示:
月份 1月 2月 3月 4月 5月 6月
收入x 12.3 14.5 15.0 17.0 19.8 20.6
支出y 5.63 5.75 5.82 5.89 6.11 6.18
根据统计资料,则( )
A.月收入的中位数是15,x与y有正线性相关关系
B.月收入的中位数是17,x与y有负线性相关关系
C.月收入的中位数是16,x与y有正线性相关关系
D.月收入的中位数是16,x与y有负线性相关关系
7.下列两个变量之间具有相关关系的是________.(填序号)
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
8.如图所示,有5组数据:A,B,C,D,E,去掉 组数据后剩下的4组数据的线性相关系数最大.
9.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系 若有,判断相关性的强弱.
能 力 练
综合应用 核心素养
10.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
11.对变量x,y由观测数据得散点图1;对变量y,z由观测数据得散点图2.由这两个散点图可以判断 ( )
A.变量x与y正相关,x与z正相关 B.变量x与y正相关,x与z负相关
C.变量x与y负相关,x与z正相关 D.变量x与y负相关,x与z负相关
12.有以下五组变量:
①某商品的销售价格与销售量;②学生的学籍号与学生的数学成绩;③坚持每天吃早餐的人数与患胃病的人数;④气温与冷饮销售量;⑤电瓶车的质量和行驶每千米的耗电量.
其中两个变量成正相关的是( )
A.①③ B.②④ C.②⑤ D.④⑤
13.(多选)某旅游景点2019年1月至9月每月最低气温与最高气温(单位:℃)的折线图如图,则下列说法正确的是( )
A.1月到9月中,最高气温与最低气温相差最大的是4月
B.1月到9月的最高气温与月份具有比较好的线性相关关系
C.最高气温与最低气温的差逐步减小
D.最低气温与最高气温间存在较好的正相关关系
14.对两个变量x,y进行分析,计算得到相关系数r=-0.9962,则下列说法中正确的是( )
A.x与y为正相关
B.x与y具有较强的线性相关关系
C.x与y几乎不具有线性相关关系
D.x与y的线性相关关系还需进一步确定
15.据两个变量x,y之间的观测数据画成散点图如图,这两个变量是否具有线性相关关系 (答是或否).
16.对相关系数r,
①r越大,线性相关程度越大;②r越小,线性相关程度越大;③|r|越大,线性相关程度越小,|r|越接近0,线性相关程度越大;④|r|≤1且|r|越接近1,线性相关程度越大,|r|越接近0,线性相关程度越小.
以上说法中,正确说法的序号是 .
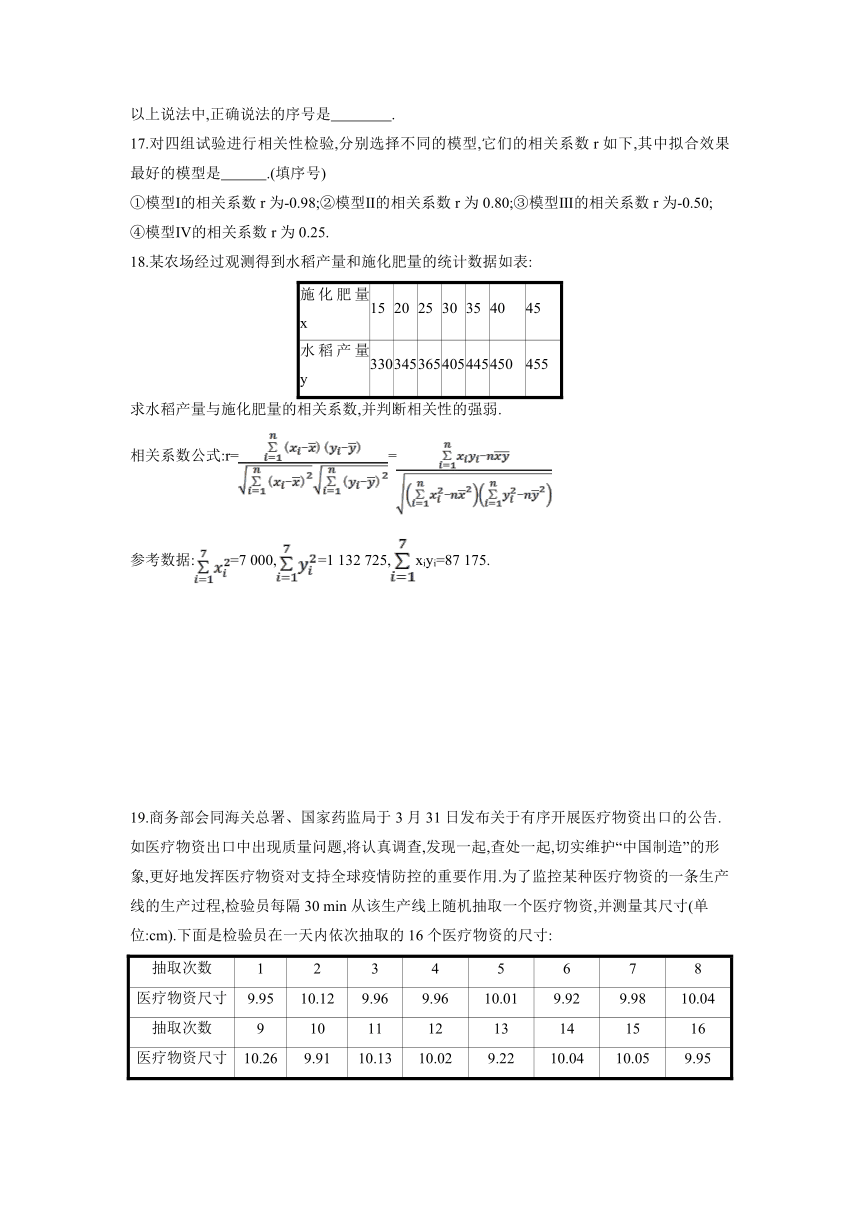
17.对四组试验进行相关性检验,分别选择不同的模型,它们的相关系数r如下,其中拟合效果最好的模型是 .(填序号)
①模型Ⅰ的相关系数r为-0.98;②模型Ⅱ的相关系数r为0.80;③模型Ⅲ的相关系数r为-0.50;
④模型Ⅳ的相关系数r为0.25.
18.某农场经过观测得到水稻产量和施化肥量的统计数据如表:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
求水稻产量与施化肥量的相关系数,并判断相关性的强弱.
相关系数公式:r==
参考数据:=7 000,=1 132 725,xiyi=87 175.
19.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取次数 1 2 3 4 5 6 7 8
医疗物资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次数 9 10 11 12 13 14 15 16
医疗物资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=.
【参考答案】
1.BC 解析:A中两个变量为函数关系,不是线性相关关系,所以A错误;B中两个变量有明显的正相关,所以具有线性相关性,所以B正确;C中两个变量有明显的负相关,所以具有线性相关性,所以C正确;D中两个变量不具有相关性,所以D错误.
2.C解析:根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;故r1>0,r3>0;r2<0,r4<0;又(1)与(2)中散点图更接近于一条直线,故r1>r3,r23.C解析:用相关系数r可以衡量两个变量之间的相关关系的强弱,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值接近于0时,表示两个变量之间几乎不存在相关关系.
4.C解析:由表中数据可知:y随x的减小而增大,是负相关关系.
5.D解析:有相关性可知从左到右的第一个图是正相关,第二个图相关性不明确,所以不相关,第三个图是负相关.
6.C解析:月收入的中位数是=16,收入增加,支出增加,故x与y有正线性相关关系.
7. ②④解析:对于①,正方形的边长a和面积S是函数关系,不是相关关系;对于②,一般情况下,一个人的身高h和右手一拃长x是正相关关系;对于③,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系;对于④,一般情况下,一个人的身高h和他的体重x是正相关关系.
8. C解析:仔细观察点A,B,C,D(7,10),E,可知点ABDE在一条直线附近,而C点明显偏离此直线,由此可知去掉点C后,使剩下的四点组成的数组相关系数最大.
9. 解:画出散点图如图所示,由图可知x,Y有线性关系.
=5,=47.5,=120,=9 900,xiyi=1 080,r=
=≈0.982 7.
故x与Y之间具有很强的正相关关系.
10.C 解析:由线性相关系数r1=0.785 9>0知x与y正相关,由线性相关系数r2=-0.956 8<0知u,v负相关,又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强.
11.D解析:由这两个散点图可以判断,变量x与y为负相关,y与z为正相关,所以x与z为负相关.
12.D解析:对于①,一般情况下,某商品的销售价格与销售量是负相关关系;
对于②,学生的学籍号与学生的数学成绩没有相关关系;
对于③,一般情况下,坚持每天吃早餐的人数与患胃病的人数是负相关关系;
对于④,一般情况下,气温与冷饮销售量是正相关关系;
对于⑤,一般情况下,电瓶车的质量和行驶每千米的耗电量是正相关关系.
13.BD解析:A选项1月到9月中,最高气温与最低气温相差最大的是1月,错误;
B选项1月到9月的最高气温与月份具有比较好的线性相关关系,正确;
C选项最高气温与最低气温的差不稳定,错误;
D选项最低气温与最高气温间存在较好的正相关关系,正确.
14.B解析:x与y为负相关,非常接近1,所以相关性很强.
15. 否 解析:由散点图可知,散点图分布无任何规律,不在一条直线附近,所以,这两个变量没有线性相关关系.
16. ④ 解析:两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强;r的绝对值非常接近于0时,表示两个变量之间几乎不存在线性相关性.
17.①解析:相关系数的正负表明两个变量是正相关还是负相关,相关系数大于零正相关,小于零负相关,相关系数的绝对值越大,相关性越强.故①的拟合效果最好.
18. 解:==30,==,
故r==≈≈0.97,故具有很强的相关性.
19.解:(1)由样本数据得(x,i)(i=1,2,3,…,16)的相关系数为
r==≈-0.18;
由于|r|<0.25,因此可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小.
(2)由于=9.97,s≈0.212,由样本数据可以看出抽取的第13个零件的尺寸在(-3s,+3s)以外,因此需对当天的生产过程进行检查.
基 础 练
巩固新知 夯实基础
1.(多选)在下列各图中,两个变量具有线性相关关系的图是( )
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r4
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
4.有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如表:
平均气温/℃ -2 -3 -5 -6
销售额/万元 20 23 27 30
则该商品销售额与平均气温有( )
A.无任何关系 B.正相关关系
C.负相关关系 D.函数关系
5.观察下列关于两个变量x和y的三个散点图,它们从左到右的对应关系依次为( )
A.正相关、负相关、不相关 B.负相关、不相关、正相关
C.负相关、正相关、不相关 D.正相关、不相关、负相关
6.某公司在2019年上半年的收入x(单位:万元)与月支出y(单位:万元)的统计资料如表所示:
月份 1月 2月 3月 4月 5月 6月
收入x 12.3 14.5 15.0 17.0 19.8 20.6
支出y 5.63 5.75 5.82 5.89 6.11 6.18
根据统计资料,则( )
A.月收入的中位数是15,x与y有正线性相关关系
B.月收入的中位数是17,x与y有负线性相关关系
C.月收入的中位数是16,x与y有正线性相关关系
D.月收入的中位数是16,x与y有负线性相关关系
7.下列两个变量之间具有相关关系的是________.(填序号)
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
8.如图所示,有5组数据:A,B,C,D,E,去掉 组数据后剩下的4组数据的线性相关系数最大.
9.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系 若有,判断相关性的强弱.
能 力 练
综合应用 核心素养
10.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
11.对变量x,y由观测数据得散点图1;对变量y,z由观测数据得散点图2.由这两个散点图可以判断 ( )
A.变量x与y正相关,x与z正相关 B.变量x与y正相关,x与z负相关
C.变量x与y负相关,x与z正相关 D.变量x与y负相关,x与z负相关
12.有以下五组变量:
①某商品的销售价格与销售量;②学生的学籍号与学生的数学成绩;③坚持每天吃早餐的人数与患胃病的人数;④气温与冷饮销售量;⑤电瓶车的质量和行驶每千米的耗电量.
其中两个变量成正相关的是( )
A.①③ B.②④ C.②⑤ D.④⑤
13.(多选)某旅游景点2019年1月至9月每月最低气温与最高气温(单位:℃)的折线图如图,则下列说法正确的是( )
A.1月到9月中,最高气温与最低气温相差最大的是4月
B.1月到9月的最高气温与月份具有比较好的线性相关关系
C.最高气温与最低气温的差逐步减小
D.最低气温与最高气温间存在较好的正相关关系
14.对两个变量x,y进行分析,计算得到相关系数r=-0.9962,则下列说法中正确的是( )
A.x与y为正相关
B.x与y具有较强的线性相关关系
C.x与y几乎不具有线性相关关系
D.x与y的线性相关关系还需进一步确定
15.据两个变量x,y之间的观测数据画成散点图如图,这两个变量是否具有线性相关关系 (答是或否).
16.对相关系数r,
①r越大,线性相关程度越大;②r越小,线性相关程度越大;③|r|越大,线性相关程度越小,|r|越接近0,线性相关程度越大;④|r|≤1且|r|越接近1,线性相关程度越大,|r|越接近0,线性相关程度越小.
以上说法中,正确说法的序号是 .
17.对四组试验进行相关性检验,分别选择不同的模型,它们的相关系数r如下,其中拟合效果最好的模型是 .(填序号)
①模型Ⅰ的相关系数r为-0.98;②模型Ⅱ的相关系数r为0.80;③模型Ⅲ的相关系数r为-0.50;
④模型Ⅳ的相关系数r为0.25.
18.某农场经过观测得到水稻产量和施化肥量的统计数据如表:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
求水稻产量与施化肥量的相关系数,并判断相关性的强弱.
相关系数公式:r==
参考数据:=7 000,=1 132 725,xiyi=87 175.
19.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取次数 1 2 3 4 5 6 7 8
医疗物资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次数 9 10 11 12 13 14 15 16
医疗物资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=.
【参考答案】
1.BC 解析:A中两个变量为函数关系,不是线性相关关系,所以A错误;B中两个变量有明显的正相关,所以具有线性相关性,所以B正确;C中两个变量有明显的负相关,所以具有线性相关性,所以C正确;D中两个变量不具有相关性,所以D错误.
2.C解析:根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;故r1>0,r3>0;r2<0,r4<0;又(1)与(2)中散点图更接近于一条直线,故r1>r3,r2
4.C解析:由表中数据可知:y随x的减小而增大,是负相关关系.
5.D解析:有相关性可知从左到右的第一个图是正相关,第二个图相关性不明确,所以不相关,第三个图是负相关.
6.C解析:月收入的中位数是=16,收入增加,支出增加,故x与y有正线性相关关系.
7. ②④解析:对于①,正方形的边长a和面积S是函数关系,不是相关关系;对于②,一般情况下,一个人的身高h和右手一拃长x是正相关关系;对于③,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系;对于④,一般情况下,一个人的身高h和他的体重x是正相关关系.
8. C解析:仔细观察点A,B,C,D(7,10),E,可知点ABDE在一条直线附近,而C点明显偏离此直线,由此可知去掉点C后,使剩下的四点组成的数组相关系数最大.
9. 解:画出散点图如图所示,由图可知x,Y有线性关系.
=5,=47.5,=120,=9 900,xiyi=1 080,r=
=≈0.982 7.
故x与Y之间具有很强的正相关关系.
10.C 解析:由线性相关系数r1=0.785 9>0知x与y正相关,由线性相关系数r2=-0.956 8<0知u,v负相关,又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强.
11.D解析:由这两个散点图可以判断,变量x与y为负相关,y与z为正相关,所以x与z为负相关.
12.D解析:对于①,一般情况下,某商品的销售价格与销售量是负相关关系;
对于②,学生的学籍号与学生的数学成绩没有相关关系;
对于③,一般情况下,坚持每天吃早餐的人数与患胃病的人数是负相关关系;
对于④,一般情况下,气温与冷饮销售量是正相关关系;
对于⑤,一般情况下,电瓶车的质量和行驶每千米的耗电量是正相关关系.
13.BD解析:A选项1月到9月中,最高气温与最低气温相差最大的是1月,错误;
B选项1月到9月的最高气温与月份具有比较好的线性相关关系,正确;
C选项最高气温与最低气温的差不稳定,错误;
D选项最低气温与最高气温间存在较好的正相关关系,正确.
14.B解析:x与y为负相关,非常接近1,所以相关性很强.
15. 否 解析:由散点图可知,散点图分布无任何规律,不在一条直线附近,所以,这两个变量没有线性相关关系.
16. ④ 解析:两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强;r的绝对值非常接近于0时,表示两个变量之间几乎不存在线性相关性.
17.①解析:相关系数的正负表明两个变量是正相关还是负相关,相关系数大于零正相关,小于零负相关,相关系数的绝对值越大,相关性越强.故①的拟合效果最好.
18. 解:==30,==,
故r==≈≈0.97,故具有很强的相关性.
19.解:(1)由样本数据得(x,i)(i=1,2,3,…,16)的相关系数为
r==≈-0.18;
由于|r|<0.25,因此可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小.
(2)由于=9.97,s≈0.212,由样本数据可以看出抽取的第13个零件的尺寸在(-3s,+3s)以外,因此需对当天的生产过程进行检查.
