高二数学人教A版2019选择性必修第三册 7.2 离散型随机变量及其分布列(分层练习)(含解析)
文档属性
| 名称 | 高二数学人教A版2019选择性必修第三册 7.2 离散型随机变量及其分布列(分层练习)(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-24 08:56:09 | ||
图片预览


文档简介
7.2 离散型随机变量及其分布列
基 础 练
巩固新知 夯实基础
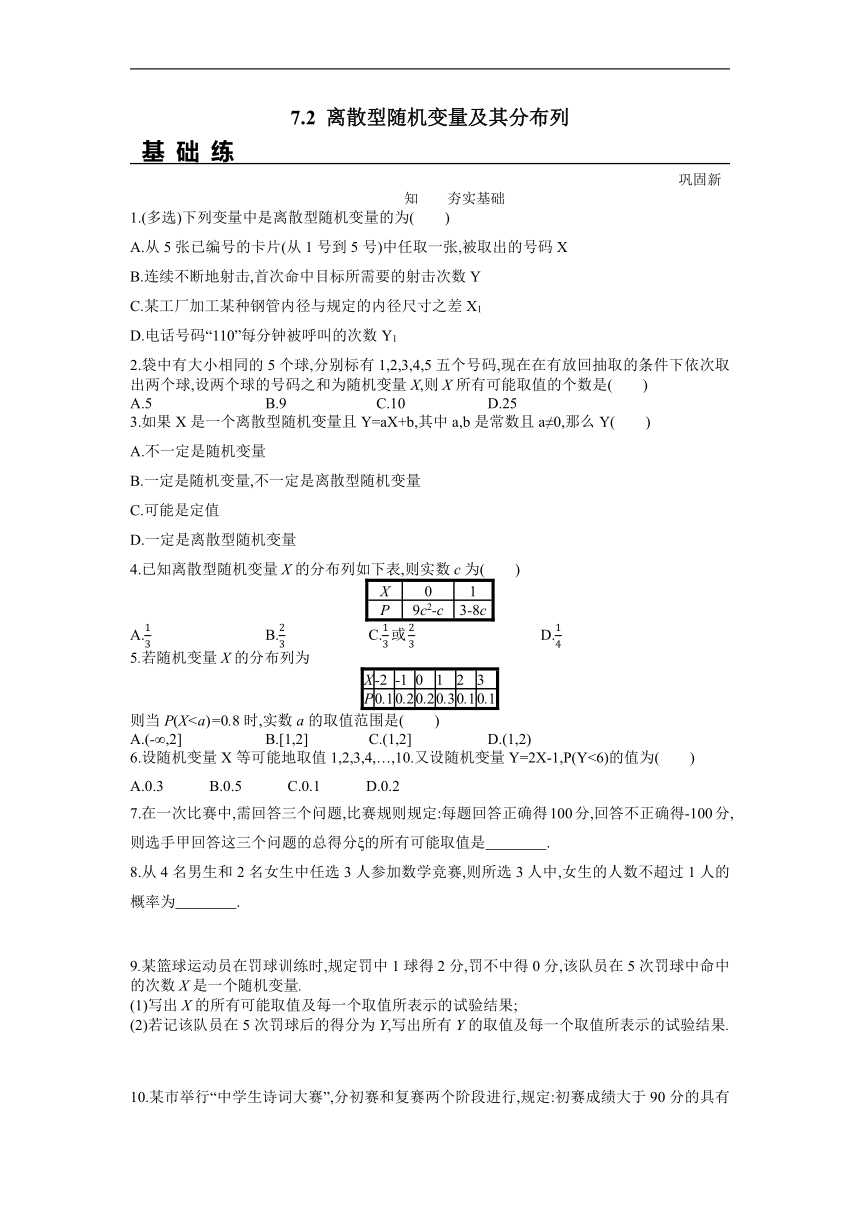
1.(多选)下列变量中是离散型随机变量的为( )
A.从5张已编号的卡片(从1号到5号)中任取一张,被取出的号码X
B.连续不断地射击,首次命中目标所需要的射击次数Y
C.某工厂加工某种钢管内径与规定的内径尺寸之差X1
D.电话号码“110”每分钟被呼叫的次数Y1
2.袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球的号码之和为随机变量X,则X所有可能取值的个数是( )
A.5 B.9 C.10 D.25
3.如果X是一个离散型随机变量且Y=aX+b,其中a,b是常数且a≠0,那么Y( )
A.不一定是随机变量
B.一定是随机变量,不一定是离散型随机变量
C.可能是定值
D.一定是离散型随机变量
4.已知离散型随机变量X的分布列如下表,则实数c为( )
X 0 1
P 9c2-c 3-8c
A. B. C. D.
5.若随机变量X的分布列为
X -2 -1 0 1 2 3
P 0.1 0.2 0.2 0.3 0.1 0.1
则当P(XA.(-∞,2] B.[1,2] C.(1,2] D.(1,2)
6.设随机变量X等可能地取值1,2,3,4,…,10.又设随机变量Y=2X-1,P(Y<6)的值为( )
A.0.3 B.0.5 C.0.1 D.0.2
7.在一次比赛中,需回答三个问题,比赛规则规定:每题回答正确得100分,回答不正确得-100分,则选手甲回答这三个问题的总得分ξ的所有可能取值是 .
8.从4名男生和2名女生中任选3人参加数学竞赛,则所选3人中,女生的人数不超过1人的概率为 .
9.某篮球运动员在罚球训练时,规定罚中1球得2分,罚不中得0分,该队员在5次罚球中命中的次数X是一个随机变量.
(1)写出X的所有可能取值及每一个取值所表示的试验结果;
(2)若记该队员在5次罚球后的得分为Y,写出所有Y的取值及每一个取值所表示的试验结果.
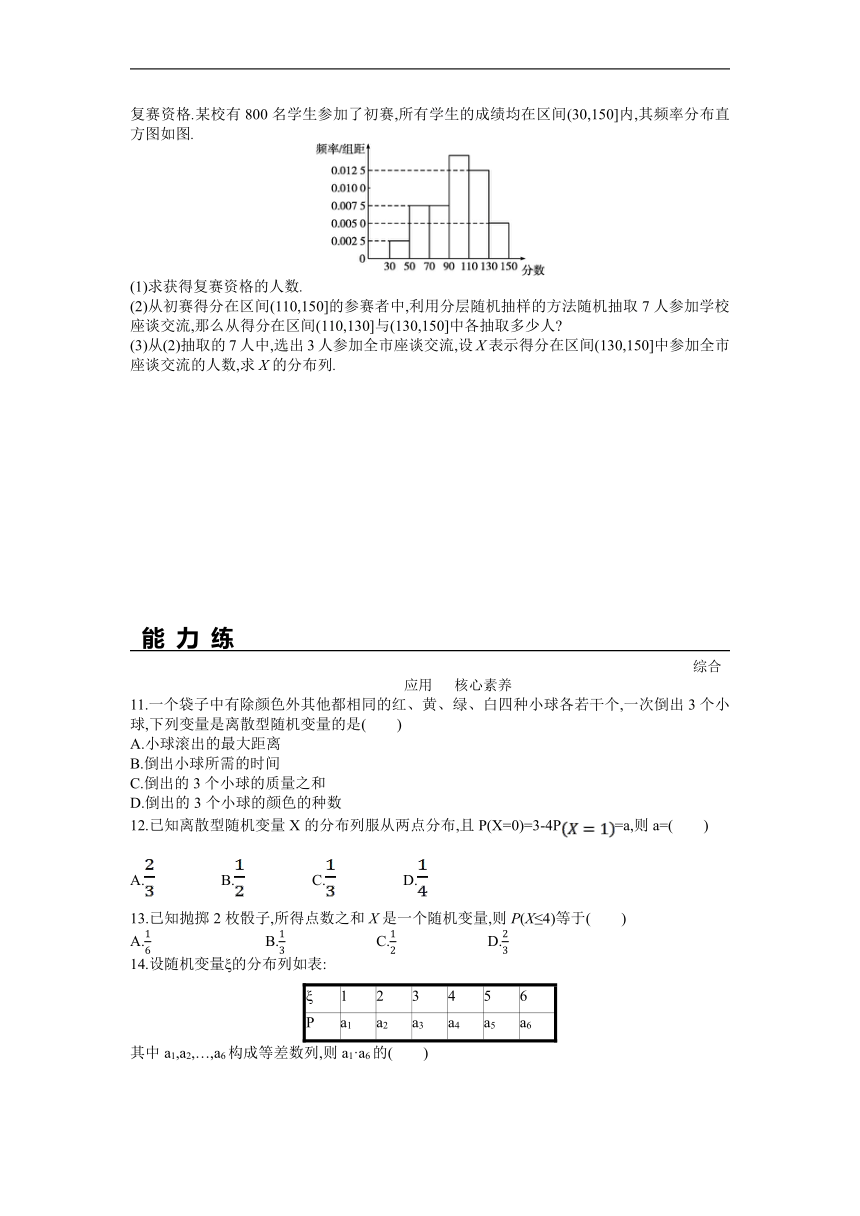
10.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(1)求获得复赛资格的人数.
(2)从初赛得分在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]中各抽取多少人
(3)从(2)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列.
能 力 练
综合应用 核心素养
11.一个袋子中有除颜色外其他都相同的红、黄、绿、白四种小球各若干个,一次倒出3个小球,下列变量是离散型随机变量的是( )
A.小球滚出的最大距离
B.倒出小球所需的时间
C.倒出的3个小球的质量之和
D.倒出的3个小球的颜色的种数
12.已知离散型随机变量X的分布列服从两点分布,且P(X=0)=3-4P=a,则a=( )
A. B. C. D.
13.已知抛掷2枚骰子,所得点数之和X是一个随机变量,则P(X≤4)等于( )
A. B. C. D.
14.设随机变量ξ的分布列如表:
ξ 1 2 3 4 5 6
P a1 a2 a3 a4 a5 a6
其中a1,a2,…,a6构成等差数列,则a1·a6的( )
A.最大值为 B.最大值为 C.最小值为 D.最小值为
15.甲、乙两队在一次对抗赛的某一轮中有3个抢答题,比赛规定:对于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分);若X是甲队在该轮比赛获胜时的得分(分数高者胜),则X的所有可能取值是 .
16.袋中有4个红球、3个黑球,从袋中任取4个球,取到1个红球得1分,取到1个黑球得3分,记得分为随机变量ξ,则P(ξ≤6)= .
17.设随机变量X的概率分布列如表,则P(|x-2|=1)=________.
X 1 2 3 4
P m
18.甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为,乙每次投篮命中的概率为,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数X的分布列.
19.唐代饼茶的制作一直延续至今,它的制作由“炙”“碾”“罗”三道工序组成.根据分析,甲、乙、丙三位学徒能通过“炙”这道工序的概率分别是0.5,0.6,0.5;能通过“碾”这道工序的概率分别是0.8,0.5,0.4;由于他们平时学习刻苦,都能通过“罗”这道工序.若这三道工序之间通过与否没有影响.
(1)求甲、乙、丙三位学徒中恰好有一人通过“炙”这道工序的概率;
(2)设只要通过三道工序就可以制成饼茶,求甲、乙、丙三位学徒中制成饼茶人数X的分布列.
【参考答案】
1.ABD 解析:从5张已编号的卡片(从1号到5号)中任取一张,被取出的号码X的可能取值为1,2,3,4,5,故A是离散型随机变量;连续不断地射击,首次命中目标所需要的射击次数Y的可能取值为1,2,3,4,5,…,故B是离散型随机变量;某工厂加工某种钢管内径与规定的内径尺寸之差X1,其取值不能一一列举出来,故C不是离散型随机变量;电话号码“110”每分钟被呼叫的次数Y1的可能取值为0,1,2,3,4,5…,故D是离散型随机变量.
2. B 解析:X的可能取值是2,3,4,5,6,7,8,9,10,共9个.
3.D 解析:由于X是离散型随机变量,因此Y=aX+b也是离散型随机变量.
4.A 解析:由离散型随机变量分布列的性质知,9c2-c≥0,3-8c≥0,9c2-c+3-8c=1,解得c=.故选A.
5.C 解析:由随机变量X的分布列知P(X<1)=0.5,P(X<2)=0.8,故当P(X6.A 解析:Y<6,即2X-1<6,所以X<3.5.X=1,2,3,P=0.3.
7. 300,100,-100,-300解析:可能回答全对,两对一错,两错一对,全错四种结果,相应得分为300分,100分,-100分,-300分.
8. 解析:设所选女生人数为随机变量X,则P(X≤1)=P(X=0)+P(X=1)=+=.
9.解:(1)X的所有可能取值为0,1,2,3,4,5.它们表示在5次罚球中分别罚中0次,1次,2次,3次,4次,5次.
(2)Y的所有可能取值为0,2,4,6,8,10.它们表示5次罚球后分别得0分,2分,4分,6分,8分,10分.
10.解:(1)由题意知在区间(90,110]的频率为1-20×(0.0025+0.005+0.0075×2+0.0125)=0.3,
0.3+(0.0125+0.005)×20=0.65,故获得复赛资格的人数为800×0.65=520.
(2)0.0125∶0.005=5∶2,在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人,则在区间(110,130]与(130,150]中各抽取5人,2人.
(3)X的可能取值为0,1,2,则P(X=0)=,P(X=1)=,P(X=2)=.
故X的分布列为
X 0 1 2
P
11.D 解析:对于A,小球滚出的最大距离不是离散型随机变量,因为滚出的最大距离不能一一列出;对于B,倒出小球所需的时间不是离散型随机变量,因为所需的时间不能一一列出;对于C,3个小球的质量之和是一个定值,不是随机变量;对于D,倒出的3个小球的颜色的种数可以一一列出,是离散型随机变量.
12.C 解析:因为X的分布列服从两点分布,所以P+P=1,
因为P=3-4P=a,所以P=3-4[1-P],所以P=,即a=.
13.A 解析:根据题意,P(X=2)=,P(X=3)=,P(X=4)=,故P(X≤4)=.
14.B 解析:a1+a2+a3+a4+a5+a6=1,由等差数列的性质可得a1+a6=,所以a1·a6≤=,
所以a1·a6的最大值为,无最小值.
15.-1,0,1,2,3 解析:X=-1,甲抢到一题但答错了,而乙抢到了两个题目都答错了,
X=0,甲没抢到题,乙抢到题目答错至少2个题或甲抢到2题,但答时一对一错,而乙答错一个题目,
X=1,甲抢到1题且答对或甲抢到3题,且1错2对,X=2,甲抢到2题均答对,X=3,甲抢到3题均答对.
16. 解析:取出的4个球中红球的个数可能为4,3,2,1,相应的黑球的个数为0,1,2,3,其得分ξ=4,6,8,10,则P(ξ≤6)=P(ξ=4)+P(ξ=6)=.
17. 解析:由|x-2|=1,解得x=1,3,所以P(|x-2|=1)=P(X=1或3)=+=.
18.解:(1)由题意甲获胜的概率:P=+××+××××=.
(2)由题意知,投篮结束时甲的投篮次数X的可能取值为1,2,3,P(X=1)=+×=,
P(X=2)=××+×××=,
P(X=3)=××××+×××××+×××××=,
所以X的分布列为:
X 1 2 3
P
19.解:(1)设A,B,C分别表示事件“甲、乙、丙通过‘炙’这道工序”,则所求概率
P=P+P+P=0.5×(1-0.6)×(1-0.5)+(1-0.5)×0.6×(1-0.5)+(1-0.5)×(1-0.6)×0.5=0.35.
(2)甲制成饼茶的概率为P甲=0.5×0.8=0.4,同理P乙=0.6×0.5=0.3,P丙=0.5×0.4=0.2.
随机变量X的可能取值为0,1,2,3,
P=××=0.336,P=0.4××+××0.2+×0.3×=0.452,P=0.4×0.3×(1-0.2)+0.4××0.2+×0.3×0.2=0.188,P=0.4×0.3×0.2=0.024.
故X的分布列为
X 0 1 2 3
P 0.336 0.452 0.188 0.024
基 础 练
巩固新知 夯实基础
1.(多选)下列变量中是离散型随机变量的为( )
A.从5张已编号的卡片(从1号到5号)中任取一张,被取出的号码X
B.连续不断地射击,首次命中目标所需要的射击次数Y
C.某工厂加工某种钢管内径与规定的内径尺寸之差X1
D.电话号码“110”每分钟被呼叫的次数Y1
2.袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球的号码之和为随机变量X,则X所有可能取值的个数是( )
A.5 B.9 C.10 D.25
3.如果X是一个离散型随机变量且Y=aX+b,其中a,b是常数且a≠0,那么Y( )
A.不一定是随机变量
B.一定是随机变量,不一定是离散型随机变量
C.可能是定值
D.一定是离散型随机变量
4.已知离散型随机变量X的分布列如下表,则实数c为( )
X 0 1
P 9c2-c 3-8c
A. B. C. D.
5.若随机变量X的分布列为
X -2 -1 0 1 2 3
P 0.1 0.2 0.2 0.3 0.1 0.1
则当P(X
6.设随机变量X等可能地取值1,2,3,4,…,10.又设随机变量Y=2X-1,P(Y<6)的值为( )
A.0.3 B.0.5 C.0.1 D.0.2
7.在一次比赛中,需回答三个问题,比赛规则规定:每题回答正确得100分,回答不正确得-100分,则选手甲回答这三个问题的总得分ξ的所有可能取值是 .
8.从4名男生和2名女生中任选3人参加数学竞赛,则所选3人中,女生的人数不超过1人的概率为 .
9.某篮球运动员在罚球训练时,规定罚中1球得2分,罚不中得0分,该队员在5次罚球中命中的次数X是一个随机变量.
(1)写出X的所有可能取值及每一个取值所表示的试验结果;
(2)若记该队员在5次罚球后的得分为Y,写出所有Y的取值及每一个取值所表示的试验结果.
10.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(1)求获得复赛资格的人数.
(2)从初赛得分在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]中各抽取多少人
(3)从(2)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列.
能 力 练
综合应用 核心素养
11.一个袋子中有除颜色外其他都相同的红、黄、绿、白四种小球各若干个,一次倒出3个小球,下列变量是离散型随机变量的是( )
A.小球滚出的最大距离
B.倒出小球所需的时间
C.倒出的3个小球的质量之和
D.倒出的3个小球的颜色的种数
12.已知离散型随机变量X的分布列服从两点分布,且P(X=0)=3-4P=a,则a=( )
A. B. C. D.
13.已知抛掷2枚骰子,所得点数之和X是一个随机变量,则P(X≤4)等于( )
A. B. C. D.
14.设随机变量ξ的分布列如表:
ξ 1 2 3 4 5 6
P a1 a2 a3 a4 a5 a6
其中a1,a2,…,a6构成等差数列,则a1·a6的( )
A.最大值为 B.最大值为 C.最小值为 D.最小值为
15.甲、乙两队在一次对抗赛的某一轮中有3个抢答题,比赛规定:对于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分);若X是甲队在该轮比赛获胜时的得分(分数高者胜),则X的所有可能取值是 .
16.袋中有4个红球、3个黑球,从袋中任取4个球,取到1个红球得1分,取到1个黑球得3分,记得分为随机变量ξ,则P(ξ≤6)= .
17.设随机变量X的概率分布列如表,则P(|x-2|=1)=________.
X 1 2 3 4
P m
18.甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为,乙每次投篮命中的概率为,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数X的分布列.
19.唐代饼茶的制作一直延续至今,它的制作由“炙”“碾”“罗”三道工序组成.根据分析,甲、乙、丙三位学徒能通过“炙”这道工序的概率分别是0.5,0.6,0.5;能通过“碾”这道工序的概率分别是0.8,0.5,0.4;由于他们平时学习刻苦,都能通过“罗”这道工序.若这三道工序之间通过与否没有影响.
(1)求甲、乙、丙三位学徒中恰好有一人通过“炙”这道工序的概率;
(2)设只要通过三道工序就可以制成饼茶,求甲、乙、丙三位学徒中制成饼茶人数X的分布列.
【参考答案】
1.ABD 解析:从5张已编号的卡片(从1号到5号)中任取一张,被取出的号码X的可能取值为1,2,3,4,5,故A是离散型随机变量;连续不断地射击,首次命中目标所需要的射击次数Y的可能取值为1,2,3,4,5,…,故B是离散型随机变量;某工厂加工某种钢管内径与规定的内径尺寸之差X1,其取值不能一一列举出来,故C不是离散型随机变量;电话号码“110”每分钟被呼叫的次数Y1的可能取值为0,1,2,3,4,5…,故D是离散型随机变量.
2. B 解析:X的可能取值是2,3,4,5,6,7,8,9,10,共9个.
3.D 解析:由于X是离散型随机变量,因此Y=aX+b也是离散型随机变量.
4.A 解析:由离散型随机变量分布列的性质知,9c2-c≥0,3-8c≥0,9c2-c+3-8c=1,解得c=.故选A.
5.C 解析:由随机变量X的分布列知P(X<1)=0.5,P(X<2)=0.8,故当P(X
7. 300,100,-100,-300解析:可能回答全对,两对一错,两错一对,全错四种结果,相应得分为300分,100分,-100分,-300分.
8. 解析:设所选女生人数为随机变量X,则P(X≤1)=P(X=0)+P(X=1)=+=.
9.解:(1)X的所有可能取值为0,1,2,3,4,5.它们表示在5次罚球中分别罚中0次,1次,2次,3次,4次,5次.
(2)Y的所有可能取值为0,2,4,6,8,10.它们表示5次罚球后分别得0分,2分,4分,6分,8分,10分.
10.解:(1)由题意知在区间(90,110]的频率为1-20×(0.0025+0.005+0.0075×2+0.0125)=0.3,
0.3+(0.0125+0.005)×20=0.65,故获得复赛资格的人数为800×0.65=520.
(2)0.0125∶0.005=5∶2,在区间(110,150]的参赛者中,利用分层随机抽样的方法随机抽取7人,则在区间(110,130]与(130,150]中各抽取5人,2人.
(3)X的可能取值为0,1,2,则P(X=0)=,P(X=1)=,P(X=2)=.
故X的分布列为
X 0 1 2
P
11.D 解析:对于A,小球滚出的最大距离不是离散型随机变量,因为滚出的最大距离不能一一列出;对于B,倒出小球所需的时间不是离散型随机变量,因为所需的时间不能一一列出;对于C,3个小球的质量之和是一个定值,不是随机变量;对于D,倒出的3个小球的颜色的种数可以一一列出,是离散型随机变量.
12.C 解析:因为X的分布列服从两点分布,所以P+P=1,
因为P=3-4P=a,所以P=3-4[1-P],所以P=,即a=.
13.A 解析:根据题意,P(X=2)=,P(X=3)=,P(X=4)=,故P(X≤4)=.
14.B 解析:a1+a2+a3+a4+a5+a6=1,由等差数列的性质可得a1+a6=,所以a1·a6≤=,
所以a1·a6的最大值为,无最小值.
15.-1,0,1,2,3 解析:X=-1,甲抢到一题但答错了,而乙抢到了两个题目都答错了,
X=0,甲没抢到题,乙抢到题目答错至少2个题或甲抢到2题,但答时一对一错,而乙答错一个题目,
X=1,甲抢到1题且答对或甲抢到3题,且1错2对,X=2,甲抢到2题均答对,X=3,甲抢到3题均答对.
16. 解析:取出的4个球中红球的个数可能为4,3,2,1,相应的黑球的个数为0,1,2,3,其得分ξ=4,6,8,10,则P(ξ≤6)=P(ξ=4)+P(ξ=6)=.
17. 解析:由|x-2|=1,解得x=1,3,所以P(|x-2|=1)=P(X=1或3)=+=.
18.解:(1)由题意甲获胜的概率:P=+××+××××=.
(2)由题意知,投篮结束时甲的投篮次数X的可能取值为1,2,3,P(X=1)=+×=,
P(X=2)=××+×××=,
P(X=3)=××××+×××××+×××××=,
所以X的分布列为:
X 1 2 3
P
19.解:(1)设A,B,C分别表示事件“甲、乙、丙通过‘炙’这道工序”,则所求概率
P=P+P+P=0.5×(1-0.6)×(1-0.5)+(1-0.5)×0.6×(1-0.5)+(1-0.5)×(1-0.6)×0.5=0.35.
(2)甲制成饼茶的概率为P甲=0.5×0.8=0.4,同理P乙=0.6×0.5=0.3,P丙=0.5×0.4=0.2.
随机变量X的可能取值为0,1,2,3,
P=××=0.336,P=0.4××+××0.2+×0.3×=0.452,P=0.4×0.3×(1-0.2)+0.4××0.2+×0.3×0.2=0.188,P=0.4×0.3×0.2=0.024.
故X的分布列为
X 0 1 2 3
P 0.336 0.452 0.188 0.024
