小学数学苏教版六年级下比的应用 课件(共35张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下比的应用 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 158.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-24 16:11:22 | ||
图片预览











文档简介
(共35张PPT)
生活中的比
----比的应用
义务教育小学数学六年级上册
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
阅读与理解:
48厘米是这个三角形的什么?
三角形有三条边,知道了其中两条边的长度比是5:2,我们能想到第三条边的长度份数吗?
周长
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
三条边的长度比是5:5:2
或者是5:2:2
三角形边的关系:任意两边之和大于第三条边。
√
×
分析:
等腰三角形:两条相等的腰,一条底。
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
解答:
5+5+2=12
答:这个等腰三角形的三条边的长度分别是20厘米、20厘米和8厘米。
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
回顾与反思:
应用比解决三角形中边的长度问题要注意什么?
满足三角形边的关系的规定:任意两边之和大于第三条边。
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
阅读与理解:
这面墙可以充当长方形的什么?
56米长的篱笆是长方形的几条边的长度之和?
长或宽
三条边
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
分析:
要求这个长方形菜地的面积,我们一般情况下也还是要先求出这个长方形菜地的长和宽。题目中的56米长的篱笆不是长方形的周长了,因为小华借助了一面墙,那么这面墙既可以充当长,也可以充当宽,我们可以用图来表示:
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
分析:
3
2
2
3
3
2
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3
2
2
3+2+2=7
56÷7=8(米 )
8×3=24(米 )
8×2=16(米 )
24×16=384(平方米)
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3
3
2
3+3+2=8
56÷8=7(米)
7×3=21(米)
7×2=14(米)
21×14=294(平方米)
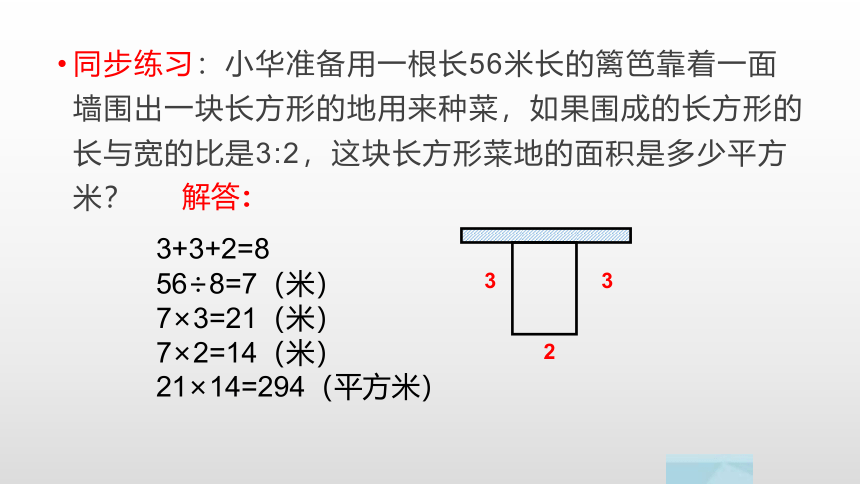
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3+3+2=8
56÷8=7(米)
7×3=21(米)
7×2=14(米)
21×14=294(平方米)
3+2+2=7
56÷7=8(米)
8×3=24(米)
8×2=16(米)
24×16=384(平方米)
答:这块长方形菜地的面积可能是384平方米,也可能是294平方米。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
阅读与理解:
知道了甲、乙两种糖的单价比4:5和质量比4:1,我们可以求出总价比16:5。
知道了什锦糖的数量100千克和单价8.4元,可以求出什锦糖的总价是840元。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
分析:
把什锦糖的总价按照两种糖的总价比进行按比例分配。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
解答:
(4×4):(5×1)= 16:5
100×8.4= 840(元)
答:甲种糖是640元 乙种糖是200元。
840- 640 = 200(元)
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
阅读与理解:
原有的锌和铜一共是84千克,但是熔铸成合金的总量不是84千克,而是96千克。
原有的铜不够锌的2倍。
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
分析:
把合金总量96千克按照1:2的比进行分配,分别求出锌和铜的量,然后把合金中铜的量减去12千克就是原有铜的千克数。
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
解答:
84+12=96(千克 ) 合金总量
96÷(1+2)=32(千克) 合金中锌的量
32×2=64(千克 ) 合金中铜的量
64-12=52(千克 ) 原有铜的量
答:原有铜52千克。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
阅读与理解:
三种建筑材料都是30吨,但是要把这三种建筑材料按照3:2:5这个比进行混合,也就是在混凝土中沙子比水泥要多一些,沙子要比石子又少一些。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
分析:
题目中三种材料的质量都是30吨,沙子正好用完,说明30吨和3份正好是对应的。这样就可以求出一份,再求出水泥的2份对应的量以及石子的5份对应的量,然后分别和30吨进行比较。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
解答:
30÷3=10(吨)
10×2=20(吨) 30-20=10(吨)
10×5=50(吨) 50-30=20(吨)
答:水泥还会剩10吨,石子还要增加20吨。
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
阅读与理解
有三个车间一共105人。
第二车间出现了两次,但是两次的份数不一样。
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
分析:
第一车间的:第二车间的=2:3
第二车间的:第三车间的=4:5
=8:12
=12:15
第一车间的:第二车间的:第三车间的 = 8:12:15
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
解答:
2:3=8:12
4:5=12:15
8+12+15=35
105÷35=3(人)
3×8=24(人)
3×12=36(人)
3×15=45(人)
答:第一车间有24人,第二车间有36人,第三车间有45人。
同步练习:六年级1班学生三天共植树150棵,第一天与第二天植树的棵数比是5:6,第二天与第三天植树的棵数比是3:2。第一、二、三天各植树多少棵?
第一天的:第二天的:第三天的 = 5 : 6 : 4
=6:4
5 + 6 + 4 =15
150÷15 =10(棵)
10×5 =50(棵)
10×6 =60(棵)
10×4 =40(棵)
答:第一天植树50棵,第二天植树60棵,第三天植树 40棵。
例4:货车与客车的速度比是3:5,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
阅读与理解:
货车与客车是同时出发的,
货车与客车的速度比是3:5,
货车与客车的路程比是( ):( )
3 5
例4:货车与客车的速度比是3:5,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
分析:
甲
乙
货车
客车
中点
6KM
(3+5)÷2=4
4-3=1
6÷1=6(千米)
6×(3+5)=48(千米)
答:甲、乙两站相距48千米。
解答:
同步练习:货车与客车的速度比是3:7,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
分析与解答:
甲
乙
货车
客车
中点
6KM
(3+7)÷2=5
5-3=2
6÷2=3(千米)
3×(3+7)=30(千米)
答:甲、乙两站相距30千米。
练习1:一个等腰三角形的其中两个内角的度数比是2:1,这个三角形三个内角分别是多少度?
2+2+1=5
180÷5=36°
36×2=72°
答:这三个内角分别是72°,72°和36°。
2+1+1=4
180÷4=45°
45×2=90°
答:这三个内角分别是45°,45°和90°。
巩固练习
练习2: 小华准备用一根长60米的篱笆围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
60÷2=30(米)
长与宽的和
长
宽
面积
答:这块长方形菜地的面积是216平方米。
18×12=216(平方米)
练习2: 小华准备用一根长60米的篱笆围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
回顾与反思:
回顾刚才解决这个问题的过程,想一想,要注意什么?
解答这个问题的时候,我们要注意分清题目中的数量与所给的比的份数之间是否存在对应关系,然后可以转化为分数乘法问题,当然也可以用先求一份数、再求几份数的方法进行解答。
练习3:有三批货物一共值152万元,第一、二、三批货物的质量比是2:4:3,单价的比是6:5:2。第二批货物值多少万元?
(2×6):(4×5):(3×2)
=12:20:6
12+20+6=38
152÷38=4( 万元 )
20×4=80( 万元 )
答:第二批货物值80万元。
巩固练习
练习4:两根同样长的铁条,一根按3:4:5的比锯成三段,另一根按7:9:11的比锯成三段,锯成的铁条有几种不同的长度?
答:有五种不同的长度。
练习5:货车与客车的速度比是4:5,两车同时从甲、乙两站相向行驶,在离中点80千米处相遇。甲、乙两站相距多少千米?
4+5=9
9÷2=4.5
4.5-4=0.5
80÷0.5=160(千米)
160×(4+5)
=160×9
=1440(千米)
答:甲、乙两站相距1440千米。
巩固练习
回顾与总结
应用比解决问题的方法:
一种是用整数法先求一份数,再求出相应的几份数。
另一种是用分数法先求各部分占总数的几分之几,再求各部分数。
解决问题的策略:画图、转化
谢谢!
生活中的比
----比的应用
义务教育小学数学六年级上册
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
阅读与理解:
48厘米是这个三角形的什么?
三角形有三条边,知道了其中两条边的长度比是5:2,我们能想到第三条边的长度份数吗?
周长
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
三条边的长度比是5:5:2
或者是5:2:2
三角形边的关系:任意两边之和大于第三条边。
√
×
分析:
等腰三角形:两条相等的腰,一条底。
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
解答:
5+5+2=12
答:这个等腰三角形的三条边的长度分别是20厘米、20厘米和8厘米。
例1:用一根48厘米长的铁丝围成一个等腰三角形,其中两条边的长度比是5:2,这个三角形的三条边的长度分别是多少厘米?
回顾与反思:
应用比解决三角形中边的长度问题要注意什么?
满足三角形边的关系的规定:任意两边之和大于第三条边。
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
阅读与理解:
这面墙可以充当长方形的什么?
56米长的篱笆是长方形的几条边的长度之和?
长或宽
三条边
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
分析:
要求这个长方形菜地的面积,我们一般情况下也还是要先求出这个长方形菜地的长和宽。题目中的56米长的篱笆不是长方形的周长了,因为小华借助了一面墙,那么这面墙既可以充当长,也可以充当宽,我们可以用图来表示:
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
分析:
3
2
2
3
3
2
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3
2
2
3+2+2=7
56÷7=8(米 )
8×3=24(米 )
8×2=16(米 )
24×16=384(平方米)
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3
3
2
3+3+2=8
56÷8=7(米)
7×3=21(米)
7×2=14(米)
21×14=294(平方米)
同步练习:小华准备用一根长56米长的篱笆靠着一面墙围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
解答:
3+3+2=8
56÷8=7(米)
7×3=21(米)
7×2=14(米)
21×14=294(平方米)
3+2+2=7
56÷7=8(米)
8×3=24(米)
8×2=16(米)
24×16=384(平方米)
答:这块长方形菜地的面积可能是384平方米,也可能是294平方米。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
阅读与理解:
知道了甲、乙两种糖的单价比4:5和质量比4:1,我们可以求出总价比16:5。
知道了什锦糖的数量100千克和单价8.4元,可以求出什锦糖的总价是840元。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
分析:
把什锦糖的总价按照两种糖的总价比进行按比例分配。
例2:甲、乙两种糖的单价比是4:5,质量比是4:1,把这两种糖混合成100千克的什锦糖,单价为8.4元。原来每种糖的总钱数各是多少元?
解答:
(4×4):(5×1)= 16:5
100×8.4= 840(元)
答:甲种糖是640元 乙种糖是200元。
840- 640 = 200(元)
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
阅读与理解:
原有的锌和铜一共是84千克,但是熔铸成合金的总量不是84千克,而是96千克。
原有的铜不够锌的2倍。
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
分析:
把合金总量96千克按照1:2的比进行分配,分别求出锌和铜的量,然后把合金中铜的量减去12千克就是原有铜的千克数。
同步练习1:某车间原有锌和铜共84千克,现在要把锌和铜按1:2的比熔铸成一种合金,需要添加12千克铜。原有铜多少千克?
解答:
84+12=96(千克 ) 合金总量
96÷(1+2)=32(千克) 合金中锌的量
32×2=64(千克 ) 合金中铜的量
64-12=52(千克 ) 原有铜的量
答:原有铜52千克。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
阅读与理解:
三种建筑材料都是30吨,但是要把这三种建筑材料按照3:2:5这个比进行混合,也就是在混凝土中沙子比水泥要多一些,沙子要比石子又少一些。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
分析:
题目中三种材料的质量都是30吨,沙子正好用完,说明30吨和3份正好是对应的。这样就可以求出一份,再求出水泥的2份对应的量以及石子的5份对应的量,然后分别和30吨进行比较。
同步练习2:一种混凝土是用沙子、水泥、石子按照3:2:5的比混合而成的,现在这三种材料各有30吨。如果沙子正好用完,水泥还会剩多少吨?石子还要增加多少吨?
解答:
30÷3=10(吨)
10×2=20(吨) 30-20=10(吨)
10×5=50(吨) 50-30=20(吨)
答:水泥还会剩10吨,石子还要增加20吨。
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
阅读与理解
有三个车间一共105人。
第二车间出现了两次,但是两次的份数不一样。
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
分析:
第一车间的:第二车间的=2:3
第二车间的:第三车间的=4:5
=8:12
=12:15
第一车间的:第二车间的:第三车间的 = 8:12:15
例3:一个工厂有三个车间共105人,第一车间与第二车间人数的比是2:3,第二车间与第三车间人数的比是4:5,这三个车间分别有多少人?
解答:
2:3=8:12
4:5=12:15
8+12+15=35
105÷35=3(人)
3×8=24(人)
3×12=36(人)
3×15=45(人)
答:第一车间有24人,第二车间有36人,第三车间有45人。
同步练习:六年级1班学生三天共植树150棵,第一天与第二天植树的棵数比是5:6,第二天与第三天植树的棵数比是3:2。第一、二、三天各植树多少棵?
第一天的:第二天的:第三天的 = 5 : 6 : 4
=6:4
5 + 6 + 4 =15
150÷15 =10(棵)
10×5 =50(棵)
10×6 =60(棵)
10×4 =40(棵)
答:第一天植树50棵,第二天植树60棵,第三天植树 40棵。
例4:货车与客车的速度比是3:5,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
阅读与理解:
货车与客车是同时出发的,
货车与客车的速度比是3:5,
货车与客车的路程比是( ):( )
3 5
例4:货车与客车的速度比是3:5,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
分析:
甲
乙
货车
客车
中点
6KM
(3+5)÷2=4
4-3=1
6÷1=6(千米)
6×(3+5)=48(千米)
答:甲、乙两站相距48千米。
解答:
同步练习:货车与客车的速度比是3:7,两车同时从甲、乙两站出发相向行驶,在离中点6千米处相遇。甲、乙两站相距多少千米?
分析与解答:
甲
乙
货车
客车
中点
6KM
(3+7)÷2=5
5-3=2
6÷2=3(千米)
3×(3+7)=30(千米)
答:甲、乙两站相距30千米。
练习1:一个等腰三角形的其中两个内角的度数比是2:1,这个三角形三个内角分别是多少度?
2+2+1=5
180÷5=36°
36×2=72°
答:这三个内角分别是72°,72°和36°。
2+1+1=4
180÷4=45°
45×2=90°
答:这三个内角分别是45°,45°和90°。
巩固练习
练习2: 小华准备用一根长60米的篱笆围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
60÷2=30(米)
长与宽的和
长
宽
面积
答:这块长方形菜地的面积是216平方米。
18×12=216(平方米)
练习2: 小华准备用一根长60米的篱笆围出一块长方形的地用来种菜,如果围成的长方形的长与宽的比是3:2,这块长方形菜地的面积是多少平方米?
回顾与反思:
回顾刚才解决这个问题的过程,想一想,要注意什么?
解答这个问题的时候,我们要注意分清题目中的数量与所给的比的份数之间是否存在对应关系,然后可以转化为分数乘法问题,当然也可以用先求一份数、再求几份数的方法进行解答。
练习3:有三批货物一共值152万元,第一、二、三批货物的质量比是2:4:3,单价的比是6:5:2。第二批货物值多少万元?
(2×6):(4×5):(3×2)
=12:20:6
12+20+6=38
152÷38=4( 万元 )
20×4=80( 万元 )
答:第二批货物值80万元。
巩固练习
练习4:两根同样长的铁条,一根按3:4:5的比锯成三段,另一根按7:9:11的比锯成三段,锯成的铁条有几种不同的长度?
答:有五种不同的长度。
练习5:货车与客车的速度比是4:5,两车同时从甲、乙两站相向行驶,在离中点80千米处相遇。甲、乙两站相距多少千米?
4+5=9
9÷2=4.5
4.5-4=0.5
80÷0.5=160(千米)
160×(4+5)
=160×9
=1440(千米)
答:甲、乙两站相距1440千米。
巩固练习
回顾与总结
应用比解决问题的方法:
一种是用整数法先求一份数,再求出相应的几份数。
另一种是用分数法先求各部分占总数的几分之几,再求各部分数。
解决问题的策略:画图、转化
谢谢!
