初中数学七年级下册北师大 平行线的特征 同步练习(含答案)
文档属性
| 名称 | 初中数学七年级下册北师大 平行线的特征 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 42.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-03 00:00:00 | ||
图片预览


文档简介
平行线的特征同步练习
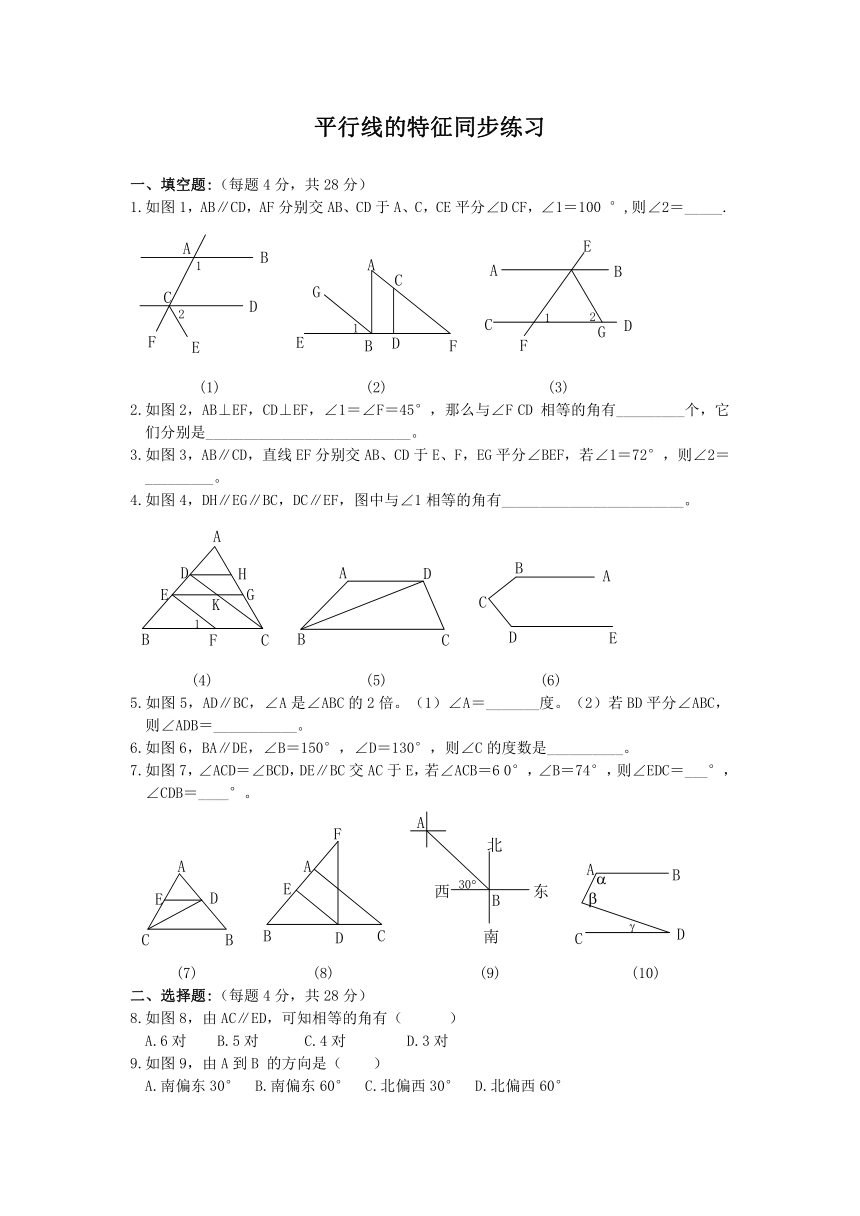
一、填空题:(每题4分,共28分)
1.如图1,AB∥CD,AF分别交AB、CD于A、C,CE平分∠D CF,∠1=100 °,则∠2=_____.毛
(1) (2) (3)
2.如图2,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。
3.如图3,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=_________。
4.如图4,DH∥EG∥BC,DC∥EF,图中与∠1相等的角有________________________。
(4) (5) (6)
5.如图5,AD∥BC,∠A是∠ABC的2倍。(1)∠A=_______度。(2)若BD平分∠ABC,则∠ADB=___________。
6.如图6,BA∥DE,∠B=150°,∠D=130°,则∠C的度数是__________。
7.如图7,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=6 0°,∠B=74°,则∠EDC=___°,∠CDB=____°。
(7) (8) (9) (10)
二、选择题:(每题4分,共28分)
8.如图8,由AC∥ED,可知相等的角有( )
A.6对 B.5对 C.4对 D.3对
9.如图9,由A到B 的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
10.如图10,如果AB∥CD,则角α、β、γ之间的关系为( )
A. α+β+γ=360° B. α-β+γ=180°
C. α+β-γ=180° D. α+β+γ=180°
11.如图11,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=( )
A.60° B.50° C.30° D.20°
(11) (12)
12.下列说法中,为平行线特征的是( )
①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.
A.① B.②③ C.④ D.②和④
13.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )
A.相等 B.互补 C.相等或互补 D.相等且互补
14.如图12,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关系是 ( )
A.是同位角且相等; B.不是同位角但相等; C.是同位角但不等; D.不是同位角也不等
三、解答题:(共44分)
15.已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。(7分)
16.如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME 的度数,(7分)
17.如图,DE∥CB,试证明∠AED=∠A+∠B。(7分)
18.如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?(7)
19.如图,AB∥CD,∠1=∠2,∠BDF与 ∠EFC相等吗?为什么?(8分)
20.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠ AED与∠C的关系。(8分)
参考答案
1. 50° 2. 4,∠F,∠1,∠FAB,∠ABG 3. 54°
4. ∠FEK,∠DCF,∠CKG,∠EKD,∠KDH
5.(1)120°(2)30° 6.80°
7.30°,76°
8.B 9.B 10.C 11.D 12.A 13.C 14.B
15. ∵MN⊥AB,MN⊥CD
∴∠MGB=∠MHD=90°
∴AB∥CD
∴∠EGB=∠EQH
∵∠EQH=180°-∠GQC=180°-120°
=60°
∴∠EGB=60°
∴∠EGM=90°-∠EGB=30°
∴∠EGB=60°,∠HGQ=30°
16. ∵AC∥MD,∠CAB=100°
∴∠CAB+∠AMD=180°,∠AMD=80°
理可得∠EMF=50°
∴∠DME=∠AMB-∠AMD-∠EMB
=180°-80°-50°=50°
17.作EF∥AB交OB于F
∵EF∥AB
∴∠2=∠A,∠3=∠B
∵DE∥CB
∴∠1=∠3
∴∠1=∠B
∴∠1+∠2=∠B+∠A
∴∠AED=∠A+∠B
18. ∵∠2=∠3,∠1=∠2
∴∠1=∠3
∴DB∥EC
∴∠4=∠C
∵∠C=∠D
∴∠D=∠4
∴DF∥AC
∴∠A=∠F
19. ∠BEF=∠EFC,理由如下:
连结BC
∵AB∥CD
∴∠ABC=∠DCB
∵∠1=∠2
∴∠ABC-∠1=∠DCB-∠2
即∠EBC=∠BCF
∴BE∥CF
∴∠BEF=∠EFC
20.∠AED=∠C
∵∠1+∠2=180°
∵∠1+∠4=180°
∴∠2=∠4
∴EF∥AB
∴∠3=∠5
∵∠3=∠B
∴∠5=∠B
∴DE∥BC
∴∠C=∠AED.毛
一、填空题:(每题4分,共28分)
1.如图1,AB∥CD,AF分别交AB、CD于A、C,CE平分∠D CF,∠1=100 °,则∠2=_____.毛
(1) (2) (3)
2.如图2,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。
3.如图3,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=_________。
4.如图4,DH∥EG∥BC,DC∥EF,图中与∠1相等的角有________________________。
(4) (5) (6)
5.如图5,AD∥BC,∠A是∠ABC的2倍。(1)∠A=_______度。(2)若BD平分∠ABC,则∠ADB=___________。
6.如图6,BA∥DE,∠B=150°,∠D=130°,则∠C的度数是__________。
7.如图7,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=6 0°,∠B=74°,则∠EDC=___°,∠CDB=____°。
(7) (8) (9) (10)
二、选择题:(每题4分,共28分)
8.如图8,由AC∥ED,可知相等的角有( )
A.6对 B.5对 C.4对 D.3对
9.如图9,由A到B 的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
10.如图10,如果AB∥CD,则角α、β、γ之间的关系为( )
A. α+β+γ=360° B. α-β+γ=180°
C. α+β-γ=180° D. α+β+γ=180°
11.如图11,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=( )
A.60° B.50° C.30° D.20°
(11) (12)
12.下列说法中,为平行线特征的是( )
①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.
A.① B.②③ C.④ D.②和④
13.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )
A.相等 B.互补 C.相等或互补 D.相等且互补
14.如图12,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关系是 ( )
A.是同位角且相等; B.不是同位角但相等; C.是同位角但不等; D.不是同位角也不等
三、解答题:(共44分)
15.已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。(7分)
16.如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME 的度数,(7分)
17.如图,DE∥CB,试证明∠AED=∠A+∠B。(7分)
18.如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?(7)
19.如图,AB∥CD,∠1=∠2,∠BDF与 ∠EFC相等吗?为什么?(8分)
20.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠ AED与∠C的关系。(8分)
参考答案
1. 50° 2. 4,∠F,∠1,∠FAB,∠ABG 3. 54°
4. ∠FEK,∠DCF,∠CKG,∠EKD,∠KDH
5.(1)120°(2)30° 6.80°
7.30°,76°
8.B 9.B 10.C 11.D 12.A 13.C 14.B
15. ∵MN⊥AB,MN⊥CD
∴∠MGB=∠MHD=90°
∴AB∥CD
∴∠EGB=∠EQH
∵∠EQH=180°-∠GQC=180°-120°
=60°
∴∠EGB=60°
∴∠EGM=90°-∠EGB=30°
∴∠EGB=60°,∠HGQ=30°
16. ∵AC∥MD,∠CAB=100°
∴∠CAB+∠AMD=180°,∠AMD=80°
理可得∠EMF=50°
∴∠DME=∠AMB-∠AMD-∠EMB
=180°-80°-50°=50°
17.作EF∥AB交OB于F
∵EF∥AB
∴∠2=∠A,∠3=∠B
∵DE∥CB
∴∠1=∠3
∴∠1=∠B
∴∠1+∠2=∠B+∠A
∴∠AED=∠A+∠B
18. ∵∠2=∠3,∠1=∠2
∴∠1=∠3
∴DB∥EC
∴∠4=∠C
∵∠C=∠D
∴∠D=∠4
∴DF∥AC
∴∠A=∠F
19. ∠BEF=∠EFC,理由如下:
连结BC
∵AB∥CD
∴∠ABC=∠DCB
∵∠1=∠2
∴∠ABC-∠1=∠DCB-∠2
即∠EBC=∠BCF
∴BE∥CF
∴∠BEF=∠EFC
20.∠AED=∠C
∵∠1+∠2=180°
∵∠1+∠4=180°
∴∠2=∠4
∴EF∥AB
∴∠3=∠5
∵∠3=∠B
∴∠5=∠B
∴DE∥BC
∴∠C=∠AED.毛
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
