7.2.2 解二元一次方程组(2)加减消元法 课件(共23张PPT)
文档属性
| 名称 | 7.2.2 解二元一次方程组(2)加减消元法 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-25 08:26:54 | ||
图片预览








文档简介
(共23张PPT)
7.2.2解二元一次方程组(2)加减消元法
华师大版 七年级 下册
教学目标
教学目标:1.掌握用加减消元法解二元一次方程组.
2.通过探索二元一次方程组的解法,经历化二元一次方程组为
一元一次方程的过程,理解加减消元法的基本思想,体会化
未知为已知的化归思想方法.
教学重点:用加减消元法解二元一次方程组.
教学难点:探索加减消元法解二元一次方程组的过程,感受“消元”思想.
新知导入
情境引入
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含一个未知数的代数式来表示另一个未知数
2、用代入法解方程组的步骤是什么?
1、解二元一次方程组的基本思路是什么?
消元: 二元
一元
一元
复习回顾
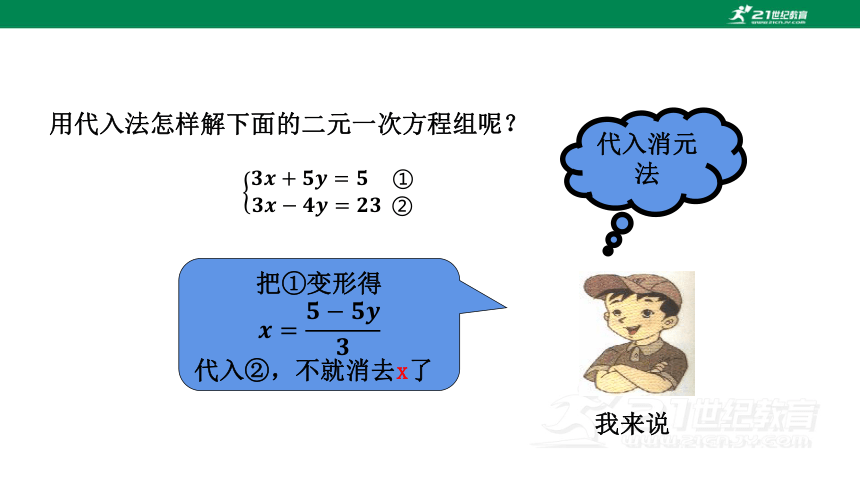
用代入法怎样解下面的二元一次方程组呢?
代入消元法
把①变形得
我来说
代入②,不就消去x了
认真观察此方程组中各个未知数的系数有什么特点,看还有没有其他的解法.并尝试一下能否求出它的解?
把3x看作一个整体
我来说
由①得 3x = 5-5y③
可以将③直接代入②消去3x
还有其他的方法吗
新知讲解
合作学习
例1、解方程组:
如果把这两个方程的左边与左边相减,右边与右边相减,能得到什么结果
分析:
=
①左边
②左边
①右边
②右边
=
左边与左边相减所得到的代数式和右边与右边相减所得到的代数式有什么关系?
提炼概念
对于二元一次方程组,通过将两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程来解的.这种解法叫做加减消元法,简称加减法.
加 减 法
两个二元一次方程中同一个未知数的系数相反或相等
典例精讲
解:由①-②得 (3x+5y)-(3x-4y)=5-23
将y=-2代入①,得 3x+5×(-2)=5
解得 y=-2
解得 x=5
分析:3x与3x相同,因此用①减去②则可消去x
②
①
例1:解方程组:
例2:解方程组:
分析:可以发现7y与-7y互为相反数,若把两个方程的左边与左边相加,右边与右边相加,就可以消去未知数y.
用什么方法可以消去一个未知数 先消去哪一个比较方便
例2、解方程组:
例3:解方程组:
解:①×3,②×2,得
x=6
把x=6代入②,得 30+6y=42
解得 y=2
所以
能否消去x,再求解呢?
解方程组:
解:①×5,②×3,得
y=2
把y=2代入②,得
5x+12=42
解得 x=6
所以
方法二:
归纳概念
在什么情况下,选择用加减消元法解二元一次方程组?体现了什么数学思想?
当方程组中同一未知数的系数相同或相反时,把两个方程相减或相加,消去其中的一个未知数,得到一个一元一次方程.这种解法体现了转化的数学思想.
课堂练习
1.解方程组时,较为简单的方法是( )
A.代入法 B.加减法 C.试值法 D.无法确定
2.用加减法解方程组时,如果消去y,
最简捷的方法是( )
A.①×4-②×3 B.①×4+②×3
C.②×2-① D.②×2+①
B
D
新知讲解
3.如图,嘉嘉和琪琪用不同的方法解方程
组 ,两人求x的过程正确的是( )
A. 嘉嘉正确,琪琪不正确
B. 嘉嘉不正确,琪琪正确
C. 两人都正确
D. 两人都不正确
C
4.解方程组
(1) (2)
(2)
5.已知关于x,y的方程组 .
(1)当a=1时,求方程组的解;
(2)证明:无论a取什么数,x+2y的值始终不变.
解(1)将a=1代入方程组,得
解得
(2)解方程组
得
所以x+2y=2a+1+2(1-a)=2a+1+2-2a=3,
所以,无论a取什么数,x+2y的值始终不变.
课堂总结
基本思路:
二元
一元
加减消元:
1.加减消元法解方程组基本思路是什么?主要步骤有哪些?
主要步骤:
写解
求解
加减
消去一个元
求出两个未知数的值
写出方程组的解
变形
同一个未知数的系数相同或互为相反数
2. 二元一次方程组解法有 .
代入法、加减法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
7.2.2解二元一次方程组(2)加减消元法
华师大版 七年级 下册
教学目标
教学目标:1.掌握用加减消元法解二元一次方程组.
2.通过探索二元一次方程组的解法,经历化二元一次方程组为
一元一次方程的过程,理解加减消元法的基本思想,体会化
未知为已知的化归思想方法.
教学重点:用加减消元法解二元一次方程组.
教学难点:探索加减消元法解二元一次方程组的过程,感受“消元”思想.
新知导入
情境引入
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含一个未知数的代数式来表示另一个未知数
2、用代入法解方程组的步骤是什么?
1、解二元一次方程组的基本思路是什么?
消元: 二元
一元
一元
复习回顾
用代入法怎样解下面的二元一次方程组呢?
代入消元法
把①变形得
我来说
代入②,不就消去x了
认真观察此方程组中各个未知数的系数有什么特点,看还有没有其他的解法.并尝试一下能否求出它的解?
把3x看作一个整体
我来说
由①得 3x = 5-5y③
可以将③直接代入②消去3x
还有其他的方法吗
新知讲解
合作学习
例1、解方程组:
如果把这两个方程的左边与左边相减,右边与右边相减,能得到什么结果
分析:
=
①左边
②左边
①右边
②右边
=
左边与左边相减所得到的代数式和右边与右边相减所得到的代数式有什么关系?
提炼概念
对于二元一次方程组,通过将两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程来解的.这种解法叫做加减消元法,简称加减法.
加 减 法
两个二元一次方程中同一个未知数的系数相反或相等
典例精讲
解:由①-②得 (3x+5y)-(3x-4y)=5-23
将y=-2代入①,得 3x+5×(-2)=5
解得 y=-2
解得 x=5
分析:3x与3x相同,因此用①减去②则可消去x
②
①
例1:解方程组:
例2:解方程组:
分析:可以发现7y与-7y互为相反数,若把两个方程的左边与左边相加,右边与右边相加,就可以消去未知数y.
用什么方法可以消去一个未知数 先消去哪一个比较方便
例2、解方程组:
例3:解方程组:
解:①×3,②×2,得
x=6
把x=6代入②,得 30+6y=42
解得 y=2
所以
能否消去x,再求解呢?
解方程组:
解:①×5,②×3,得
y=2
把y=2代入②,得
5x+12=42
解得 x=6
所以
方法二:
归纳概念
在什么情况下,选择用加减消元法解二元一次方程组?体现了什么数学思想?
当方程组中同一未知数的系数相同或相反时,把两个方程相减或相加,消去其中的一个未知数,得到一个一元一次方程.这种解法体现了转化的数学思想.
课堂练习
1.解方程组时,较为简单的方法是( )
A.代入法 B.加减法 C.试值法 D.无法确定
2.用加减法解方程组时,如果消去y,
最简捷的方法是( )
A.①×4-②×3 B.①×4+②×3
C.②×2-① D.②×2+①
B
D
新知讲解
3.如图,嘉嘉和琪琪用不同的方法解方程
组 ,两人求x的过程正确的是( )
A. 嘉嘉正确,琪琪不正确
B. 嘉嘉不正确,琪琪正确
C. 两人都正确
D. 两人都不正确
C
4.解方程组
(1) (2)
(2)
5.已知关于x,y的方程组 .
(1)当a=1时,求方程组的解;
(2)证明:无论a取什么数,x+2y的值始终不变.
解(1)将a=1代入方程组,得
解得
(2)解方程组
得
所以x+2y=2a+1+2(1-a)=2a+1+2-2a=3,
所以,无论a取什么数,x+2y的值始终不变.
课堂总结
基本思路:
二元
一元
加减消元:
1.加减消元法解方程组基本思路是什么?主要步骤有哪些?
主要步骤:
写解
求解
加减
消去一个元
求出两个未知数的值
写出方程组的解
变形
同一个未知数的系数相同或互为相反数
2. 二元一次方程组解法有 .
代入法、加减法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
