数学人教A版(2019)选择性必修第二册5.3.2导数与极值 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.3.2导数与极值 课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 717.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-25 15:23:31 | ||
图片预览






文档简介
(共15张PPT)
5.3.2导数的极值
1.探索并应用函数极值与导数的关系求函数极值.(重点)
2.利用导数信息判断函数极值的情况.(难点)
学习目标
复习回顾
01
1.导数判断函数单调性
2.已知函数单调性与导数
检验取等
是否成立
知识生成
02
a
t
h
o
最高点
h(t)=-4.9t2+6.5t+10
将最高点附近放大
tt>a
当t=a时,运动员距水面高度最大,
h(t)在此点的导数是多少呢?
单调递增
h′(t)>0
单调递减
h′(t)<0
单调递增
h′(t)>0
单调递减
h′(t)<0
h′(a)=0
2.跳水运动员在最高处附近的情况:
t=a
tt>a
a
t
h
o
最高点
导数的符号有什么变化规律?
在t=a附近,h(t)先增后减,h ′(t)先正后负,h ′(t)连续变化,于是h(a)最大时,有h ′(a)=0.
对于一般函数是否也有同样的性质呢?
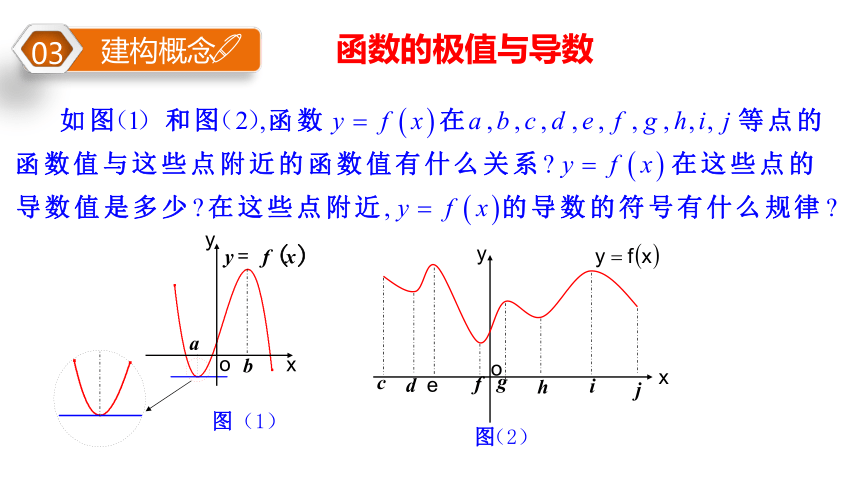
建构概念
03
函数的极值与导数
函数极值的定义:
如果对 附近的所有的点,都有 则 是函数 的一个极小值, 称为极小值点
一般地,设函数 在点 及附近有定义,
如果对 附近的所有的点,都有 则 是函数 的
一个极大值, 称为极大值点
认真观察右图:
① c是极值点吗?
②图中有哪些极值点和极值?
③极大值一定比极小值大吗?
④极大值一定是函数的最大值吗?
1
1.5
2
2.3
3
3.5
结论:
①极值点可以有多个,极大值与极小值之间没有必然的大小关系;
②极值描述的是函数在一个适当区间内的局部性质,不是整体性质,即极值不一定是最值.
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
增
f (x) >0
f (x) =0
f (x) <0
极大值
减
f (x) <0
f (x) =0
增
减
极小值
f (x) >0
请问如何判断f (x0)是极大值或是极小值?
左正右负为极大,右正左负为极小
例1下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
思考:导数值为0的点一定是函数的极值点吗?若是,请说明理由;若不是,你能举一反例吗?
典例研习
04
例2 求函数f(x)=x3-12x+12的极值.
解: =3x2-12=3(x-2)(x+2)
令 =0
得x=2,或x=-2
下面分两种情况讨论:
当 >0即x>2,或x<-2时;
当 <0即-2x (-∞,-2) -2 (-2,2) 2 (2,+∞)
+ 0 - 0 +
f(x) 单调递增↗ 28 单调递减↘ -4 单调递增↗
当x变化时, , f(x)的变化情况如下表;
因此,
当x=-2时,f(x)有极大值,
并且极大值为f(-2)=28
当x=2时,f(x)有极小值,
并且极小值为f(2)=-4
解得
即
归纳小结
一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.
即“峰顶”
即“谷底”
5.3.2导数的极值
1.探索并应用函数极值与导数的关系求函数极值.(重点)
2.利用导数信息判断函数极值的情况.(难点)
学习目标
复习回顾
01
1.导数判断函数单调性
2.已知函数单调性与导数
检验取等
是否成立
知识生成
02
a
t
h
o
最高点
h(t)=-4.9t2+6.5t+10
将最高点附近放大
t
当t=a时,运动员距水面高度最大,
h(t)在此点的导数是多少呢?
单调递增
h′(t)>0
单调递减
h′(t)<0
单调递增
h′(t)>0
单调递减
h′(t)<0
h′(a)=0
2.跳水运动员在最高处附近的情况:
t=a
t
a
t
h
o
最高点
导数的符号有什么变化规律?
在t=a附近,h(t)先增后减,h ′(t)先正后负,h ′(t)连续变化,于是h(a)最大时,有h ′(a)=0.
对于一般函数是否也有同样的性质呢?
建构概念
03
函数的极值与导数
函数极值的定义:
如果对 附近的所有的点,都有 则 是函数 的一个极小值, 称为极小值点
一般地,设函数 在点 及附近有定义,
如果对 附近的所有的点,都有 则 是函数 的
一个极大值, 称为极大值点
认真观察右图:
① c是极值点吗?
②图中有哪些极值点和极值?
③极大值一定比极小值大吗?
④极大值一定是函数的最大值吗?
1
1.5
2
2.3
3
3.5
结论:
①极值点可以有多个,极大值与极小值之间没有必然的大小关系;
②极值描述的是函数在一个适当区间内的局部性质,不是整体性质,即极值不一定是最值.
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
增
f (x) >0
f (x) =0
f (x) <0
极大值
减
f (x) <0
f (x) =0
增
减
极小值
f (x) >0
请问如何判断f (x0)是极大值或是极小值?
左正右负为极大,右正左负为极小
例1下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
思考:导数值为0的点一定是函数的极值点吗?若是,请说明理由;若不是,你能举一反例吗?
典例研习
04
例2 求函数f(x)=x3-12x+12的极值.
解: =3x2-12=3(x-2)(x+2)
令 =0
得x=2,或x=-2
下面分两种情况讨论:
当 >0即x>2,或x<-2时;
当 <0即-2
+ 0 - 0 +
f(x) 单调递增↗ 28 单调递减↘ -4 单调递增↗
当x变化时, , f(x)的变化情况如下表;
因此,
当x=-2时,f(x)有极大值,
并且极大值为f(-2)=28
当x=2时,f(x)有极小值,
并且极小值为f(2)=-4
解得
即
归纳小结
一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.
即“峰顶”
即“谷底”
