数学人教A版(2019)选择性必修第二册5.1.2导数的几何意义 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.1.2导数的几何意义 课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-25 15:25:27 | ||
图片预览






文档简介
(共23张PPT)
5.1.2 导数的几何意义
1.了解平均变化率与割线之间、瞬时变化率与切线之间的关系,通过函数的图象理解导数的几何意义.
2.了解导函数的概念,会求导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.(重点、难点)
平均变化率
一般地,函数 在区间 上的平均变化率为
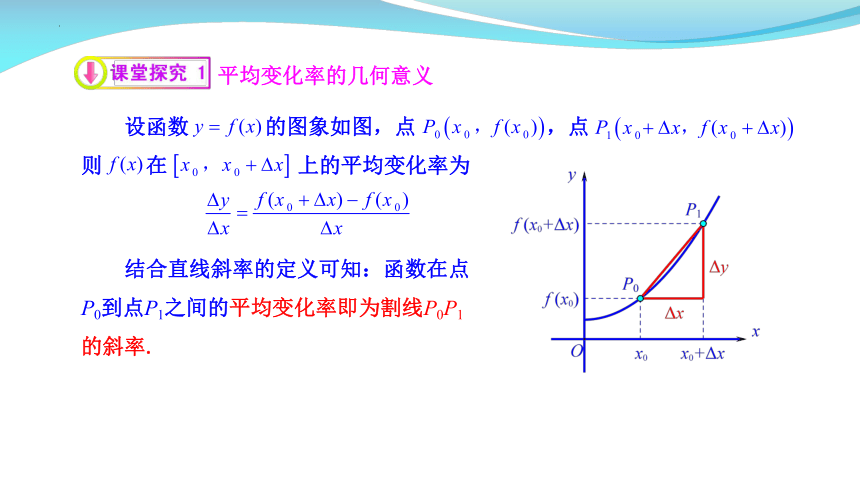
平均变化率的几何意义
设函数 的图象如图,点 ,点 则 在 上的平均变化率为
结合直线斜率的定义可知:函数在点P0到点P1之间的平均变化率即为割线P0P1的斜率.
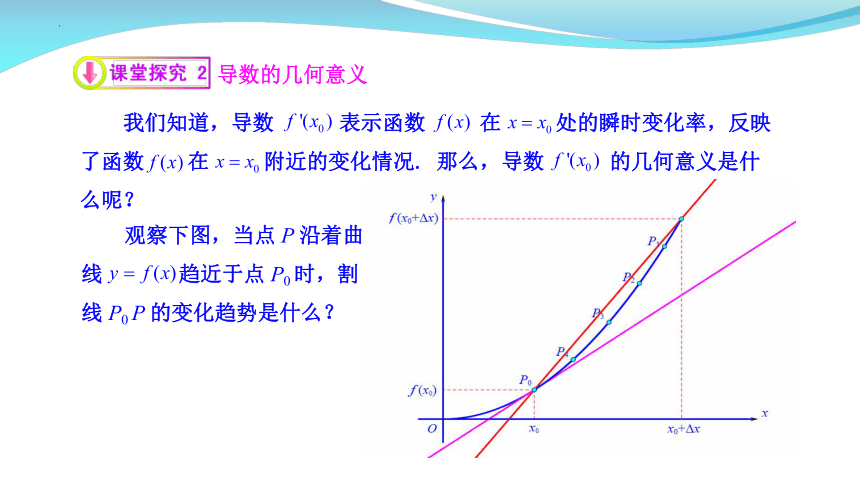
导数的几何意义
我们知道,导数 表示函数 在 处的瞬时变化率,反映了函数 在 附近的变化情况. 那么,导数 的几何意义是什么呢?
观察下图,当点 P 沿着曲线 趋近于点 P0 时,割
线 P0 P 的变化趋势是什么?
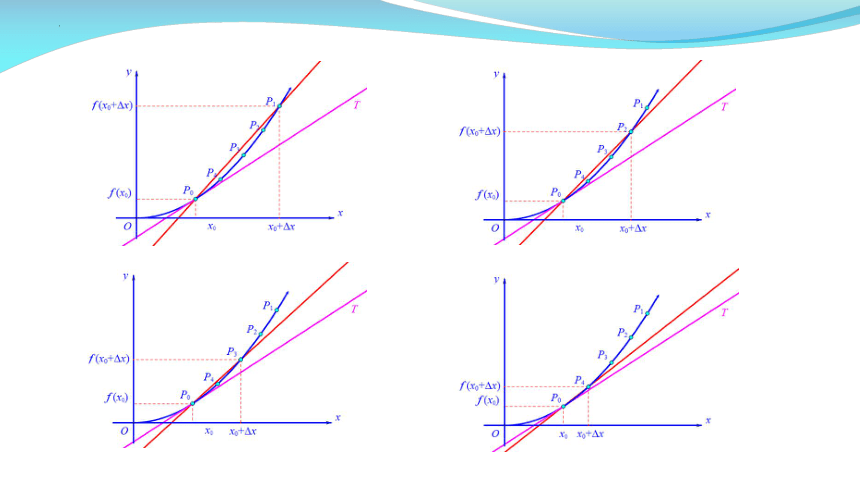
我们发现,当点 P 沿着曲线无限接近点 P 时,即Δx→0时,割线 P0 P趋近于确定的位置,这个确定位置的直线 P0T 称为点 P0处的切线.
容易知道,割线 P0 P 的斜率是
当点 P 无限趋近于点 P0 时,k 无限趋近于切线 P0T 的斜率. 因此,函数
在 处的导数就是切线 P0T 的斜率k,即
1.函数 在 处的导数的几何意义,就是曲线 在点
处的切线的斜率.也即,曲线 在点 处
的切线的斜率是 .
2.曲线 在点 处的切线方程是:
例1.函数 在 处的导数 的几何意义是( )
A.在点 x0 处的斜率
B.在点 处切线与 x 轴所夹锐角的正切值
C.曲线 在点 处切线的斜率
D.点 与点(0,0)连线的斜率
C
导数的几何意义
1.下列命题正确的是( )
A.若 ,则函数 在 处无切线
B.函数 的切线与函数的图象可以有两个公共点
C.函数 在 处的导数
D.曲线 在 处的切线方程为 ,则
B
求曲线的切线
例2.(1)已知曲线 ,求曲线在 处的切线方程;
(2)已知曲线 ,求曲线在 处的切线方程.
解:(1)因为
所以切线方程为
化简得
(2)因为
所以切线方程为
化简得
2.(1)已知曲线 ,求曲线在点 处的切线方程;
(2)已知曲线 ,求曲线过点 的切线方程.
解:(1)因为
所以切线方程为
化简得
解:(2)设切点坐标为 ,因为切点在曲线 上,则 ,
又因为过点 的切线斜率为
因为切线过 和 两点,所以
即 ,解得 或
①当 时,切点为 ,切线为 ;
②当 时,切点为 ,切线为 .
求曲线上的点 P 处的切线与求过点 P 的切线有区别:
(1)在点 P 处的切线,点 P 必为切点;
(2)求过点 P 的切线,点 P 未必是切点,
应注意概念不同,其求法也有所不同.
导函数的定义
从求函数 在 处导数的过程可以看到,当 时, 是一个确定的数.这样,当 x 变化时, 就是 x 的一个函数,我们称它为 的导函数(简称导数). 的导函数有时也记作y',即
函数在某点处的导数与导函数的区别:
(1)函数在某点处的导数是一个定值,导函数是一个函数;
(2)函数 在 x0 处的导数就是导函数 在 处的函数值.
例3.(1)求函数 的导函数;
(2)求函数 的导函数.
解:(1)
(2)
1.已知曲线 上一点A(2,8),则点A处的切线斜率为( )
A.4 B.16 C.8 D.2
C
解:曲线在点A 处切线的斜率就是函数 在 处的导数,
因为
故选C.
2.曲线 在点(-2,-1)处的切线方程为____________.
解:因为
所以切线方程为
化简得
3.设曲线 在点(1,a)处的切线与直线 平行,则 a 等于( )
A.1 B. C. D.
A
解:因为
又切线的斜率为 2,
所以 ,故 .
4.在曲线 上过哪一点的切线.
(1)垂直于直线 ;
(2)与 x 轴成135°的倾斜角.
求切点坐标可以按以下步骤进行:
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
谢谢观看!
5.1.2 导数的几何意义
1.了解平均变化率与割线之间、瞬时变化率与切线之间的关系,通过函数的图象理解导数的几何意义.
2.了解导函数的概念,会求导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.(重点、难点)
平均变化率
一般地,函数 在区间 上的平均变化率为
平均变化率的几何意义
设函数 的图象如图,点 ,点 则 在 上的平均变化率为
结合直线斜率的定义可知:函数在点P0到点P1之间的平均变化率即为割线P0P1的斜率.
导数的几何意义
我们知道,导数 表示函数 在 处的瞬时变化率,反映了函数 在 附近的变化情况. 那么,导数 的几何意义是什么呢?
观察下图,当点 P 沿着曲线 趋近于点 P0 时,割
线 P0 P 的变化趋势是什么?
我们发现,当点 P 沿着曲线无限接近点 P 时,即Δx→0时,割线 P0 P趋近于确定的位置,这个确定位置的直线 P0T 称为点 P0处的切线.
容易知道,割线 P0 P 的斜率是
当点 P 无限趋近于点 P0 时,k 无限趋近于切线 P0T 的斜率. 因此,函数
在 处的导数就是切线 P0T 的斜率k,即
1.函数 在 处的导数的几何意义,就是曲线 在点
处的切线的斜率.也即,曲线 在点 处
的切线的斜率是 .
2.曲线 在点 处的切线方程是:
例1.函数 在 处的导数 的几何意义是( )
A.在点 x0 处的斜率
B.在点 处切线与 x 轴所夹锐角的正切值
C.曲线 在点 处切线的斜率
D.点 与点(0,0)连线的斜率
C
导数的几何意义
1.下列命题正确的是( )
A.若 ,则函数 在 处无切线
B.函数 的切线与函数的图象可以有两个公共点
C.函数 在 处的导数
D.曲线 在 处的切线方程为 ,则
B
求曲线的切线
例2.(1)已知曲线 ,求曲线在 处的切线方程;
(2)已知曲线 ,求曲线在 处的切线方程.
解:(1)因为
所以切线方程为
化简得
(2)因为
所以切线方程为
化简得
2.(1)已知曲线 ,求曲线在点 处的切线方程;
(2)已知曲线 ,求曲线过点 的切线方程.
解:(1)因为
所以切线方程为
化简得
解:(2)设切点坐标为 ,因为切点在曲线 上,则 ,
又因为过点 的切线斜率为
因为切线过 和 两点,所以
即 ,解得 或
①当 时,切点为 ,切线为 ;
②当 时,切点为 ,切线为 .
求曲线上的点 P 处的切线与求过点 P 的切线有区别:
(1)在点 P 处的切线,点 P 必为切点;
(2)求过点 P 的切线,点 P 未必是切点,
应注意概念不同,其求法也有所不同.
导函数的定义
从求函数 在 处导数的过程可以看到,当 时, 是一个确定的数.这样,当 x 变化时, 就是 x 的一个函数,我们称它为 的导函数(简称导数). 的导函数有时也记作y',即
函数在某点处的导数与导函数的区别:
(1)函数在某点处的导数是一个定值,导函数是一个函数;
(2)函数 在 x0 处的导数就是导函数 在 处的函数值.
例3.(1)求函数 的导函数;
(2)求函数 的导函数.
解:(1)
(2)
1.已知曲线 上一点A(2,8),则点A处的切线斜率为( )
A.4 B.16 C.8 D.2
C
解:曲线在点A 处切线的斜率就是函数 在 处的导数,
因为
故选C.
2.曲线 在点(-2,-1)处的切线方程为____________.
解:因为
所以切线方程为
化简得
3.设曲线 在点(1,a)处的切线与直线 平行,则 a 等于( )
A.1 B. C. D.
A
解:因为
又切线的斜率为 2,
所以 ,故 .
4.在曲线 上过哪一点的切线.
(1)垂直于直线 ;
(2)与 x 轴成135°的倾斜角.
求切点坐标可以按以下步骤进行:
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
谢谢观看!
