1.4.2利用空间向量研究距离、夹角问题(2)同步练习(含解析)
文档属性
| 名称 | 1.4.2利用空间向量研究距离、夹角问题(2)同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-26 10:49:38 | ||
图片预览




文档简介
1.4.2利用空间向量研究距离、夹角问题(2)
一、单选题
1. 如图,在棱长为1的正方体中,M,N分别为和的中点,那么直线AM与CN夹角的余弦值为( )
A. B. C. D.
2. 在各棱长均相等的直三棱柱中,已知M是的中点,N是棱AC的中点,则异面直线与BN所成角的正切值为( )
A. B. 1 C. D.
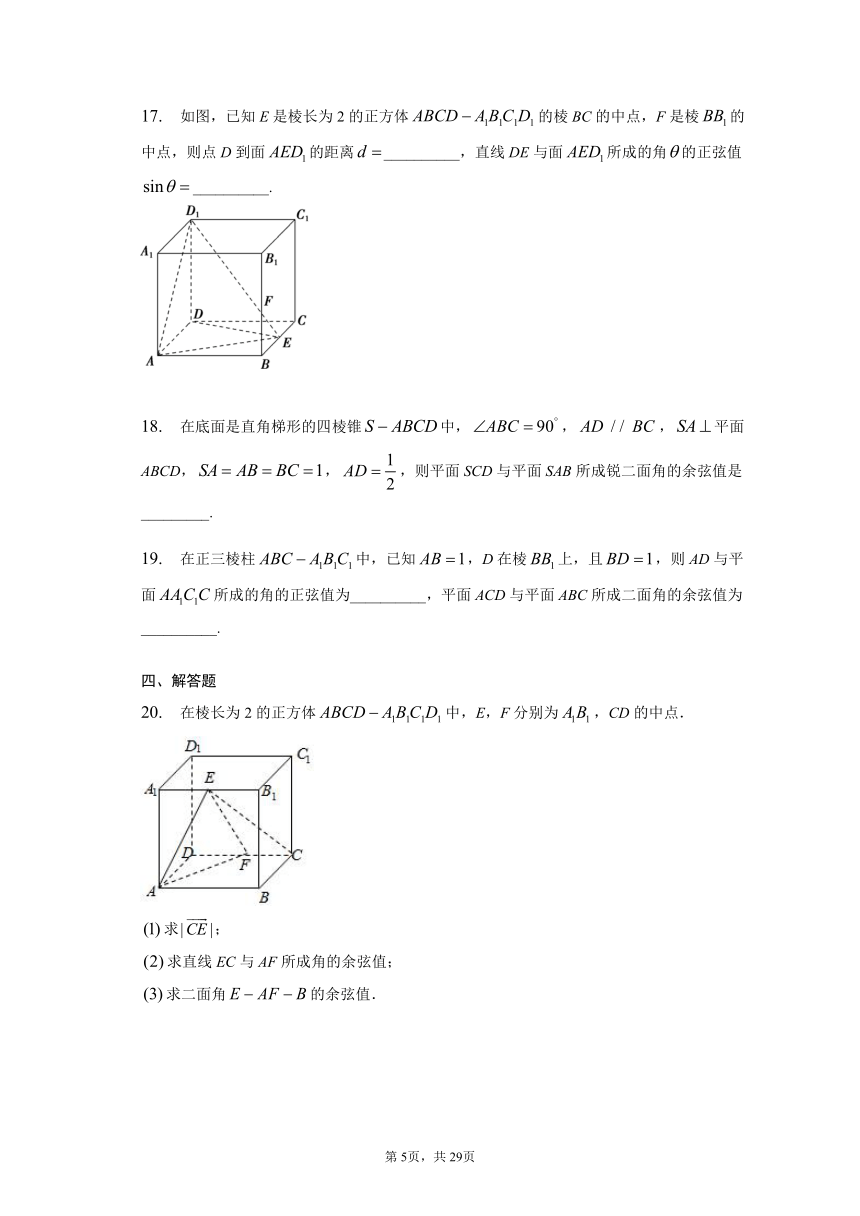
3. 四棱锥中,底面ABCD为直角梯形,,,且,,平面ABCD且,则PB与平面PCD所成角的正弦值为( )
A. B. C. D.
4. 如图,长方体中,,点分别是的中点,则异面直线与GF所成角的余弦值是( )
A. B. C. D. 0
5. 如图,在正方体中,二面角的平面角等于( )
A. B. C. D.
6. 在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑中,平面BCD,,且,M为AD的中点,则二面角的正弦值为( )
A. B. C. D. 1
7. 如图,在三棱锥中,平面平面BCD,与均为等腰直角三角形,且,,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成的角,则线段PA长的取值范围是( )
A. B. C. D.
8. 已知长方体,,,E为线段AB上一点,且,则与平面所成的角的正弦值为( )
A. B. C. D.
9. 如图,在三棱锥中,三条棱DA、DB、DC两两垂直,且,M、N分别是棱BC、AD的中点,则异面直线AM与BN所成角的余弦值为( )
A. B. C. D.
10. 已知三棱柱的侧棱与底面垂直,体积为,底面是边长为的正三角形,若P为底面的中心,则下列选项正确的是( )
A.
B. 直线PA与平面所成角的大小为
C. 异面直线PA与所成角的余弦值为
D. 二面角的正弦值为
二、多选题
11. 如图,在直三棱柱中,,,点D,E分别是线段BC,上的动点不含端点,且则下列说法正确的是( )
A. 平面
B. 该三棱柱的外接球的表面积为
C. 异面直线与所成角的正切值为
D. 二面角的余弦值为
三、填空题
12. 正方体的棱长为2,点M和N分别是和的中点,则异面直线AM和CN所成角的余弦值为__________.
13. 已知正四棱锥的侧棱与底面所成角为,M为PA的中点,连接DM,则DM与平面PAC所成角的大小是___________.
14. 将边长为1的正方形及其内部绕旋转一周形成圆柱,如图,,,其中与C在平面的同侧,则异面直线与所成角的大小是__________.
15. 将边长为a的正方形沿对角线BD折叠成三棱锥,折后,则二面角的余弦值为__________.
16. 如图,在矩形ABCD中,,,E,F分别是边AB,CD的中点,将正方形ADFE沿EF折到位置,使得二面角大小为,则异面直线与CE所成角的余弦值为__________.
17. 如图,已知E是棱长为2的正方体的棱BC的中点,F是棱的中点,则点D到面的距离__________,直线DE与面所成的角的正弦值__________.
18. 在底面是直角梯形的四棱锥中,,,平面ABCD,,,则平面SCD与平面SAB所成锐二面角的余弦值是_________.
19. 在正三棱柱中,已知,D在棱上,且,则AD与平面所成的角的正弦值为__________,平面ACD与平面ABC所成二面角的余弦值为__________.
四、解答题
20. 在棱长为2的正方体中,E,F分别为,CD的中点.
求;
求直线EC与AF所成角的余弦值;
求二面角的余弦值.
如图,在四棱锥中,底面ABCD是平行四边形,,M,N分别为的中点,
证明:;
求直线AN与平面PDM所成角的正弦值.
22. 已知分别是正方体的棱BC和CD的中点,求:
与EF所成角的大小;
与平面所成角的余弦值.
23. 如图,在四棱锥中,面ABCD,,且,,,,,N为PD的中点.
求证:平面
在线段PD上是否存在一点M,使得直线CM与平面PBC所成角的正弦值是,若存在求出的值,若不存在说明理由.
求平面PAD与平面PBC所成二面角的余弦值.
答案和解析
1.【答案】D
解: 设直线AM与CN所成的角为,
在正方体中,,
则
,
所以
故选
2.【答案】C
解:各棱长均相等的直三棱柱中,
设棱长为2,
以A为原点,AC为y轴,为z轴,建立空间直角坐标系,
则,, ,,
,,
设异面直线与BN所成角为,
则,
,
异面直线与BN所成角的正切值为
故选
3.【答案】B
解:依题意,以A为坐标原点,分别以AB,AD,AP
为x,y,z轴建立空间直角坐标系,,,,则,
,,,
从而,,,
设平面PCD的法向量为,
即,
不妨取,则,,
所以平面PCD的一个法向量为,
所以PB与平面PCD所成角的正弦值
,,
故选
4.【答案】D
解:解法一:以DA,DC,所在直线方向为x,y,z轴,建立空间直角坐标系,
则可得,,,,
,,
设异面直线与GF所成角的为,
则,,
解法二:平面,,
,
,
,
,
由勾股定理知,
又,AE、,
平面ABGE,
又平面ABGE,
,
异面直线与GF所成角的余弦值是
故选:
5.【答案】B
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
设正方体中棱长为1,
则,,,
,,
设平面的法向量
则,
取,得,
平面ABD的法向量,
设二面角的平面角为
则,
,
二面角的平面角等于
故选
6.【答案】C
解:取BD的中点N,连接MN,
则平面BCD,
作,H为垂足,连接MH,可知平面MHN,
则,所以是二面角的平面角.
不妨设,根据题意可知
,,
,
故选
7.【答案】B
解:以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,建立空间直角坐标系,
则,,,
设,,
则,
则
,
异面直线PQ与AC成的角,
,
,,
又,,
则,解得,
,
线段PA长的取值范围是
故选:
8.【答案】A
解:以D为原点,DA,DC,为x,y,z轴,建立空间直角坐标系,
则,,,,,
,,,
设平面的一个法向量为,
由,取,得,
与平面所成的角的正弦值为:
故选:
9.【答案】D
解:以D为原点,DB为x轴,DC为y轴,DA为z轴,构造空间直角坐标系,
设,则,,,,
则,,
所以,,
设异面直线与所成角为,
所以,
故选
10.【答案】D
解:如图所示,连接,并延长交于点D,
根据题意,可知:点D为的中点,
底面,
,
,
解得,故A错误;
延长到,使得,连接,则,
分别以,,为x,y,z轴建立空间坐标系,如图,
则,,,,
,,
,,,
为正三角形,P为底面的中心,
,
侧棱与底面垂直,底面,
,
又,、平面,
平面,故为平面的一个法向量,
故直线PA与平面所成角的正弦值为 ;
故直线PA与平面所成角为,故B错误;
异面直线PA与所成角的余弦为 ,故C错误;
设平面ABP的法向量为,
,
,
令,得,
设平面ACP的法向量为,
,
,
令,得,
则
,
则二面角的正弦值为,故D正确.
故选
11.【答案】AD
解:在直三棱柱中,四边形是矩形,
因为,所以,
因为不在平面内,平面,
所以平面,A项正确;
因为,所以,
因为,所以,
所以,
连接,,设其交点为O,连接OA,,,,
由直棱柱的性质知平行四边形是矩形,
,
又平面ABC,平面,
则平面平面,
又平面平面,,
则平面,
又平面,则,
则是直角三角形,又O为的中点,则,
同理,在直角三角形中,,
综上所述,,
则O为直三棱柱外接球的球心,
则是三棱柱外接球的直径,
所以三棱柱外接球的表面积为,所以B项错误;
因为,所以异面直线与所成角为.
在中,,,
所以,所以C项错误;
二面角即二面角,
以A为坐标原点,以,,的方向分别为x,y,z轴的正方向建立空间直角坐标系,
如图,则,
,,,
设平面的法向量,
,即,
令可得;
设平面的一个法向量为,
则,即,
令可得,
故二面角的余弦值为,所以D项正确.
故选
12.【答案】
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
则,,,,
,,
设异面直线AM和CN所成角为,
则
异面直线AM和CN所成角的余弦值为
故答案为:
13.【答案】
解:设底面正方形的边长为a,由已知可得正四棱锥的高为,建立如图所示空间直角坐标系,
则平面PAC的法向量为,,,
,,,
所以〈,〉,
与平面PAC所成角的正弦值为
所以DM与平面PAC所成角为
故答案为
14.【答案】
解:如图所示,建立空间直角坐标系.
,,,
,
,
设异面直线与所成角为
又
所以
故答案为:
15.【答案】
解:取BD中点O,在中,,,
,
,
又是正方形ABCD的对角线,
,
又,平面BCD,平面BCD,
平面BCD,
则OC,OA,OD两两互相垂直,
如图,以O为原点,建立空间直角坐标系,
则,,,
,,
是平面BCD的一个法向量,
,,
设平面ABC的法向量,
则,,
即,
所以,且,
令,则,,
解得,
从而,
易知二面角为锐二面角,
二面角的余弦值为
故答案为
16.【答案】
解:在矩形ABCD中,,,E,F分别是边AB,CD的中点,
将正方形ADFE沿EF折到位置,使得二面角大小为,
以E为原点,在平面中,过E作EB的垂线为x轴,EB为y轴,EF为z轴,建立空间直角坐标系,
,,,,
,,
设异面直线与CE所成角为,
则,
异面直线与CE所成角的余弦值为
故答案为
17.【答案】
解:连接DF,根据正方体的性质,不妨以D点为原点,分别以DA,DC,所在直线为坐标轴建立空间直角坐标系,如下图所示:
由图可知,,,,,,
,,,,
设平面的法向量为,
,
,
取,
,
平面的法向量为,
则
易知与所成角或其补角的余角是直线DE与面所成的角,
,且,
故答案为 .
18.【答案】
解:如图所示,建立空间直角坐标系,
则依题意可知,,,,
可知是平面SAB的一个法向量.
设平面SCD的一个法向量,
因为,,
所以即
令,则有,,所以
设平面SCD与平面SAB所成的锐二面角为,则
故平面SCD与平面SAB所成锐二面角的余弦值是
19.【答案】
解:取AC的中点E,BE为x轴,BE的垂线为y轴,为z轴,建立空间直角坐标系.
在正三棱柱中,,D在棱上,且,
则,,,
正三棱柱中,E为AC中点,
故,且由正三棱柱的性质可得,
而,且AC,平面,
故平面,
故平面的法向量可以为:,
又,
则AD与平面所成的角的正弦值为:
连接DE,因为,,且,BE,平面BDE,
所以平面
又平面BDE,所以
所以是平面ACD与ABC所成二面角的平面角,且为锐角.
在中,,,所以
所以
故答案为:;
20.【答案】解:在棱长为2的正方体中,建立如图所示的空间直角坐标系.
则,,,,,
,,
直线EC与AF所成角的余弦值为
平面ABCD的一个法向量为,
设平面AEF的一个法向量为,
,,
,令,则,,
则
由图知二面角为锐二面角,其余弦值为
21.【答案】解:
证明:
在中,,,,由余弦定理可得,
则,
,
由题意可知,且,
平面PDM,
平面PDM,而,
,又,
由,,而DC与DM相交,平面ABCD,
平面ABCD,
,
,
取AD中点为E,连接ME,则ME,DM,PM两两垂直,以点M为坐标原点,建立空间直角坐标系,如图所示:
则,,,
,,
又N为PC中点,
,,
由得平面PDM,可得可作为平面PDM的一个法向量,
从而直线AN与平面PDM所成角的正弦值为:
22.【答案】解:以分别为轴建立空间直角坐标系,
设正方体的棱长为2a,
则,
所以,
设与EF所成角的大小为,
则
,
因为
所以
所以与EF所成角的大小等于
设平面的法向量为,与平面所成角为,
因为,
所以,
所以,
令得:,,
又因为
所以
,
所以,即与平面所成角的余弦值为
23.【答案】解:过A作于点E,则,以A为原点,AE、AB、AP所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则,,,,,,
为PD的中点,
,,
设平面PBC的法向量为,则,
令,则,,,
,即,
又平面PBC,平面
假设线段PD上存在一点M,设,,,
,,
由知,平面PBC的法向量为,
直线CM与平面PBC所成角的正弦值为,
,
化简得,即,
,,
故
由知,,,
设平面PAD的法向量为,则,
令,则,,,
,
由图可知平面PAD与平面PBC所成二面角为锐角,
故平面PAD与平面PBC所成锐二面角的余弦值为
第32页,共34页
一、单选题
1. 如图,在棱长为1的正方体中,M,N分别为和的中点,那么直线AM与CN夹角的余弦值为( )
A. B. C. D.
2. 在各棱长均相等的直三棱柱中,已知M是的中点,N是棱AC的中点,则异面直线与BN所成角的正切值为( )
A. B. 1 C. D.
3. 四棱锥中,底面ABCD为直角梯形,,,且,,平面ABCD且,则PB与平面PCD所成角的正弦值为( )
A. B. C. D.
4. 如图,长方体中,,点分别是的中点,则异面直线与GF所成角的余弦值是( )
A. B. C. D. 0
5. 如图,在正方体中,二面角的平面角等于( )
A. B. C. D.
6. 在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑中,平面BCD,,且,M为AD的中点,则二面角的正弦值为( )
A. B. C. D. 1
7. 如图,在三棱锥中,平面平面BCD,与均为等腰直角三角形,且,,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成的角,则线段PA长的取值范围是( )
A. B. C. D.
8. 已知长方体,,,E为线段AB上一点,且,则与平面所成的角的正弦值为( )
A. B. C. D.
9. 如图,在三棱锥中,三条棱DA、DB、DC两两垂直,且,M、N分别是棱BC、AD的中点,则异面直线AM与BN所成角的余弦值为( )
A. B. C. D.
10. 已知三棱柱的侧棱与底面垂直,体积为,底面是边长为的正三角形,若P为底面的中心,则下列选项正确的是( )
A.
B. 直线PA与平面所成角的大小为
C. 异面直线PA与所成角的余弦值为
D. 二面角的正弦值为
二、多选题
11. 如图,在直三棱柱中,,,点D,E分别是线段BC,上的动点不含端点,且则下列说法正确的是( )
A. 平面
B. 该三棱柱的外接球的表面积为
C. 异面直线与所成角的正切值为
D. 二面角的余弦值为
三、填空题
12. 正方体的棱长为2,点M和N分别是和的中点,则异面直线AM和CN所成角的余弦值为__________.
13. 已知正四棱锥的侧棱与底面所成角为,M为PA的中点,连接DM,则DM与平面PAC所成角的大小是___________.
14. 将边长为1的正方形及其内部绕旋转一周形成圆柱,如图,,,其中与C在平面的同侧,则异面直线与所成角的大小是__________.
15. 将边长为a的正方形沿对角线BD折叠成三棱锥,折后,则二面角的余弦值为__________.
16. 如图,在矩形ABCD中,,,E,F分别是边AB,CD的中点,将正方形ADFE沿EF折到位置,使得二面角大小为,则异面直线与CE所成角的余弦值为__________.
17. 如图,已知E是棱长为2的正方体的棱BC的中点,F是棱的中点,则点D到面的距离__________,直线DE与面所成的角的正弦值__________.
18. 在底面是直角梯形的四棱锥中,,,平面ABCD,,,则平面SCD与平面SAB所成锐二面角的余弦值是_________.
19. 在正三棱柱中,已知,D在棱上,且,则AD与平面所成的角的正弦值为__________,平面ACD与平面ABC所成二面角的余弦值为__________.
四、解答题
20. 在棱长为2的正方体中,E,F分别为,CD的中点.
求;
求直线EC与AF所成角的余弦值;
求二面角的余弦值.
如图,在四棱锥中,底面ABCD是平行四边形,,M,N分别为的中点,
证明:;
求直线AN与平面PDM所成角的正弦值.
22. 已知分别是正方体的棱BC和CD的中点,求:
与EF所成角的大小;
与平面所成角的余弦值.
23. 如图,在四棱锥中,面ABCD,,且,,,,,N为PD的中点.
求证:平面
在线段PD上是否存在一点M,使得直线CM与平面PBC所成角的正弦值是,若存在求出的值,若不存在说明理由.
求平面PAD与平面PBC所成二面角的余弦值.
答案和解析
1.【答案】D
解: 设直线AM与CN所成的角为,
在正方体中,,
则
,
所以
故选
2.【答案】C
解:各棱长均相等的直三棱柱中,
设棱长为2,
以A为原点,AC为y轴,为z轴,建立空间直角坐标系,
则,, ,,
,,
设异面直线与BN所成角为,
则,
,
异面直线与BN所成角的正切值为
故选
3.【答案】B
解:依题意,以A为坐标原点,分别以AB,AD,AP
为x,y,z轴建立空间直角坐标系,,,,则,
,,,
从而,,,
设平面PCD的法向量为,
即,
不妨取,则,,
所以平面PCD的一个法向量为,
所以PB与平面PCD所成角的正弦值
,,
故选
4.【答案】D
解:解法一:以DA,DC,所在直线方向为x,y,z轴,建立空间直角坐标系,
则可得,,,,
,,
设异面直线与GF所成角的为,
则,,
解法二:平面,,
,
,
,
,
由勾股定理知,
又,AE、,
平面ABGE,
又平面ABGE,
,
异面直线与GF所成角的余弦值是
故选:
5.【答案】B
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
设正方体中棱长为1,
则,,,
,,
设平面的法向量
则,
取,得,
平面ABD的法向量,
设二面角的平面角为
则,
,
二面角的平面角等于
故选
6.【答案】C
解:取BD的中点N,连接MN,
则平面BCD,
作,H为垂足,连接MH,可知平面MHN,
则,所以是二面角的平面角.
不妨设,根据题意可知
,,
,
故选
7.【答案】B
解:以C为原点,CD为x轴,CB为y轴,过C作平面BCD的垂线为z轴,建立空间直角坐标系,
则,,,
设,,
则,
则
,
异面直线PQ与AC成的角,
,
,,
又,,
则,解得,
,
线段PA长的取值范围是
故选:
8.【答案】A
解:以D为原点,DA,DC,为x,y,z轴,建立空间直角坐标系,
则,,,,,
,,,
设平面的一个法向量为,
由,取,得,
与平面所成的角的正弦值为:
故选:
9.【答案】D
解:以D为原点,DB为x轴,DC为y轴,DA为z轴,构造空间直角坐标系,
设,则,,,,
则,,
所以,,
设异面直线与所成角为,
所以,
故选
10.【答案】D
解:如图所示,连接,并延长交于点D,
根据题意,可知:点D为的中点,
底面,
,
,
解得,故A错误;
延长到,使得,连接,则,
分别以,,为x,y,z轴建立空间坐标系,如图,
则,,,,
,,
,,,
为正三角形,P为底面的中心,
,
侧棱与底面垂直,底面,
,
又,、平面,
平面,故为平面的一个法向量,
故直线PA与平面所成角的正弦值为 ;
故直线PA与平面所成角为,故B错误;
异面直线PA与所成角的余弦为 ,故C错误;
设平面ABP的法向量为,
,
,
令,得,
设平面ACP的法向量为,
,
,
令,得,
则
,
则二面角的正弦值为,故D正确.
故选
11.【答案】AD
解:在直三棱柱中,四边形是矩形,
因为,所以,
因为不在平面内,平面,
所以平面,A项正确;
因为,所以,
因为,所以,
所以,
连接,,设其交点为O,连接OA,,,,
由直棱柱的性质知平行四边形是矩形,
,
又平面ABC,平面,
则平面平面,
又平面平面,,
则平面,
又平面,则,
则是直角三角形,又O为的中点,则,
同理,在直角三角形中,,
综上所述,,
则O为直三棱柱外接球的球心,
则是三棱柱外接球的直径,
所以三棱柱外接球的表面积为,所以B项错误;
因为,所以异面直线与所成角为.
在中,,,
所以,所以C项错误;
二面角即二面角,
以A为坐标原点,以,,的方向分别为x,y,z轴的正方向建立空间直角坐标系,
如图,则,
,,,
设平面的法向量,
,即,
令可得;
设平面的一个法向量为,
则,即,
令可得,
故二面角的余弦值为,所以D项正确.
故选
12.【答案】
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
则,,,,
,,
设异面直线AM和CN所成角为,
则
异面直线AM和CN所成角的余弦值为
故答案为:
13.【答案】
解:设底面正方形的边长为a,由已知可得正四棱锥的高为,建立如图所示空间直角坐标系,
则平面PAC的法向量为,,,
,,,
所以〈,〉,
与平面PAC所成角的正弦值为
所以DM与平面PAC所成角为
故答案为
14.【答案】
解:如图所示,建立空间直角坐标系.
,,,
,
,
设异面直线与所成角为
又
所以
故答案为:
15.【答案】
解:取BD中点O,在中,,,
,
,
又是正方形ABCD的对角线,
,
又,平面BCD,平面BCD,
平面BCD,
则OC,OA,OD两两互相垂直,
如图,以O为原点,建立空间直角坐标系,
则,,,
,,
是平面BCD的一个法向量,
,,
设平面ABC的法向量,
则,,
即,
所以,且,
令,则,,
解得,
从而,
易知二面角为锐二面角,
二面角的余弦值为
故答案为
16.【答案】
解:在矩形ABCD中,,,E,F分别是边AB,CD的中点,
将正方形ADFE沿EF折到位置,使得二面角大小为,
以E为原点,在平面中,过E作EB的垂线为x轴,EB为y轴,EF为z轴,建立空间直角坐标系,
,,,,
,,
设异面直线与CE所成角为,
则,
异面直线与CE所成角的余弦值为
故答案为
17.【答案】
解:连接DF,根据正方体的性质,不妨以D点为原点,分别以DA,DC,所在直线为坐标轴建立空间直角坐标系,如下图所示:
由图可知,,,,,,
,,,,
设平面的法向量为,
,
,
取,
,
平面的法向量为,
则
易知与所成角或其补角的余角是直线DE与面所成的角,
,且,
故答案为 .
18.【答案】
解:如图所示,建立空间直角坐标系,
则依题意可知,,,,
可知是平面SAB的一个法向量.
设平面SCD的一个法向量,
因为,,
所以即
令,则有,,所以
设平面SCD与平面SAB所成的锐二面角为,则
故平面SCD与平面SAB所成锐二面角的余弦值是
19.【答案】
解:取AC的中点E,BE为x轴,BE的垂线为y轴,为z轴,建立空间直角坐标系.
在正三棱柱中,,D在棱上,且,
则,,,
正三棱柱中,E为AC中点,
故,且由正三棱柱的性质可得,
而,且AC,平面,
故平面,
故平面的法向量可以为:,
又,
则AD与平面所成的角的正弦值为:
连接DE,因为,,且,BE,平面BDE,
所以平面
又平面BDE,所以
所以是平面ACD与ABC所成二面角的平面角,且为锐角.
在中,,,所以
所以
故答案为:;
20.【答案】解:在棱长为2的正方体中,建立如图所示的空间直角坐标系.
则,,,,,
,,
直线EC与AF所成角的余弦值为
平面ABCD的一个法向量为,
设平面AEF的一个法向量为,
,,
,令,则,,
则
由图知二面角为锐二面角,其余弦值为
21.【答案】解:
证明:
在中,,,,由余弦定理可得,
则,
,
由题意可知,且,
平面PDM,
平面PDM,而,
,又,
由,,而DC与DM相交,平面ABCD,
平面ABCD,
,
,
取AD中点为E,连接ME,则ME,DM,PM两两垂直,以点M为坐标原点,建立空间直角坐标系,如图所示:
则,,,
,,
又N为PC中点,
,,
由得平面PDM,可得可作为平面PDM的一个法向量,
从而直线AN与平面PDM所成角的正弦值为:
22.【答案】解:以分别为轴建立空间直角坐标系,
设正方体的棱长为2a,
则,
所以,
设与EF所成角的大小为,
则
,
因为
所以
所以与EF所成角的大小等于
设平面的法向量为,与平面所成角为,
因为,
所以,
所以,
令得:,,
又因为
所以
,
所以,即与平面所成角的余弦值为
23.【答案】解:过A作于点E,则,以A为原点,AE、AB、AP所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则,,,,,,
为PD的中点,
,,
设平面PBC的法向量为,则,
令,则,,,
,即,
又平面PBC,平面
假设线段PD上存在一点M,设,,,
,,
由知,平面PBC的法向量为,
直线CM与平面PBC所成角的正弦值为,
,
化简得,即,
,,
故
由知,,,
设平面PAD的法向量为,则,
令,则,,,
,
由图可知平面PAD与平面PBC所成二面角为锐角,
故平面PAD与平面PBC所成锐二面角的余弦值为
第32页,共34页
