2022-2023学年沪科版九年级数学下册第25章 投影与视图 单元测试卷(无答案)
文档属性
| 名称 | 2022-2023学年沪科版九年级数学下册第25章 投影与视图 单元测试卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 229.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-26 16:45:11 | ||
图片预览


文档简介
第25章 投影与视图 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 如图所示,从正面看该几何体的图形应为( )
A. B. C. D.
2. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体如图是“牟合方盖”的一种模型,从正面看,所看到的图形是( )
A. B.
C. D.
3. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是( )
A. B. C. D.
4. 如图,是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A. B. C. D.
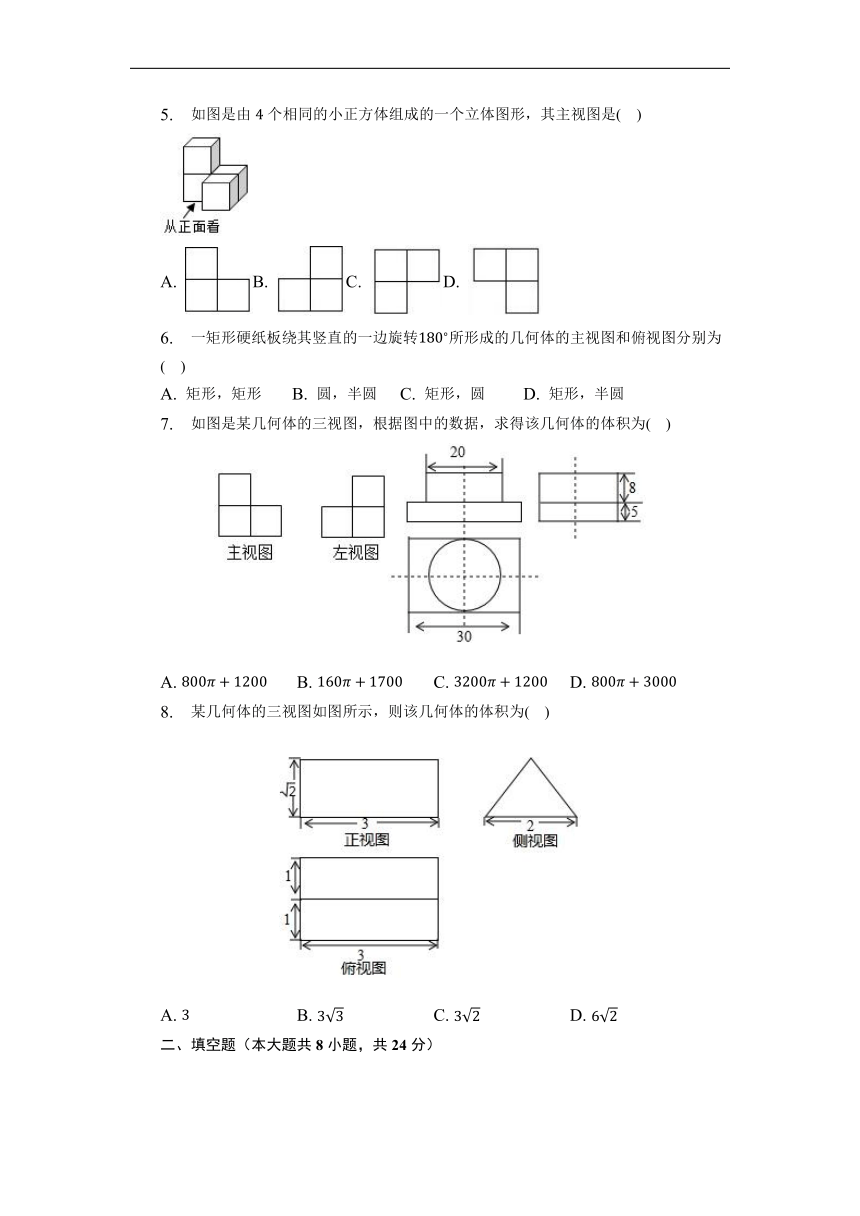
5. 如图是由个相同的小正方体组成的一个立体图形,其主视图是( )
A. B. C. D.
6. 一矩形硬纸板绕其竖直的一边旋转所形成的几何体的主视图和俯视图分别为( )
A. 矩形,矩形 B. 圆,半圆 C. 矩形,圆 D. 矩形,半圆
7. 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A. B. C. D.
8. 某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
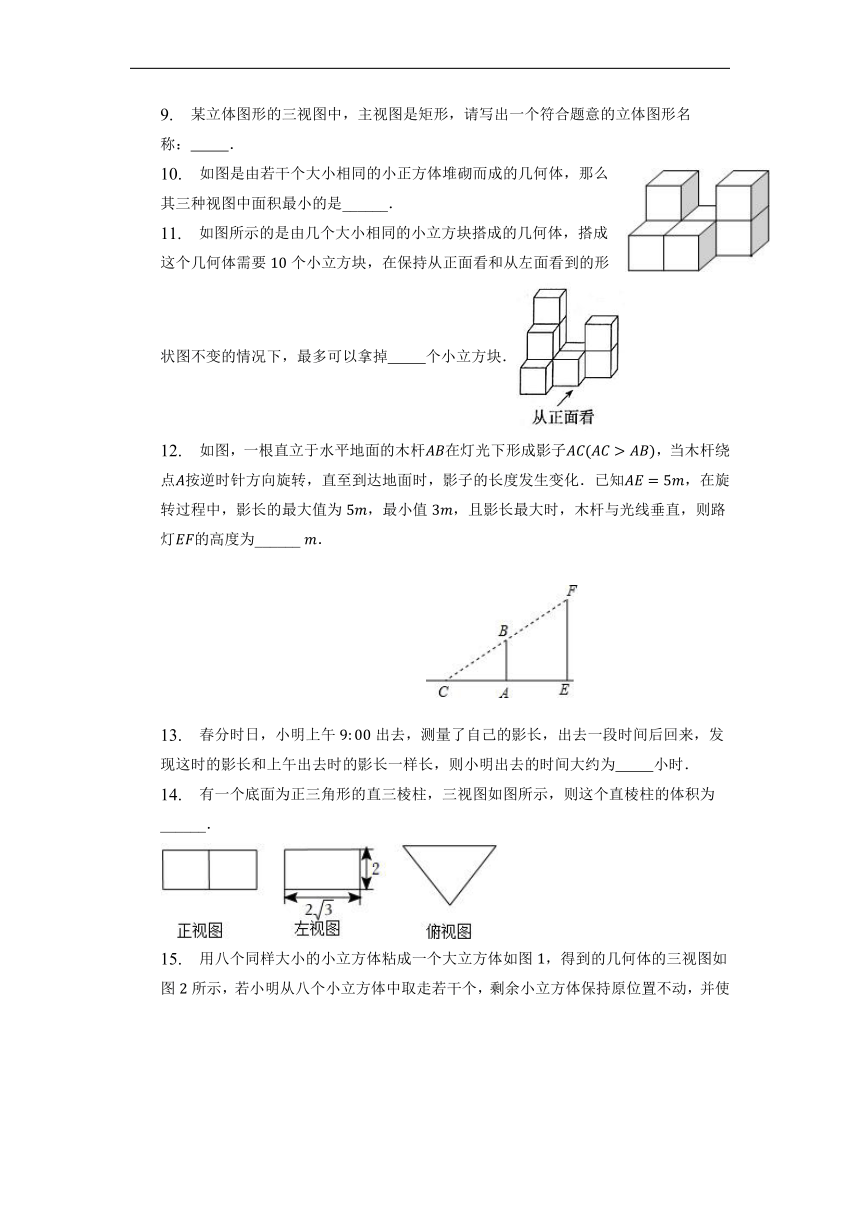
9. 某立体图形的三视图中,主视图是矩形,请写出一个符合题意的立体图形名称: .
10. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______.
11. 如图所示的是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉 个小立方块.
12. 如图,一根直立于水平地面的木杆在灯光下形成影子,当木杆绕点按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知,在旋转过程中,影长的最大值为,最小值,且影长最大时,木杆与光线垂直,则路灯的高度为______ .
13. 春分时日,小明上午出去,测量了自己的影长,出去一段时间后回来,发现这时的影长和上午出去时的影长一样长,则小明出去的时间大约为 小时.
14. 有一个底面为正三角形的直三棱柱,三视图如图所示,则这个直棱柱的体积为______.
15. 用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是________个.
16. 已知某几何体的三视图如图,其中主视图和左视图都是腰长为,底边长为的等腰三角形,则该几何体的侧面展开图的面积是______结果保留
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
纸中画出这个几何体从正面看和从左面看的图形;由几个相同的棱长为的小立方块搭成的几何体从上面看如图所示,方格中的数字表示该位置的小立方块的个数.
在下面方格
求该几何体的表面积.
18. 本小题分
如图,右边正五边形是光线由上到下照射一个正五棱柱正棱柱的上、下底面都是正多边形,并且侧棱垂直于底面时的正投影,你能指出这时正五棱柱的各个面的正投影别是什么吗?
19. 本小题分
把图中的几何体与它们对应的三视图用线连接起来.
20. 本小题分
如图是一个由个相同的小立方块搭成的几何体.
请画出它从三个方向看到的形状图.不需要标序号
将小正方体移走后,所得几何体从三个方向看到的形状图没有发生变化的是______.
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从正面看、从左面看、从上面看
21. 本小题分
如图是一个几何体的三视图图中尺寸单位:,根据图中所示数据计算这个几何体的表面积.
22. 本小题分
如图所示,王华晚上在路灯左侧处时,测得影子的长为米,往右走米到达处时,测得影子的长为米已知王华的身高是米,那么路灯的高度为多少米
23. 本小题分
如图所示,在一个阳光明媚的上午,数学老师组织学生测量小山坡上的一棵大树的高度,山坡与地面的夹角为,站立在水平地面上身高为米的小明在地面上的影长为米,此刻大树在斜坡上的影长为米,求大树的高度.
24. 本小题分
如图所示,点表示广场上的一盏路灯小丽站在距离灯柱米的点处,测得路灯的仰角为,小丽在地面上的影长为,若小丽的身高为米.
求路灯到地面的距离精确到米.
求小丽的影长精确到米参考数据:,,
25. 本小题分
如示意图所示,电灯在以为直径的圆桌面的正上方,以为直径的圆桌面在灯光下的影子是以为直径的圆,,,,点到的距离是,求点到的距离.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 如图所示,从正面看该几何体的图形应为( )
A. B. C. D.
2. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体如图是“牟合方盖”的一种模型,从正面看,所看到的图形是( )
A. B.
C. D.
3. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是( )
A. B. C. D.
4. 如图,是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A. B. C. D.
5. 如图是由个相同的小正方体组成的一个立体图形,其主视图是( )
A. B. C. D.
6. 一矩形硬纸板绕其竖直的一边旋转所形成的几何体的主视图和俯视图分别为( )
A. 矩形,矩形 B. 圆,半圆 C. 矩形,圆 D. 矩形,半圆
7. 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A. B. C. D.
8. 某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
9. 某立体图形的三视图中,主视图是矩形,请写出一个符合题意的立体图形名称: .
10. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______.
11. 如图所示的是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉 个小立方块.
12. 如图,一根直立于水平地面的木杆在灯光下形成影子,当木杆绕点按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知,在旋转过程中,影长的最大值为,最小值,且影长最大时,木杆与光线垂直,则路灯的高度为______ .
13. 春分时日,小明上午出去,测量了自己的影长,出去一段时间后回来,发现这时的影长和上午出去时的影长一样长,则小明出去的时间大约为 小时.
14. 有一个底面为正三角形的直三棱柱,三视图如图所示,则这个直棱柱的体积为______.
15. 用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是________个.
16. 已知某几何体的三视图如图,其中主视图和左视图都是腰长为,底边长为的等腰三角形,则该几何体的侧面展开图的面积是______结果保留
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
纸中画出这个几何体从正面看和从左面看的图形;由几个相同的棱长为的小立方块搭成的几何体从上面看如图所示,方格中的数字表示该位置的小立方块的个数.
在下面方格
求该几何体的表面积.
18. 本小题分
如图,右边正五边形是光线由上到下照射一个正五棱柱正棱柱的上、下底面都是正多边形,并且侧棱垂直于底面时的正投影,你能指出这时正五棱柱的各个面的正投影别是什么吗?
19. 本小题分
把图中的几何体与它们对应的三视图用线连接起来.
20. 本小题分
如图是一个由个相同的小立方块搭成的几何体.
请画出它从三个方向看到的形状图.不需要标序号
将小正方体移走后,所得几何体从三个方向看到的形状图没有发生变化的是______.
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从正面看、从左面看、从上面看
21. 本小题分
如图是一个几何体的三视图图中尺寸单位:,根据图中所示数据计算这个几何体的表面积.
22. 本小题分
如图所示,王华晚上在路灯左侧处时,测得影子的长为米,往右走米到达处时,测得影子的长为米已知王华的身高是米,那么路灯的高度为多少米
23. 本小题分
如图所示,在一个阳光明媚的上午,数学老师组织学生测量小山坡上的一棵大树的高度,山坡与地面的夹角为,站立在水平地面上身高为米的小明在地面上的影长为米,此刻大树在斜坡上的影长为米,求大树的高度.
24. 本小题分
如图所示,点表示广场上的一盏路灯小丽站在距离灯柱米的点处,测得路灯的仰角为,小丽在地面上的影长为,若小丽的身高为米.
求路灯到地面的距离精确到米.
求小丽的影长精确到米参考数据:,,
25. 本小题分
如示意图所示,电灯在以为直径的圆桌面的正上方,以为直径的圆桌面在灯光下的影子是以为直径的圆,,,,点到的距离是,求点到的距离.
