人教版数学七年级上册4.2.1直线、射线、线段 课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.2.1直线、射线、线段 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-26 16:58:55 | ||
图片预览





文档简介
(共19张PPT)
4.2.1直线、射线、线段
趣味时刻:猜谜语
2、大甩卖:新鲜苹果一角一斤(打一数学名词)
1、1加1(打一字)
3、风筝跑了(打一几何)
4、有始无终(打一几何)
5、不走弯路(打一几何)
绝对值
王
线段
射线
直线
情境导入
生活中,有哪些物体可以近似地看成线段、射线、直线?请举例说明
线段
射线
直线
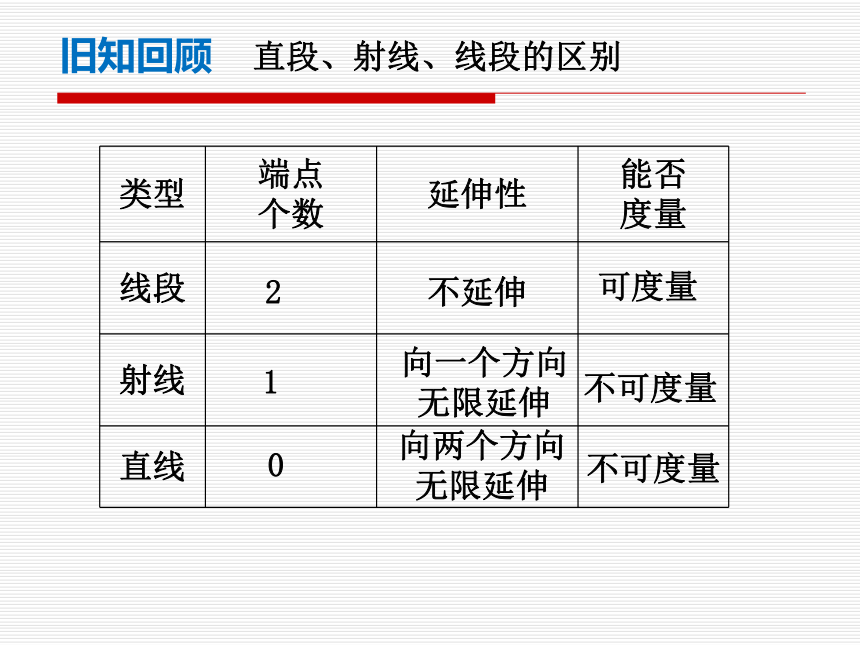
旧知回顾
类型 端点
个数 延伸性 能否
度量
线段
射线
直线
2
不可度量
直段、射线、线段的区别
1
0
不可度量
可度量
不延伸
向一个方向无限延伸
向两个方向无限延伸
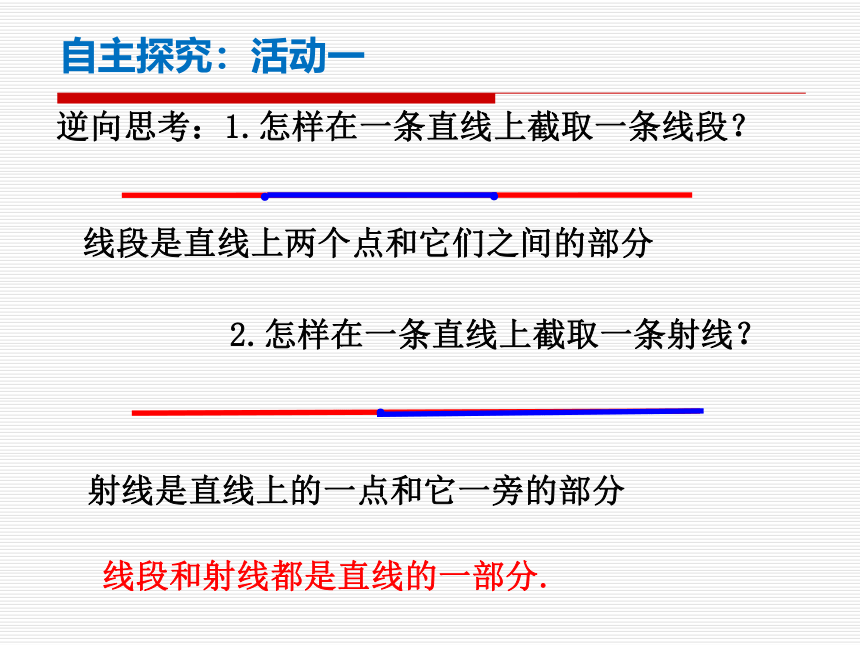
自主探究:活动一
①沪杭高铁/杭沪高铁
②G1301
自主探究:活动一
线段
射 线
线段
直线
A
B
A
B
线段
A
B
①线段AB(线段BA ) ②线段l
①射线AB(射线端点字母要放在前面)
②射线l(不建议使用)
①直线AB(直线BA)
②直线l
延长线段AB (反向延长线段BA )
自主探究:活动一
●
●
●
线段是直线上两个点和它们之间的部分
射线是直线上的一点和它一旁的部分
线段和射线都是直线的一部分.
逆向思考:1.怎样在一条直线上截取一条线段?
2.怎样在一条直线上截取一条射线?
小试牛刀
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
1、判断正误
小试牛刀
2、已知点A、B、C、D,请你快速画: 线段AB,线段AD,射线BC,射线DC,直线AC,
并连接BD
A
B
C
D
●
自主探究:活动二
苏州
问1:该高铁经过嘉兴吗?
问2:该高铁经过苏州吗?
①该高铁经过嘉善
②嘉善在该高铁的线路上
①该高铁不经过苏州
②苏州在该高铁的线路外
直线a经过点O(点O在直线a上)
直线a不经过点P(点P在直线a外)
图形语言
文字语言
●
自主探究:活动二
①点O既在直线m上,又在直线n上
②直线m直线n相交于点O
杭州既在杭温高铁上,又在杭绍台城际铁路上
杭温高铁杭绍台城际铁路相交于点杭州
牛刀小试
1、用适当的语句描述下面的图形
a
b
c
O
c
A
B
C
a
b
2、按语句画图
(2)点A在直线l外;
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点B
(1)直线EF经过点C;
图形语言
文字语言
自主探究:活动三
(1)经过一点A画直线,能画出几条?
A
A
B
(2)经过两点A、B能否画直线?能画出几条呢?
无数条
只有1条
自主探究:活动三
经过两点有一条直线,并且只有一条直线
存在性
唯一性
简单说成:两点确定一条直线
经过思考和画图,可以得到一个基本事实
你能举出一些实际生活中应用“两点确定一条直线”的实例吗?
自主探究
排队
砌墙
种树
射击
课堂小结
谈谈你有哪些收获?
1.这节课所学的基本事实是什么?
2.直线、射线、线段的表示方法?
3.点与直线、直线与直线的位置关系?
我们的现在正处于线段的一端,我们的理想处于线段的另一端。为了实现我们的理想,让我们像射线一样,从现在开始勇往直前,创造像直线一样无限美好地丰富多彩地美丽的人生图案。
寄语
拓展提升
1、当直线a上标出一个点时,可得到 条射线, 条线段;
2、当直线a上标出二个点时,可得到 条射线, 条线段;
3、当直线a上标出三个点时,可得到 条射线, 条线段;
4、当直线a上标出四个点时,可得到 条射线, 条线段;
当直线a上标出n个点时,可得到 条射线, 条线段。
2
0
4
1
6
3
8
6
2n
1.过同一平面上的一个点,可以画______条直线;
1或3
4.过同一平面上的四个点中的任两个点,可以画___ __ _条直线
1或4或6
2.过同一平面上的两个点,可以画______条直线;
3.过同一平面上的三个点中的任两个点,可以画______条直线;
过同一平面上的n个点中的任两个点,
最少可以画______条直线,最多可以画_ _____条直线。
无数
1
1
拓展提升
4.2.1直线、射线、线段
趣味时刻:猜谜语
2、大甩卖:新鲜苹果一角一斤(打一数学名词)
1、1加1(打一字)
3、风筝跑了(打一几何)
4、有始无终(打一几何)
5、不走弯路(打一几何)
绝对值
王
线段
射线
直线
情境导入
生活中,有哪些物体可以近似地看成线段、射线、直线?请举例说明
线段
射线
直线
旧知回顾
类型 端点
个数 延伸性 能否
度量
线段
射线
直线
2
不可度量
直段、射线、线段的区别
1
0
不可度量
可度量
不延伸
向一个方向无限延伸
向两个方向无限延伸
自主探究:活动一
①沪杭高铁/杭沪高铁
②G1301
自主探究:活动一
线段
射 线
线段
直线
A
B
A
B
线段
A
B
①线段AB(线段BA ) ②线段l
①射线AB(射线端点字母要放在前面)
②射线l(不建议使用)
①直线AB(直线BA)
②直线l
延长线段AB (反向延长线段BA )
自主探究:活动一
●
●
●
线段是直线上两个点和它们之间的部分
射线是直线上的一点和它一旁的部分
线段和射线都是直线的一部分.
逆向思考:1.怎样在一条直线上截取一条线段?
2.怎样在一条直线上截取一条射线?
小试牛刀
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
1、判断正误
小试牛刀
2、已知点A、B、C、D,请你快速画: 线段AB,线段AD,射线BC,射线DC,直线AC,
并连接BD
A
B
C
D
●
自主探究:活动二
苏州
问1:该高铁经过嘉兴吗?
问2:该高铁经过苏州吗?
①该高铁经过嘉善
②嘉善在该高铁的线路上
①该高铁不经过苏州
②苏州在该高铁的线路外
直线a经过点O(点O在直线a上)
直线a不经过点P(点P在直线a外)
图形语言
文字语言
●
自主探究:活动二
①点O既在直线m上,又在直线n上
②直线m直线n相交于点O
杭州既在杭温高铁上,又在杭绍台城际铁路上
杭温高铁杭绍台城际铁路相交于点杭州
牛刀小试
1、用适当的语句描述下面的图形
a
b
c
O
c
A
B
C
a
b
2、按语句画图
(2)点A在直线l外;
(3)经过点O的三条线段a、b、c;
(4)线段AB、CD相交于点B
(1)直线EF经过点C;
图形语言
文字语言
自主探究:活动三
(1)经过一点A画直线,能画出几条?
A
A
B
(2)经过两点A、B能否画直线?能画出几条呢?
无数条
只有1条
自主探究:活动三
经过两点有一条直线,并且只有一条直线
存在性
唯一性
简单说成:两点确定一条直线
经过思考和画图,可以得到一个基本事实
你能举出一些实际生活中应用“两点确定一条直线”的实例吗?
自主探究
排队
砌墙
种树
射击
课堂小结
谈谈你有哪些收获?
1.这节课所学的基本事实是什么?
2.直线、射线、线段的表示方法?
3.点与直线、直线与直线的位置关系?
我们的现在正处于线段的一端,我们的理想处于线段的另一端。为了实现我们的理想,让我们像射线一样,从现在开始勇往直前,创造像直线一样无限美好地丰富多彩地美丽的人生图案。
寄语
拓展提升
1、当直线a上标出一个点时,可得到 条射线, 条线段;
2、当直线a上标出二个点时,可得到 条射线, 条线段;
3、当直线a上标出三个点时,可得到 条射线, 条线段;
4、当直线a上标出四个点时,可得到 条射线, 条线段;
当直线a上标出n个点时,可得到 条射线, 条线段。
2
0
4
1
6
3
8
6
2n
1.过同一平面上的一个点,可以画______条直线;
1或3
4.过同一平面上的四个点中的任两个点,可以画___ __ _条直线
1或4或6
2.过同一平面上的两个点,可以画______条直线;
3.过同一平面上的三个点中的任两个点,可以画______条直线;
过同一平面上的n个点中的任两个点,
最少可以画______条直线,最多可以画_ _____条直线。
无数
1
1
拓展提升
