人教版数学八年级上册11.1.1与三角形有关的线段 课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.1.1与三角形有关的线段 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-27 09:06:50 | ||
图片预览


文档简介
(共18张PPT)
11.1.1 与三角形有关的线段
情境导入
有人说,自己步子大,一步能走3米多,你相信吗?
探究1:三角形的有关概念
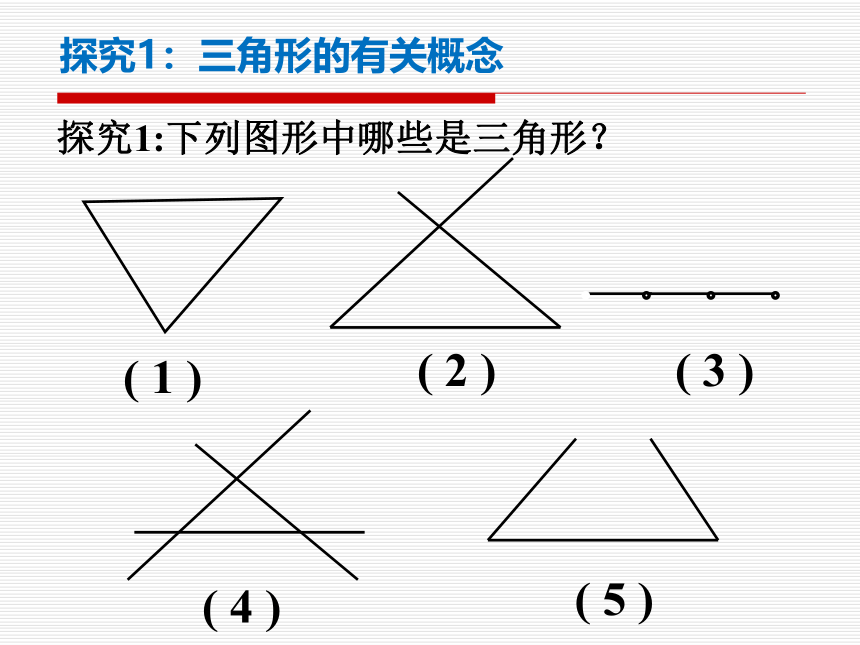
探究1:下列图形中哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
探究1:三角形的有关概念
A
B
C
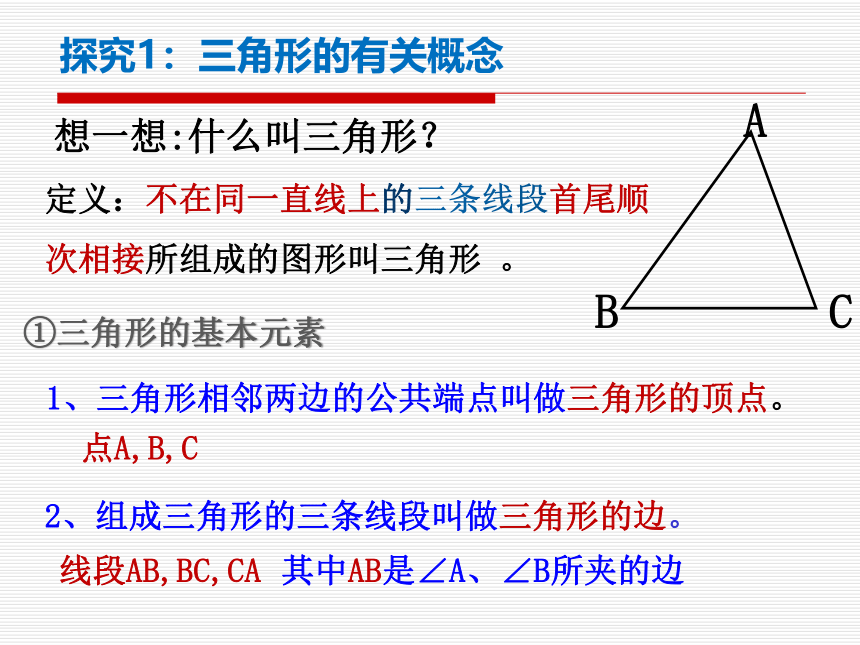
想一想:什么叫三角形?
①三角形的基本元素
1、三角形相邻两边的公共端点叫做三角形的顶点。
2、组成三角形的三条线段叫做三角形的边。
线段AB,BC,CA
点A,B,C
其中AB是∠A、∠B所夹的边
②三角形的表示
A
B
C
用三个顶点字母表示表示为:
读作:三角形ABC
△ABC
探究1:三角形的有关概念
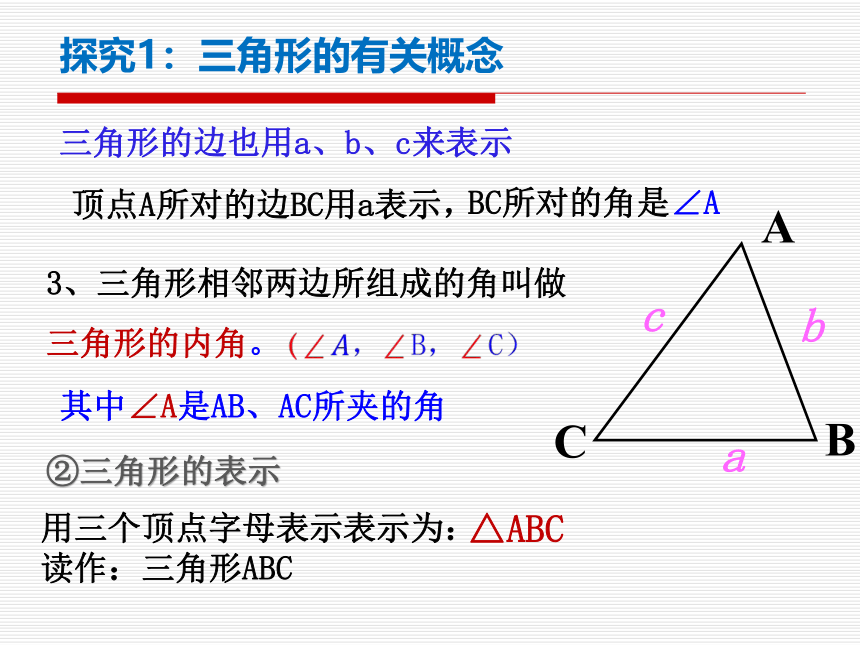
3、三角形相邻两边所组成的角叫做
三角形的内角。
其中∠A是AB、AC所夹的角
BC所对的角是∠A
三角形的边也用a、b、c来表示
顶点A所对的边BC用a表示,
a
c
b
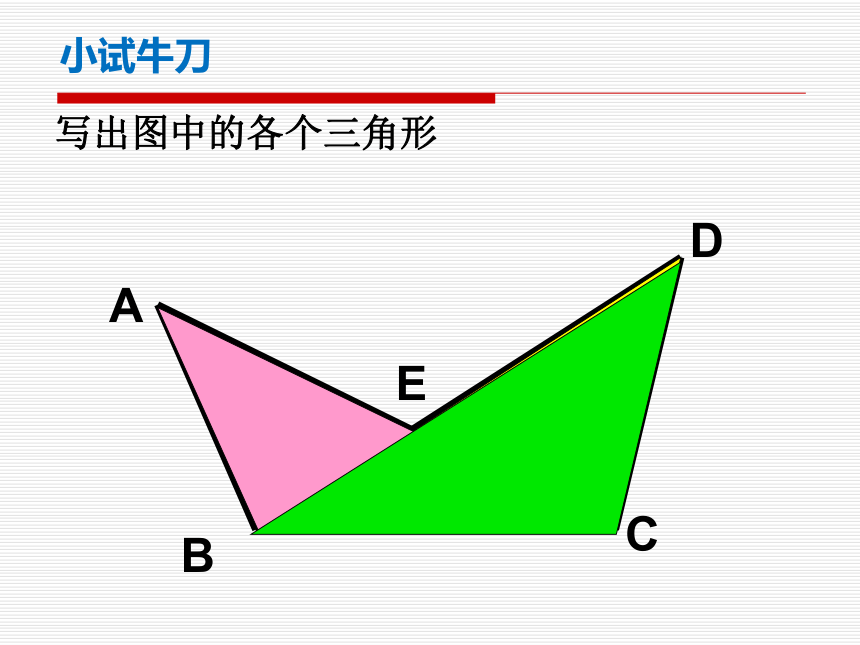
小试牛刀
写出图中的各个三角形
D
B
E
C
A
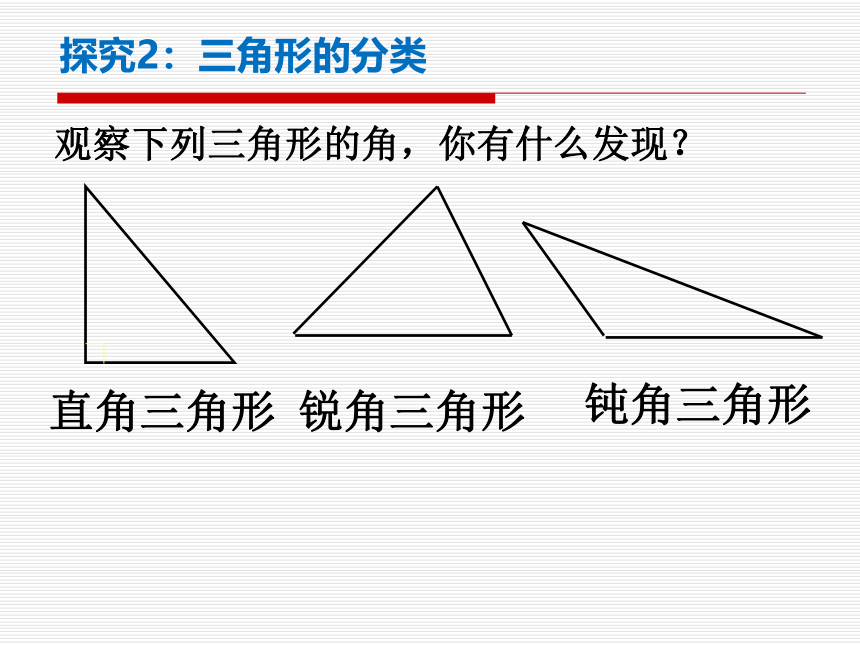
探究2:三角形的分类
观察下列三角形的角,你有什么发现?
直角三角形
锐角三角形
钝角三角形
探究2:三角形的分类
三角形
直角三角形
锐角三角形
钝角三角形
三角形按角分类
探究2:三角形的分类
观察下列三角形的边,你有什么发现?
等腰三角形
等边三角形
等腰三角形
等边三角形是特殊的
等腰三角形
三边都不相等的三角形
等边三角形是特殊的
等腰三角形
探究2:三角形的分类
三角形
三边不相等的三角形
等腰三角形
底和腰不相等
的等腰三角形
等边三角形
三角形按边分类
探究3:三角形的三边关系
如图,送货司机小王要先从椒江出发到临海,再由临海到黄岩,回程时直接从黄岩到椒江,去程与回程路哪个路线线长?
去程路线长是AB+BC.
根据“两点之间,线段最短”
可以得到AB+BC>AC
去程:由点A到点B,
再由点B到点C
回程:由点C到点A
A
C
B
回程路线长是AC.
探究3:三角形的三边关系
同理可得:
AB+AC>BC
AC+BC>AB
AB+BC>AC
变形可得:
AB>BC-AC
AC>AB-BC
AB>AC-BC
1、三角形两边之和大于第三边
2、三角形两边之差小于第三边
牛刀小试
例:下列长度的三条线段能否组成三角形?为什么?
(1) 2,4,5 (2)2,4,6 (3)2,4,7
(4) 5,5,8 (5)5,8,8 (6)5,2,2
追问:判断三条线段能否组成三角形,是否一定要
检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
较小两条线段的和>最长线段
则这三条线段可以构成三角形。
1.若一个三角形的两边长分别为a=4和
b=7,则这个三角形的第三边长c的
范围为_ _ .
3若第三边为奇数,则c =
5、7、9
则这个三角形的周长m的范围为_ _ .
14巩固训练
2.小明有长为2cm,4cm,5cm,7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形?
已知等腰三角形的两边长分别为6cm和11cm,则它的周长为 cm。
23或28
变式1:已知等腰三角形的两边长分别为5cm和11cm,则它的周长为_ ___cm。
27
变式2:一个等腰三角形的周长是36cm,已知其中一边长等于8cm,求其他两边长。
方法点拨:①先分类②再判断
拓展提升
1.已知a,b,c是三角形三边,
试化简:
拓展培优
2.已知a、b、c为△ABC的三边长,满足
(b-2) + ▏c-3 ▏=0,且 a 是方程 ▏a-4 ▏=2的解。求△ABC的周长,并判断△ABC的形状。
课堂小结
三角形
定义
分类
三边
关系
按边分类
按角分类
表示方法
数学思想:分类讨论
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
你会了吗!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。
11.1.1 与三角形有关的线段
情境导入
有人说,自己步子大,一步能走3米多,你相信吗?
探究1:三角形的有关概念
探究1:下列图形中哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
探究1:三角形的有关概念
A
B
C
想一想:什么叫三角形?
①三角形的基本元素
1、三角形相邻两边的公共端点叫做三角形的顶点。
2、组成三角形的三条线段叫做三角形的边。
线段AB,BC,CA
点A,B,C
其中AB是∠A、∠B所夹的边
②三角形的表示
A
B
C
用三个顶点字母表示表示为:
读作:三角形ABC
△ABC
探究1:三角形的有关概念
3、三角形相邻两边所组成的角叫做
三角形的内角。
其中∠A是AB、AC所夹的角
BC所对的角是∠A
三角形的边也用a、b、c来表示
顶点A所对的边BC用a表示,
a
c
b
小试牛刀
写出图中的各个三角形
D
B
E
C
A
探究2:三角形的分类
观察下列三角形的角,你有什么发现?
直角三角形
锐角三角形
钝角三角形
探究2:三角形的分类
三角形
直角三角形
锐角三角形
钝角三角形
三角形按角分类
探究2:三角形的分类
观察下列三角形的边,你有什么发现?
等腰三角形
等边三角形
等腰三角形
等边三角形是特殊的
等腰三角形
三边都不相等的三角形
等边三角形是特殊的
等腰三角形
探究2:三角形的分类
三角形
三边不相等的三角形
等腰三角形
底和腰不相等
的等腰三角形
等边三角形
三角形按边分类
探究3:三角形的三边关系
如图,送货司机小王要先从椒江出发到临海,再由临海到黄岩,回程时直接从黄岩到椒江,去程与回程路哪个路线线长?
去程路线长是AB+BC.
根据“两点之间,线段最短”
可以得到AB+BC>AC
去程:由点A到点B,
再由点B到点C
回程:由点C到点A
A
C
B
回程路线长是AC.
探究3:三角形的三边关系
同理可得:
AB+AC>BC
AC+BC>AB
AB+BC>AC
变形可得:
AB>BC-AC
AC>AB-BC
AB>AC-BC
1、三角形两边之和大于第三边
2、三角形两边之差小于第三边
牛刀小试
例:下列长度的三条线段能否组成三角形?为什么?
(1) 2,4,5 (2)2,4,6 (3)2,4,7
(4) 5,5,8 (5)5,8,8 (6)5,2,2
追问:判断三条线段能否组成三角形,是否一定要
检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
较小两条线段的和>最长线段
则这三条线段可以构成三角形。
1.若一个三角形的两边长分别为a=4和
b=7,则这个三角形的第三边长c的
范围为_ _ .
3
5、7、9
则这个三角形的周长m的范围为_ _ .
14
2.小明有长为2cm,4cm,5cm,7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形?
已知等腰三角形的两边长分别为6cm和11cm,则它的周长为 cm。
23或28
变式1:已知等腰三角形的两边长分别为5cm和11cm,则它的周长为_ ___cm。
27
变式2:一个等腰三角形的周长是36cm,已知其中一边长等于8cm,求其他两边长。
方法点拨:①先分类②再判断
拓展提升
1.已知a,b,c是三角形三边,
试化简:
拓展培优
2.已知a、b、c为△ABC的三边长,满足
(b-2) + ▏c-3 ▏=0,且 a 是方程 ▏a-4 ▏=2的解。求△ABC的周长,并判断△ABC的形状。
课堂小结
三角形
定义
分类
三边
关系
按边分类
按角分类
表示方法
数学思想:分类讨论
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
你会了吗!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。
