山东省威海市乳山一中2014届高三寒假开学检测数学(文)试题
文档属性
| 名称 | 山东省威海市乳山一中2014届高三寒假开学检测数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 11:30:46 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014年高三数学作业检测2.17
(文科)第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,则M∩N= ( )
A. B. C. D.
2.复数,则复数在复平面同偿对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.等差数列中,已知 ( )
A.6 B.5 C.4 D.3
4.过抛物线的焦点作直线交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )
A.2 B.4 C.8 D.16
5.如图1,一个空间几何体的主视图、左视图都是边长为1且一个内角为60°的菱形,俯视图是圆,那么这个几何体的表面积为 ( )
A. B.
C. D.
6.P是所在平面内一点,若,
则P是的( )
A.外心 B.内心
C.重心 D.垂心
7.函数的图象恒过定点A,
且点A在直线上,
则的最小值为 ( )
A.12 B.10 C.8 D.14
8.函数的部分图象如图2所示,则函数表达式为 ( )
A.
B.
C.
D.
9.从分别写有A、B、C、D、E的5张卡片中任取2张,则这2张卡片上的字母恰好是按英文字母表顺序相邻的概率是 ( )
A. B. C. D.
10.函数时,下列式子大小关系正确的是 ( )
A. B.
C. D.
11.数列中,,且,则为 ( )
A. B. C. D.
12.已知是R上的偶函数,若的图象向右平移一个单位后,则得到一个奇函数的图象,则的值为 ( )
A.1 B.0 C.-1 D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分)
13.曲线在点(1,1)处的切线方程为 。
14.若双曲线的一条渐近线方程为,则的值为 。
15.已知正四棱锥S—ABCD,底面上的四个顶点A、B、C、D在球心为O的半球底面圆周上,顶点S在半球面上,则半球O的体积和正四棱锥S—ABCD的体积之比为 。
16.已知函数,则同时满足和0的点所在平面区域的面积是 。
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
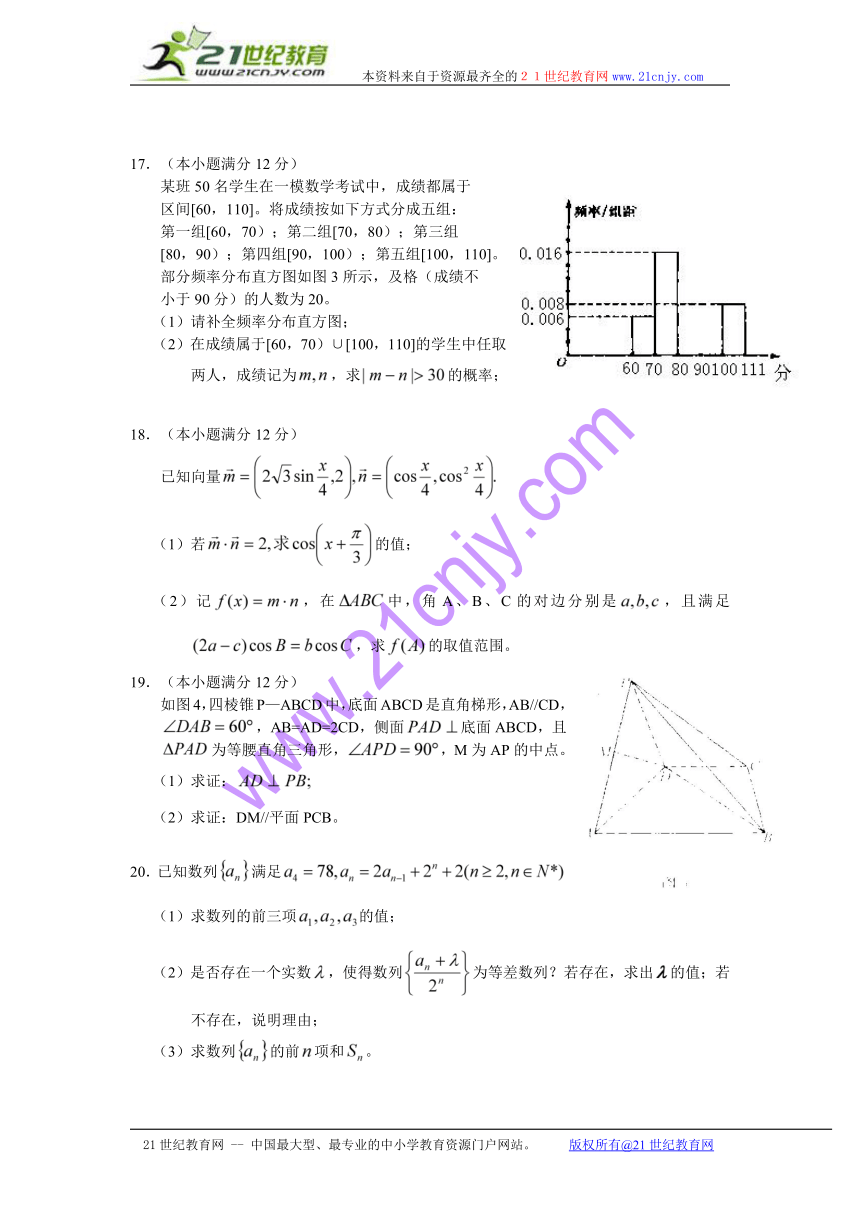
17.(本小题满分12分)
某班50名学生在一模数学考试中,成绩都属于
区间[60,110]。将成绩按如下方式分成五组:
第一组[60,70);第二组[70,80);第三组
[80,90);第四组[90,100);第五组[100,110]。
部分频率分布直方图如图3所示,及格(成绩不
小于90分)的人数为20。
(1)请补全频率分布直方图;
(2)在成绩属于[60,70)∪[100,110]的学生中任取两人,成绩记为,求的概率;
18.(本小题满分12分)
已知向量
(1)若的值;
(2)记,在中,角A、B、C的对边分别是,且满足,求的取值范围。
19.(本小题满分12分)
如图4,四棱锥P—ABCD中,底面ABCD是直角梯形,AB//CD,,AB=AD=2CD,侧面底面ABCD,且为等腰直角三角形,,M为AP的中点。
(1)求证:
(2)求证:DM//平面PCB。
20.已知数列满足
(1)求数列的前三项的值;
(2)是否存在一个实数,使得数列为等差数列?若存在,求出的值;若不存在,说明理由;
(3)求数列的前项和。
21.(本小题满分12分)
已知定点C(-1,0)及椭圆,过点C的动直线与椭圆相交于A,B两点。
(1)若线段AB中点的横坐标是,求直线AB的方程;
(2)在轴上是否存在点M,使为常数?若存在,求出点M的坐标;若不存在,请说明理由。
22.(本小题满分12分)
已知函数
(1)设两曲线与有公共点,且在公共点处的切线相同,若,试建立关于的函数关系式;
(2)在(1)的条件下求的最大值;
(3)若时,函数在(0,4)上为单调函数,求的取值范围。
高三数学作业检测参考答案1.17
一、选择题
1.D; 2.D; 3.A; 4.C; 5.D; 6.D; 7.A; 8.A; 9.B; 10.C; 11.B; 12. B.
二、填空题
13.; 14.; 15.; 16..
三、解答题
17.解:(1)由图得,成绩在的人数为4人,
所以在的人为16人,
所以在的频率为.………2分
在的频率为. ………4分
补全的频率分布直方图如图所示.………6分
(2)由图得:成绩在的有3人,
设为;
在的为4人,设为.
则所取两人总共有:
这21种;………9分
其中满足有这12种
所以的概率为………12分
18.(1)m n==
=2,
∵m n=2,
∴.…………4分
=.…………6分
(2)∵(2a-c)cosB=bcosC,
由正弦定理得,
∴,
∴.∵,
∴,且,∴.…………8分
∴,∴.…………10分
又∵f(x)=m n=2,∴f(A)=2.
故f(A)的取值范围是(2,3).…………12分
19.解: (1)取的中点,连结.
, .………………2分
,且,
是正三角形,,又
平面.
. ……………………6分
(2)取的中点,连结,
分别为的中点,
,且.
∵四边形是直角梯形,且,
且.………………………10分
∴四边形是平行四边形.
.
平面,平面
平面.………………………12分
20.解:(I), ……3分
(II)假设存在一个实数
恒为常数, …………5分
(III)由(II)得,
………………12分
21.解:(1)依题意,直线的斜率存在,设直线的方程为,
将代入, 消去整理得
…………2分
设 因为点(-1,0)在椭圆内部,所以⊿﹥0
则 …………4分
由线段中点的横坐标是, 得,
解得,适合.…………..4分
所以直线的方程为 ,或.………6分
(2)解:
假设在轴上存在点,使为常数.
① 当直线与轴不垂直时,由(Ⅰ)知
所以
…………8分
将代入,整理得
注意到是与无关的常数, 从而有,
此时…………10分
② 当直线与轴垂直时,此时点的坐标分别为,
当时, 亦有………11分
综上,在轴上存在定点,使为常数.………12分
22.解:(1)设与在公共点处的切线相同.
。
由题意知,
即,…………………2分
解得或(舍去),
……………………4分
.
(2)令,则,当变化时,及的变化情况如下表:
所以,时,有最大值. ………………7分
(3)
要使在(0,4)上单调,
须在(0,4)上恒成立.
在(0,4)上恒成立
在(0,4)上恒成立.
而且可为足够小的正数,必有………………9分
或在(0,4)上恒成立
或………………………………11分
综上,所求的取值范围为,或,或.………………12分
A
M
P
B
D
C
G
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014年高三数学作业检测2.17
(文科)第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,则M∩N= ( )
A. B. C. D.
2.复数,则复数在复平面同偿对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.等差数列中,已知 ( )
A.6 B.5 C.4 D.3
4.过抛物线的焦点作直线交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )
A.2 B.4 C.8 D.16
5.如图1,一个空间几何体的主视图、左视图都是边长为1且一个内角为60°的菱形,俯视图是圆,那么这个几何体的表面积为 ( )
A. B.
C. D.
6.P是所在平面内一点,若,
则P是的( )
A.外心 B.内心
C.重心 D.垂心
7.函数的图象恒过定点A,
且点A在直线上,
则的最小值为 ( )
A.12 B.10 C.8 D.14
8.函数的部分图象如图2所示,则函数表达式为 ( )
A.
B.
C.
D.
9.从分别写有A、B、C、D、E的5张卡片中任取2张,则这2张卡片上的字母恰好是按英文字母表顺序相邻的概率是 ( )
A. B. C. D.
10.函数时,下列式子大小关系正确的是 ( )
A. B.
C. D.
11.数列中,,且,则为 ( )
A. B. C. D.
12.已知是R上的偶函数,若的图象向右平移一个单位后,则得到一个奇函数的图象,则的值为 ( )
A.1 B.0 C.-1 D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分)
13.曲线在点(1,1)处的切线方程为 。
14.若双曲线的一条渐近线方程为,则的值为 。
15.已知正四棱锥S—ABCD,底面上的四个顶点A、B、C、D在球心为O的半球底面圆周上,顶点S在半球面上,则半球O的体积和正四棱锥S—ABCD的体积之比为 。
16.已知函数,则同时满足和0的点所在平面区域的面积是 。
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
某班50名学生在一模数学考试中,成绩都属于
区间[60,110]。将成绩按如下方式分成五组:
第一组[60,70);第二组[70,80);第三组
[80,90);第四组[90,100);第五组[100,110]。
部分频率分布直方图如图3所示,及格(成绩不
小于90分)的人数为20。
(1)请补全频率分布直方图;
(2)在成绩属于[60,70)∪[100,110]的学生中任取两人,成绩记为,求的概率;
18.(本小题满分12分)
已知向量
(1)若的值;
(2)记,在中,角A、B、C的对边分别是,且满足,求的取值范围。
19.(本小题满分12分)
如图4,四棱锥P—ABCD中,底面ABCD是直角梯形,AB//CD,,AB=AD=2CD,侧面底面ABCD,且为等腰直角三角形,,M为AP的中点。
(1)求证:
(2)求证:DM//平面PCB。
20.已知数列满足
(1)求数列的前三项的值;
(2)是否存在一个实数,使得数列为等差数列?若存在,求出的值;若不存在,说明理由;
(3)求数列的前项和。
21.(本小题满分12分)
已知定点C(-1,0)及椭圆,过点C的动直线与椭圆相交于A,B两点。
(1)若线段AB中点的横坐标是,求直线AB的方程;
(2)在轴上是否存在点M,使为常数?若存在,求出点M的坐标;若不存在,请说明理由。
22.(本小题满分12分)
已知函数
(1)设两曲线与有公共点,且在公共点处的切线相同,若,试建立关于的函数关系式;
(2)在(1)的条件下求的最大值;
(3)若时,函数在(0,4)上为单调函数,求的取值范围。
高三数学作业检测参考答案1.17
一、选择题
1.D; 2.D; 3.A; 4.C; 5.D; 6.D; 7.A; 8.A; 9.B; 10.C; 11.B; 12. B.
二、填空题
13.; 14.; 15.; 16..
三、解答题
17.解:(1)由图得,成绩在的人数为4人,
所以在的人为16人,
所以在的频率为.………2分
在的频率为. ………4分
补全的频率分布直方图如图所示.………6分
(2)由图得:成绩在的有3人,
设为;
在的为4人,设为.
则所取两人总共有:
这21种;………9分
其中满足有这12种
所以的概率为………12分
18.(1)m n==
=2,
∵m n=2,
∴.…………4分
=.…………6分
(2)∵(2a-c)cosB=bcosC,
由正弦定理得,
∴,
∴.∵,
∴,且,∴.…………8分
∴,∴.…………10分
又∵f(x)=m n=2,∴f(A)=2.
故f(A)的取值范围是(2,3).…………12分
19.解: (1)取的中点,连结.
, .………………2分
,且,
是正三角形,,又
平面.
. ……………………6分
(2)取的中点,连结,
分别为的中点,
,且.
∵四边形是直角梯形,且,
且.………………………10分
∴四边形是平行四边形.
.
平面,平面
平面.………………………12分
20.解:(I), ……3分
(II)假设存在一个实数
恒为常数, …………5分
(III)由(II)得,
………………12分
21.解:(1)依题意,直线的斜率存在,设直线的方程为,
将代入, 消去整理得
…………2分
设 因为点(-1,0)在椭圆内部,所以⊿﹥0
则 …………4分
由线段中点的横坐标是, 得,
解得,适合.…………..4分
所以直线的方程为 ,或.………6分
(2)解:
假设在轴上存在点,使为常数.
① 当直线与轴不垂直时,由(Ⅰ)知
所以
…………8分
将代入,整理得
注意到是与无关的常数, 从而有,
此时…………10分
② 当直线与轴垂直时,此时点的坐标分别为,
当时, 亦有………11分
综上,在轴上存在定点,使为常数.………12分
22.解:(1)设与在公共点处的切线相同.
。
由题意知,
即,…………………2分
解得或(舍去),
……………………4分
.
(2)令,则,当变化时,及的变化情况如下表:
所以,时,有最大值. ………………7分
(3)
要使在(0,4)上单调,
须在(0,4)上恒成立.
在(0,4)上恒成立
在(0,4)上恒成立.
而且可为足够小的正数,必有………………9分
或在(0,4)上恒成立
或………………………………11分
综上,所求的取值范围为,或,或.………………12分
A
M
P
B
D
C
G
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
