2013-2014学年高中数学人教A版选修2-3同步辅导与检测:2.2.3独立重复试验与二项分布
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-3同步辅导与检测:2.2.3独立重复试验与二项分布 |  | |
| 格式 | zip | ||
| 文件大小 | 846.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 12:55:32 | ||
图片预览










文档简介
课件42张PPT。2.2 二项分布及其应用随机变量及其分布2.2.3 独立重复试验与二项分布理解n次独立重复试验的模型及二项分布,并能解答一些简单的实际问题.基础梳理1.所谓独立重复试验,是在同样的条件下________、各次之间________地进行的一种试验,也叫贝努里试验.
特点:每一次试验的结果只有___________________ ___________,且任何一次试验中发生的概率____________.
例如:掷一枚图钉,针尖向上的概率为0.6,则针尖向下的概率为1-0.6=0.4,则第1次、第2次、第3次、…、第n次针尖向上的概率________,这样的试验是___________ ________________.重复地相互独立 两种(某事要么发生,要么不发生)都是一样的相同 独立重复试验(或贝努里试验)2.一般地,在n次独立重复试验中,设事件A发生的次数为X,如果在每次试验中事件A发生的概率是p,那么在n次独立重复试验中事件A恰好发生k次的概率是_____________
___________________.
此时称随机变量X服从________,记作___________,并称p为________概率.
例如:某射手射击1次,击中目标的概率是0.9,他射击4次恰好击中3次的概率是________________________________________________________________________.
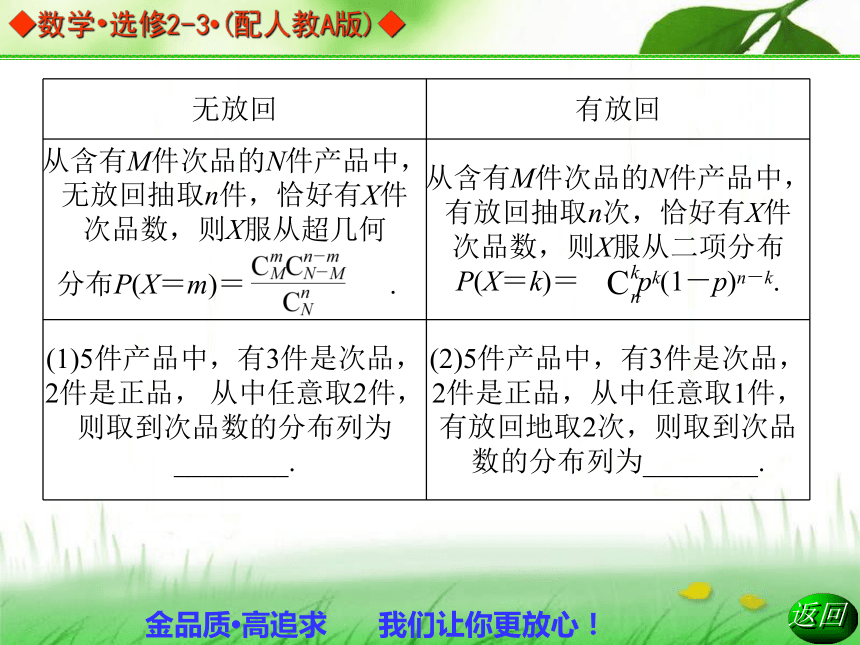
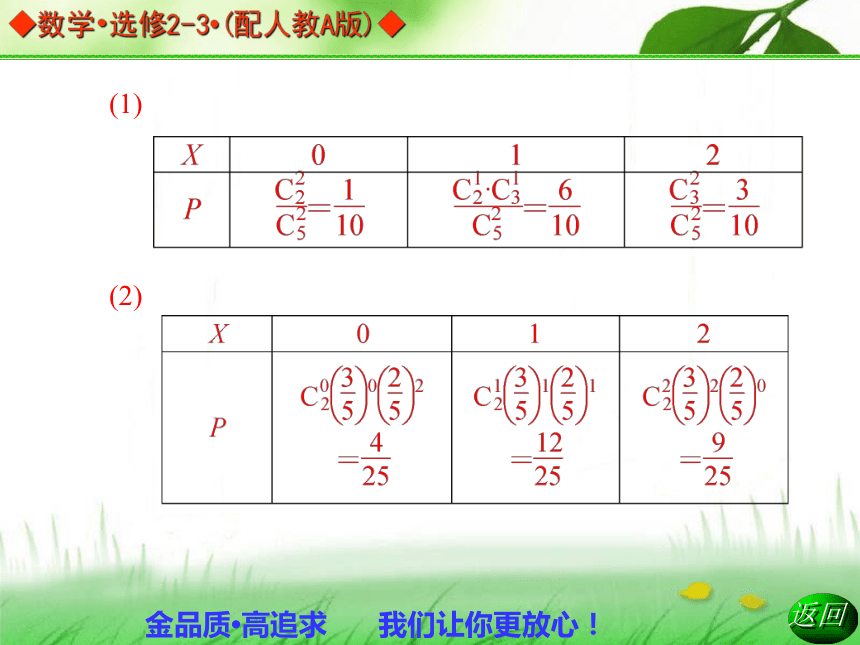
3.有放回与无放回的区别:二项分布X~B(n,p)成功k=0,1,2,···,n分布P(X=m)= .(1)
(2)1.(2011年重点中学联考)有一批蚕豆种子,如果每1粒发育的概率为0.9,播下15粒种子,那么恰有14粒种子发育的概率是( )
A.1-0.914 B.0.914
C. (0.9)×(0.1)14 D. (0.9)4×(0.1)答案:D自测自评A3.已知Y~B ,则P(Y=4)=________.A独立重复试验 某射手进行射击训练,假设每次射击击中目标的概率为 ,且每次射击的结果互不影响,已知射手射击了5次,求:
(1)其中只在第一、三、五次击中目标的概率;
(2)其中恰有3次击中目标的概率;
(3)其中恰有3次连续击中目标,而其他两次没有击中目标的概率.跟踪练习1.某车间的5台机床中的任何一台在1小时内需要工人照管的概率都是 ,求1小时内这5台机床中至少有2台需要工人照管的概率是多少?(结果保留两位有效数字)答案:0.37二项分布 将一枚均匀硬币随机掷100次,求正好出现50次正面的概率.
分析:此题是最简单的试验,每次只有正反两种可能,各次掷出的结果互不影响,故可采用独立重复试验来研究.跟踪练习2.某人参加一次考试,若5道题中解对4道题则为及格.已知他解一道题的正确率为0.6,试求他能及格的概率.
独立重复试验与二项分布的应用 一位病人服用某药品被治愈的概率为90%,求服用这种药的10位患有同样疾病的病人中至少有7人被治愈的概率.
分析:至少有7人被治愈可看成事件A至少发生7次,故由在n次独立重复试验中某事件恰好发生k次的概率计算公式可求.解析:设事件A:“服用此药后病人被治愈”,则有P(A)=90%.
∵10位病人独立地服用此药相当于10次独立重复试验,至少7人被治愈即是事件A至少发生7次.跟踪练习3.一名学生每天骑车上学,从他家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 .
(1)设X为这名学生在途中遇到红灯的次数,求X的概率分布;
(2)设Y为这名学生在首次停车前经过的路口数,求Y的概率分布;
(3)求这名学生在途中至少遇到一次红灯的概率.分析:(1)看作6次独立重复试验.
(2)Y的所有可能取值为0,1,2,3,4,5,6.
(3)至少遇到一次红灯的对立事件是全都是绿灯.所以X的概率分布为:(2)由于Y表示这名学生在首次停车前经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5,6.其中{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.
而{Y=6}表示一路没有遇上红灯,
因此Y的概率分布为:(3)这名学生在途中至少遇到一次红灯的对立事件为该学生在途中没有遇到红灯.
所以其概率为C答案:C3.种植某种树苗,成活率为0.9,若棵的概率约为( )
A.0.33 B.0.66 C.0.5 D.0.45答案:AC6.某射手射击1次,击中目标的概率是0.9,他连续射击4次,且各次射击是否击中目标相互之间没有影响,有下列结论:①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是0.93×0.1;③他至少击中目标1次的概率是1-0.14.其中正确结论的序号是________(写出所有正确结论的序号).①③7.下列事件是独立重复试验的序号是________.
①在一个装有5个红球、5个黑球的袋子中有放回地取球10次,取到红球8次;
②投掷一个骰子5次,点数6向上的次数出现了2次;
③一次抛掷硬币50枚,正面向上的有20枚.①②③8.如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.(1)求p;
(2)求电流能在M与N之间通过的概率.解析:记Ai表示事件:电流能通过Ti,i=1,2,3,4;
A表示事件:T1,T2,T3中至少有一个能通过电流;
B表示事件:电流能在M与N之间通过.9.某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训.已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名下岗人员,求该人参加过培训的概率;
(2)任选3名下岗人员,记X为3人中参加过培训的人数,求X的概率分布.解析:(1)任选1名下岗人员,记“该人参加过财会培训”为事件A,“该人参加过计算机培训”为事件B,由题设知,事件A与B相互独立,且P(A)=0.6,P(B)=0.75.任选1名下岗人员,该人没有参加过培训的概率是
=0.4×0.25=0.1.
所以该人参加过培训的概率是
P2=1-P1=1-0.1=0.9.
(2)因为每个人的选择是相互独立的,
所以3人中参加过培训的人数X服从二项分布B(3,0.9),
P(X=k)= ×0.9k×0.13-k,k=0,1,2,3,
即X的概率分布如下:10.已知一个射手每次击中目标的概率为p= ,求他在4次射击中下列事件发生的概率.
(1)命中一次;
(2)恰在第三次命中目标;
(3)命中两次;
(4)刚好在第二、第三两次击中目标.11.某气象站天气预报的准确率为80%,计算:(结果保留到小数点后面第2位)
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
分析:由于5次预报是相互独立的,且结果只有两种(或准确,或不准确),符合独立重复试验模型.解析:(1)记预报一次准确为事件A,则
P(A)=0.8.5次预报相当于5次独立重复试验,
2次准确的概率为
P= 0.82×0.23=0.051 2≈0.05,
因此5次预报中恰有2次准确的概率为0.05.
(2)“5次预报中至少有2次准确”的对立事件为“5次预报全部不准确或只有1次准确”,其概率为
P= 0.25+C×0.8×0.24
=0.006 72≈0.01.
故所求概率为1-P=1-0.01=0.99.(3)说明第1,2,4,5次中恰有1次准确.
概率为P= 0.8×0.23×0.8=0.020 48≈0.02.
故恰有2次准确,且其中第3次预报准确的概率约为0.02.
点评:解答此类题目的关键在于首先分析随机变量是否满足独立重复试验概型的条件,其次利用P(X=k)=Cpk·(1-p)n-k计算便可.1.对n次独立重复试验的理解
(1)独立重复试验概型有以下特点:
①每次试验是在相同的条件下进行的;
②各次试验的结果不会受其他试验的影响,即每次试验是相互独立的;
③基本事件的概率可知,且每次试验保持不变;
④每次试验只有两种结果,要么发生,要么不发生.2.二项分布与超几何分布的关系
由古典概型得出超几何分布,由独立重复试验概率得出二项分布,这两个分布的关系是:在产品抽样检验中,如果采用有放回抽样,则次品数服从二项分布,如果采用不放回抽样,则次品数服从超几何分布.在实际工作中,抽样一般都采用不放回方式,因此计算次品数为k的概率时应该用超几何分布,但是超几何分布的数值计算涉及总体数目,因此非常繁杂,而二项分布的计算只涉及抽样次数和一个概率值,计算相对简单,并且二项分布的计算可以查专门的数表,所以,当产品总数很大而抽样数不太大时,不放回抽样可以认为是有放回抽样,计算超几何分布可以用计算二项分布来代替.特别提醒:(1)判断一个分布是否为二项分布或超几何分布,其关键是看这个试验是否为独立重复试验.
(2)当从大批产品中抽取少量样品不放回检验时,可以近似地利用二项分布来代替超几何分布.感谢您的使用,退出请按ESC键本小节结束
特点:每一次试验的结果只有___________________ ___________,且任何一次试验中发生的概率____________.
例如:掷一枚图钉,针尖向上的概率为0.6,则针尖向下的概率为1-0.6=0.4,则第1次、第2次、第3次、…、第n次针尖向上的概率________,这样的试验是___________ ________________.重复地相互独立 两种(某事要么发生,要么不发生)都是一样的相同 独立重复试验(或贝努里试验)2.一般地,在n次独立重复试验中,设事件A发生的次数为X,如果在每次试验中事件A发生的概率是p,那么在n次独立重复试验中事件A恰好发生k次的概率是_____________
___________________.
此时称随机变量X服从________,记作___________,并称p为________概率.
例如:某射手射击1次,击中目标的概率是0.9,他射击4次恰好击中3次的概率是________________________________________________________________________.
3.有放回与无放回的区别:二项分布X~B(n,p)成功k=0,1,2,···,n分布P(X=m)= .(1)
(2)1.(2011年重点中学联考)有一批蚕豆种子,如果每1粒发育的概率为0.9,播下15粒种子,那么恰有14粒种子发育的概率是( )
A.1-0.914 B.0.914
C. (0.9)×(0.1)14 D. (0.9)4×(0.1)答案:D自测自评A3.已知Y~B ,则P(Y=4)=________.A独立重复试验 某射手进行射击训练,假设每次射击击中目标的概率为 ,且每次射击的结果互不影响,已知射手射击了5次,求:
(1)其中只在第一、三、五次击中目标的概率;
(2)其中恰有3次击中目标的概率;
(3)其中恰有3次连续击中目标,而其他两次没有击中目标的概率.跟踪练习1.某车间的5台机床中的任何一台在1小时内需要工人照管的概率都是 ,求1小时内这5台机床中至少有2台需要工人照管的概率是多少?(结果保留两位有效数字)答案:0.37二项分布 将一枚均匀硬币随机掷100次,求正好出现50次正面的概率.
分析:此题是最简单的试验,每次只有正反两种可能,各次掷出的结果互不影响,故可采用独立重复试验来研究.跟踪练习2.某人参加一次考试,若5道题中解对4道题则为及格.已知他解一道题的正确率为0.6,试求他能及格的概率.
独立重复试验与二项分布的应用 一位病人服用某药品被治愈的概率为90%,求服用这种药的10位患有同样疾病的病人中至少有7人被治愈的概率.
分析:至少有7人被治愈可看成事件A至少发生7次,故由在n次独立重复试验中某事件恰好发生k次的概率计算公式可求.解析:设事件A:“服用此药后病人被治愈”,则有P(A)=90%.
∵10位病人独立地服用此药相当于10次独立重复试验,至少7人被治愈即是事件A至少发生7次.跟踪练习3.一名学生每天骑车上学,从他家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 .
(1)设X为这名学生在途中遇到红灯的次数,求X的概率分布;
(2)设Y为这名学生在首次停车前经过的路口数,求Y的概率分布;
(3)求这名学生在途中至少遇到一次红灯的概率.分析:(1)看作6次独立重复试验.
(2)Y的所有可能取值为0,1,2,3,4,5,6.
(3)至少遇到一次红灯的对立事件是全都是绿灯.所以X的概率分布为:(2)由于Y表示这名学生在首次停车前经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5,6.其中{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.
而{Y=6}表示一路没有遇上红灯,
因此Y的概率分布为:(3)这名学生在途中至少遇到一次红灯的对立事件为该学生在途中没有遇到红灯.
所以其概率为C答案:C3.种植某种树苗,成活率为0.9,若棵的概率约为( )
A.0.33 B.0.66 C.0.5 D.0.45答案:AC6.某射手射击1次,击中目标的概率是0.9,他连续射击4次,且各次射击是否击中目标相互之间没有影响,有下列结论:①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是0.93×0.1;③他至少击中目标1次的概率是1-0.14.其中正确结论的序号是________(写出所有正确结论的序号).①③7.下列事件是独立重复试验的序号是________.
①在一个装有5个红球、5个黑球的袋子中有放回地取球10次,取到红球8次;
②投掷一个骰子5次,点数6向上的次数出现了2次;
③一次抛掷硬币50枚,正面向上的有20枚.①②③8.如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.(1)求p;
(2)求电流能在M与N之间通过的概率.解析:记Ai表示事件:电流能通过Ti,i=1,2,3,4;
A表示事件:T1,T2,T3中至少有一个能通过电流;
B表示事件:电流能在M与N之间通过.9.某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训.已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名下岗人员,求该人参加过培训的概率;
(2)任选3名下岗人员,记X为3人中参加过培训的人数,求X的概率分布.解析:(1)任选1名下岗人员,记“该人参加过财会培训”为事件A,“该人参加过计算机培训”为事件B,由题设知,事件A与B相互独立,且P(A)=0.6,P(B)=0.75.任选1名下岗人员,该人没有参加过培训的概率是
=0.4×0.25=0.1.
所以该人参加过培训的概率是
P2=1-P1=1-0.1=0.9.
(2)因为每个人的选择是相互独立的,
所以3人中参加过培训的人数X服从二项分布B(3,0.9),
P(X=k)= ×0.9k×0.13-k,k=0,1,2,3,
即X的概率分布如下:10.已知一个射手每次击中目标的概率为p= ,求他在4次射击中下列事件发生的概率.
(1)命中一次;
(2)恰在第三次命中目标;
(3)命中两次;
(4)刚好在第二、第三两次击中目标.11.某气象站天气预报的准确率为80%,计算:(结果保留到小数点后面第2位)
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
分析:由于5次预报是相互独立的,且结果只有两种(或准确,或不准确),符合独立重复试验模型.解析:(1)记预报一次准确为事件A,则
P(A)=0.8.5次预报相当于5次独立重复试验,
2次准确的概率为
P= 0.82×0.23=0.051 2≈0.05,
因此5次预报中恰有2次准确的概率为0.05.
(2)“5次预报中至少有2次准确”的对立事件为“5次预报全部不准确或只有1次准确”,其概率为
P= 0.25+C×0.8×0.24
=0.006 72≈0.01.
故所求概率为1-P=1-0.01=0.99.(3)说明第1,2,4,5次中恰有1次准确.
概率为P= 0.8×0.23×0.8=0.020 48≈0.02.
故恰有2次准确,且其中第3次预报准确的概率约为0.02.
点评:解答此类题目的关键在于首先分析随机变量是否满足独立重复试验概型的条件,其次利用P(X=k)=Cpk·(1-p)n-k计算便可.1.对n次独立重复试验的理解
(1)独立重复试验概型有以下特点:
①每次试验是在相同的条件下进行的;
②各次试验的结果不会受其他试验的影响,即每次试验是相互独立的;
③基本事件的概率可知,且每次试验保持不变;
④每次试验只有两种结果,要么发生,要么不发生.2.二项分布与超几何分布的关系
由古典概型得出超几何分布,由独立重复试验概率得出二项分布,这两个分布的关系是:在产品抽样检验中,如果采用有放回抽样,则次品数服从二项分布,如果采用不放回抽样,则次品数服从超几何分布.在实际工作中,抽样一般都采用不放回方式,因此计算次品数为k的概率时应该用超几何分布,但是超几何分布的数值计算涉及总体数目,因此非常繁杂,而二项分布的计算只涉及抽样次数和一个概率值,计算相对简单,并且二项分布的计算可以查专门的数表,所以,当产品总数很大而抽样数不太大时,不放回抽样可以认为是有放回抽样,计算超几何分布可以用计算二项分布来代替.特别提醒:(1)判断一个分布是否为二项分布或超几何分布,其关键是看这个试验是否为独立重复试验.
(2)当从大批产品中抽取少量样品不放回检验时,可以近似地利用二项分布来代替超几何分布.感谢您的使用,退出请按ESC键本小节结束
